隐马尔可夫随机场HMM
概率知识点:
0=<P(A)<=1
P(True)=1;P(False)=0
P(A)+P(B)-P(A and B) = P(A or B)
P(A|B)=P(A,B)/P(B)
=> P(A,B)=P(A|B)P(B)
=>P(A,B,C) = P(A|B,C)P(B|C)P(C)
如果A,B 相互独立,P(A,B) = P(A)P(B) =>P(A|B)=P(A)
朴素贝叶斯 :
P(y=1|x1,x2,……xn)=P(x1,……xn|y=1)p(y=1)/p(x1,……xn)
马尔可夫模型:
X1->X2->X3->X4----->
P(X1,……Xn)=P(X1)P(X2|X1)……P(Xn|Xn-1)
马尔可夫矩阵具有无记
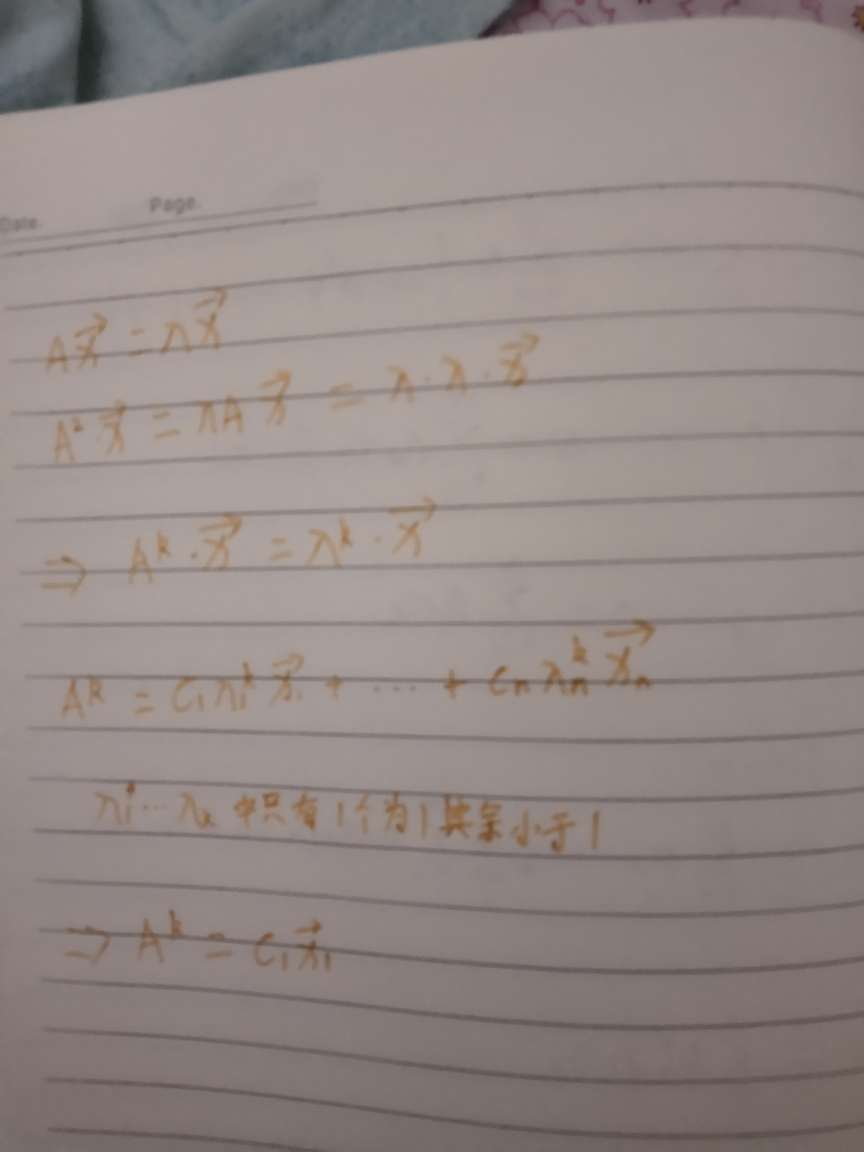
X1->X2->X3
| | |
Y1 Y2 Y3
目标函数:
P(Xt|Y1:t) = P(Xt|Y1……Yt)
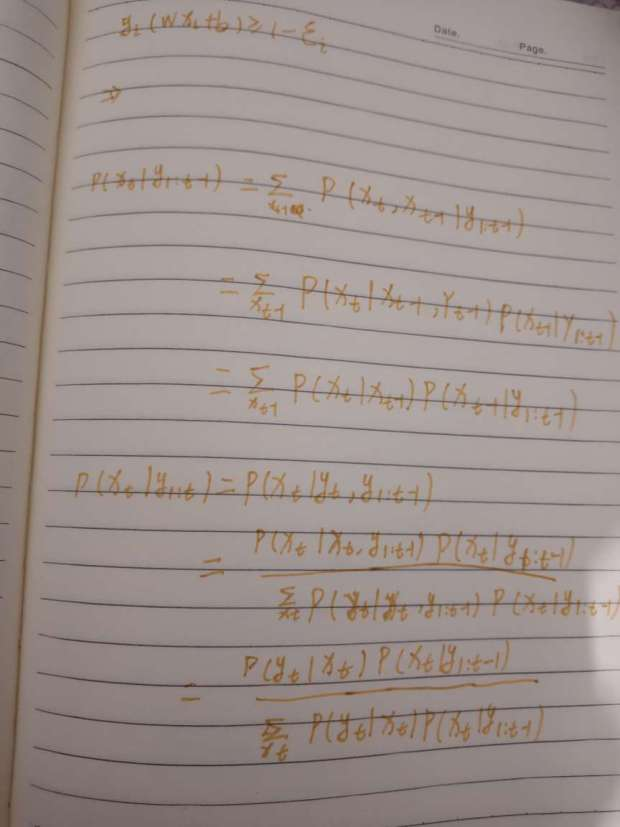
隐马尔可夫随机场HMM的更多相关文章
- 隐马尔科夫模型 HMM(Hidden Markov Model)
本科阶段学了三四遍的HMM,机器学习课,自然语言处理课,中文信息处理课:如今学研究生的自然语言处理,又碰见了这个老熟人: 虽多次碰到,但总觉得一知半解,对其了解不够全面,借着这次的机会,我想要直接搞定 ...
- 基于隐马尔科夫模型(HMM)的地图匹配(Map-Matching)算法
文章目录 1. 1. 摘要 2. 2. Map-Matching(MM)问题 3. 3. 隐马尔科夫模型(HMM) 3.1. 3.1. HMM简述 3.2. 3.2. 基于HMM的Map-Matchi ...
- 通俗理解隐马尔科夫模型HMM(转载)
作者:Yang Eninala 链接:https://www.zhihu.com/question/20962240/answer/33438846 来源:知乎 著作权归作者所有,转载请联系作者获得授 ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 猪猪的机器学习笔记(十七)隐马尔科夫模型HMM
隐马尔科夫模型HMM 作者:樱花猪 摘要: 本文为七月算法(julyedu.com)12月机器学习第十七次课在线笔记.隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来 ...
- 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(一)HMM模型
隐马尔科夫模型HMM(一)HMM模型基础 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比 ...
- 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态序列
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态 ...
随机推荐
- 十分简明易懂的FFT(快速傅里叶变换)
https://blog.csdn.net/enjoy_pascal/article/details/81478582 FFT前言快速傅里叶变换 (fast Fourier transform),即利 ...
- Git--rebase合并提交
参考 https://blog.csdn.net/hj7jay/article/details/78809547 https://blog.csdn.net/yangcs2009/article/de ...
- mysql 去除重复 Select中DISTINCT关键字的用法(查询两列,只去掉重复的一列)
在使用mysql时,有时需要查询出某个字段不重复的记录,虽然mysql提供 有distinct这个关键字来过滤掉多余的重复记录只保留一条,但往往只用它来返回不重复记录的条数,而不是用它来返回不重记录的 ...
- 吴裕雄--天生自然MySQL学习笔记:MySQL 正则表达式
下表中的正则模式可应用于 REGEXP 操作符中. 实例 查找name字段中以'st'为开头的所有数据: mysql> SELECT name FROM person_tbl WHERE nam ...
- E - Tokitsukaze and Duel CodeForces - 1190C (博弈 + 窗体移动)
"Duel!" Betting on the lovely princess Claris, the duel between Tokitsukaze and Quailty ha ...
- 移动端— position: fixed;固定定位解决方案
这里有个关键的东西叫做viewport,你经常在页面的头部里可以见到它: <meta name="viewport" content="width=device-w ...
- vim 马哥
VIM编辑器 编辑模式 默认 输入模式 i 末行模式 : vim +# file #打开文件后直接跳到第#行 vim + file 直接跳到尾行 vim +/关键字 跳转到 ...
- 京东云数据库RDS SQL Server高可用概述
数据库的高可用是指在硬件.软件故障发生时,可以将业务从发生故障的数据库节点迁移至备用节点.本文主要讲述SQL Server高可用方案,以及京东云RDS数据库的高可用实现. 一.高可用解决方案总览 1. ...
- Java线程——线程之间的几点重要说明
在Java中,可以通过配合调用Object对象的wait()方法和notify()方法或notifyAll()方法来实现线程间的通信.在线程中调用wait()方法,将阻塞等待其他线程的通知(其他线程调 ...
- 吴裕雄--天生自然 JAVA开发学习:Scanner 类
import java.util.Scanner; public class ScannerDemo { public static void main(String[] args) { Scanne ...
