38. docker cloud 简介及 关联 git hub

1.概念

　　提供 容器的管理， 编排， 部署 的托管服务

2.功能

　　image 管理

　　创建 stack

　　创建服务 service

　　添加 节点 作为 docker host

　　自动关联云服务商 AWS  Azure

3. 运行模式

　　standard 模式: 一个 node 就是一个 docker host

　　swarm 模式: 多个 node 组成 swarm cluster

4. 编写一个简单的 Dockerfile

　　FROM

4. 推送 Dockerfile 代码到github

　　https://www.cnblogs.com/arxive/p/6010781.html

　　https://www.cnblogs.com/wmr95/p/7852832.html

4. 自动 build docker image

　　关联 github 账户

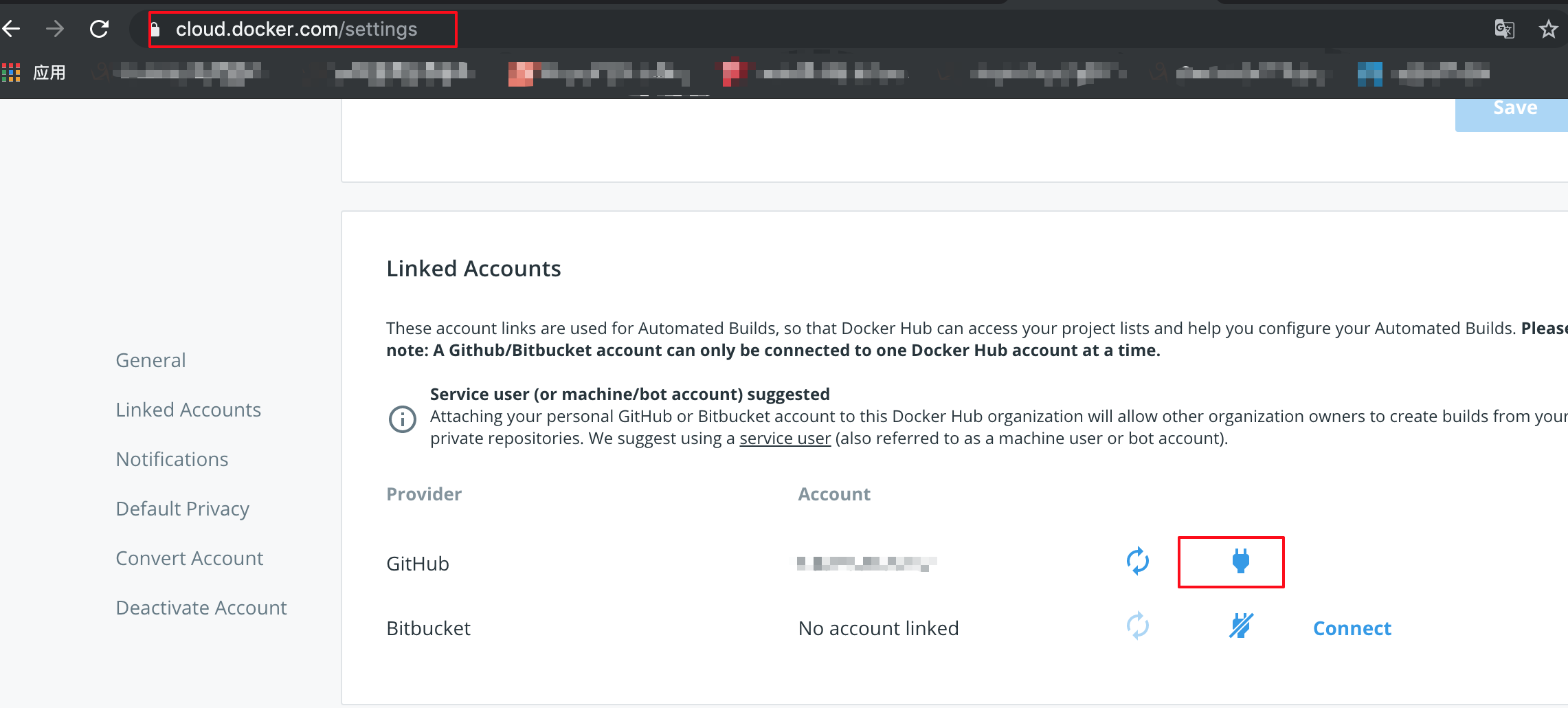
　　　　创建 organization

　　创建 docker repository

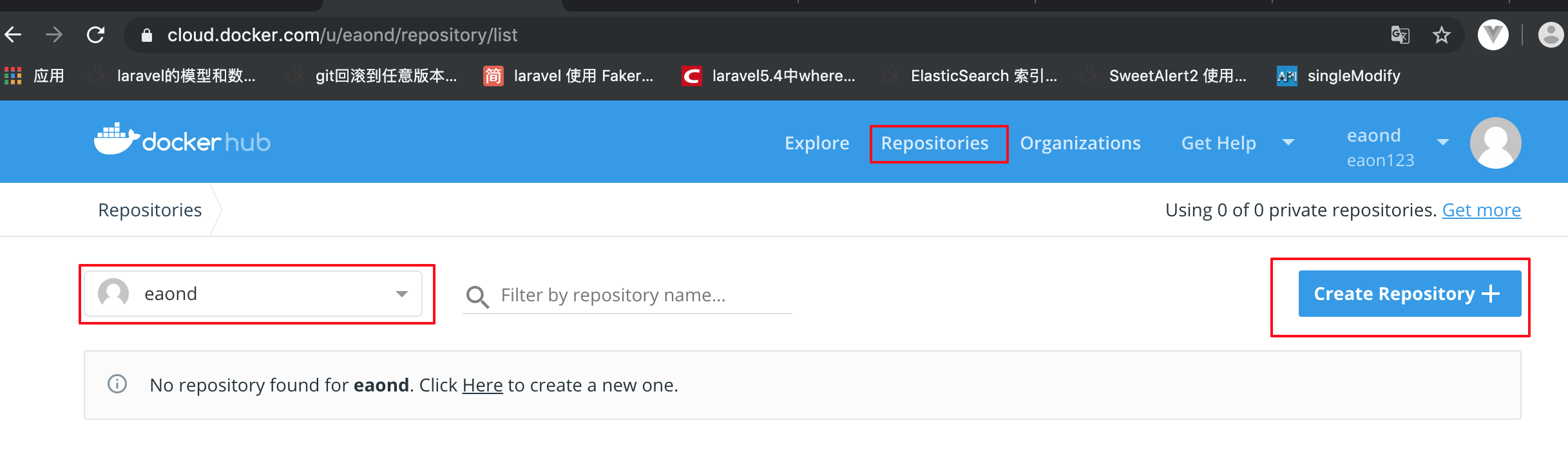
　　填写细节

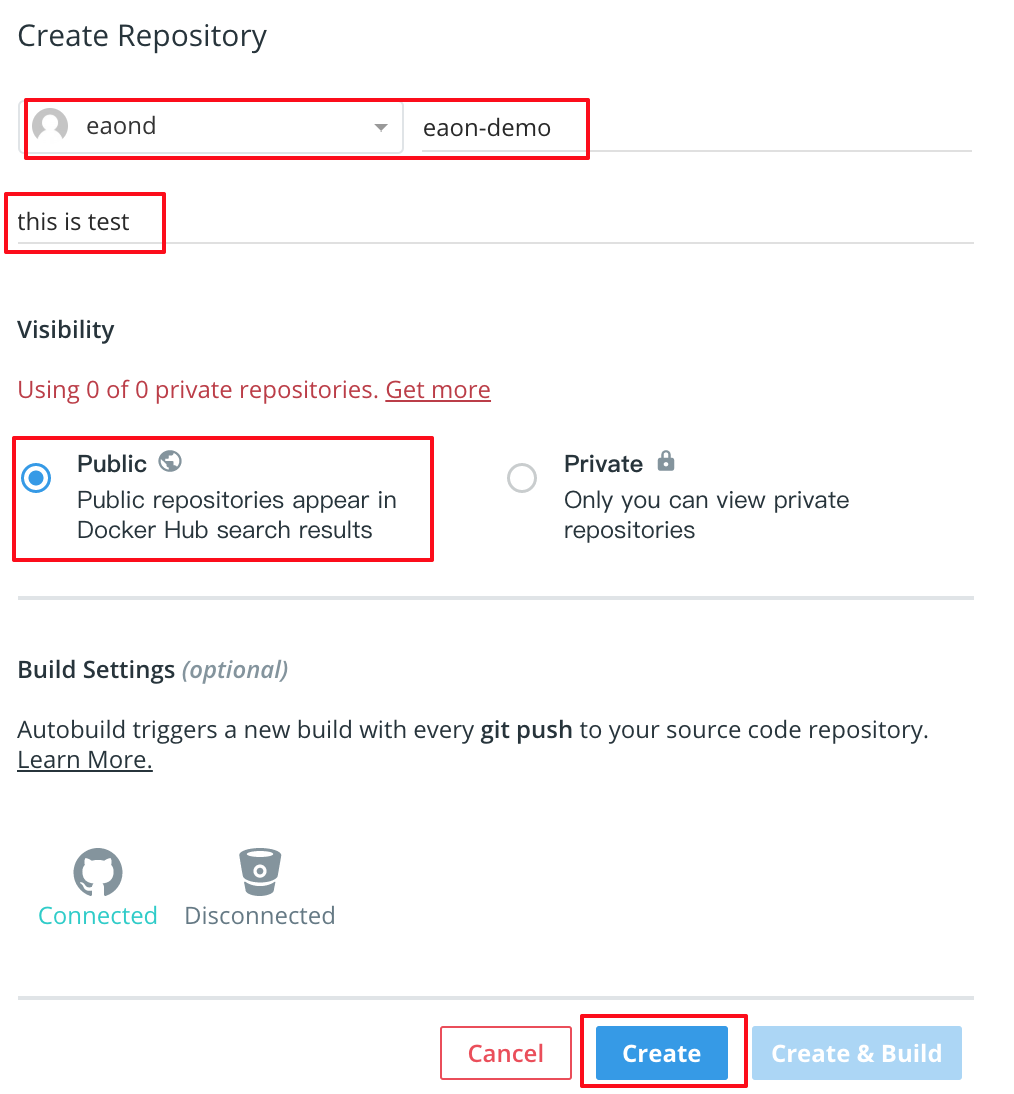
　　点击 进入 生成的 Repositories 选择 builds

　　

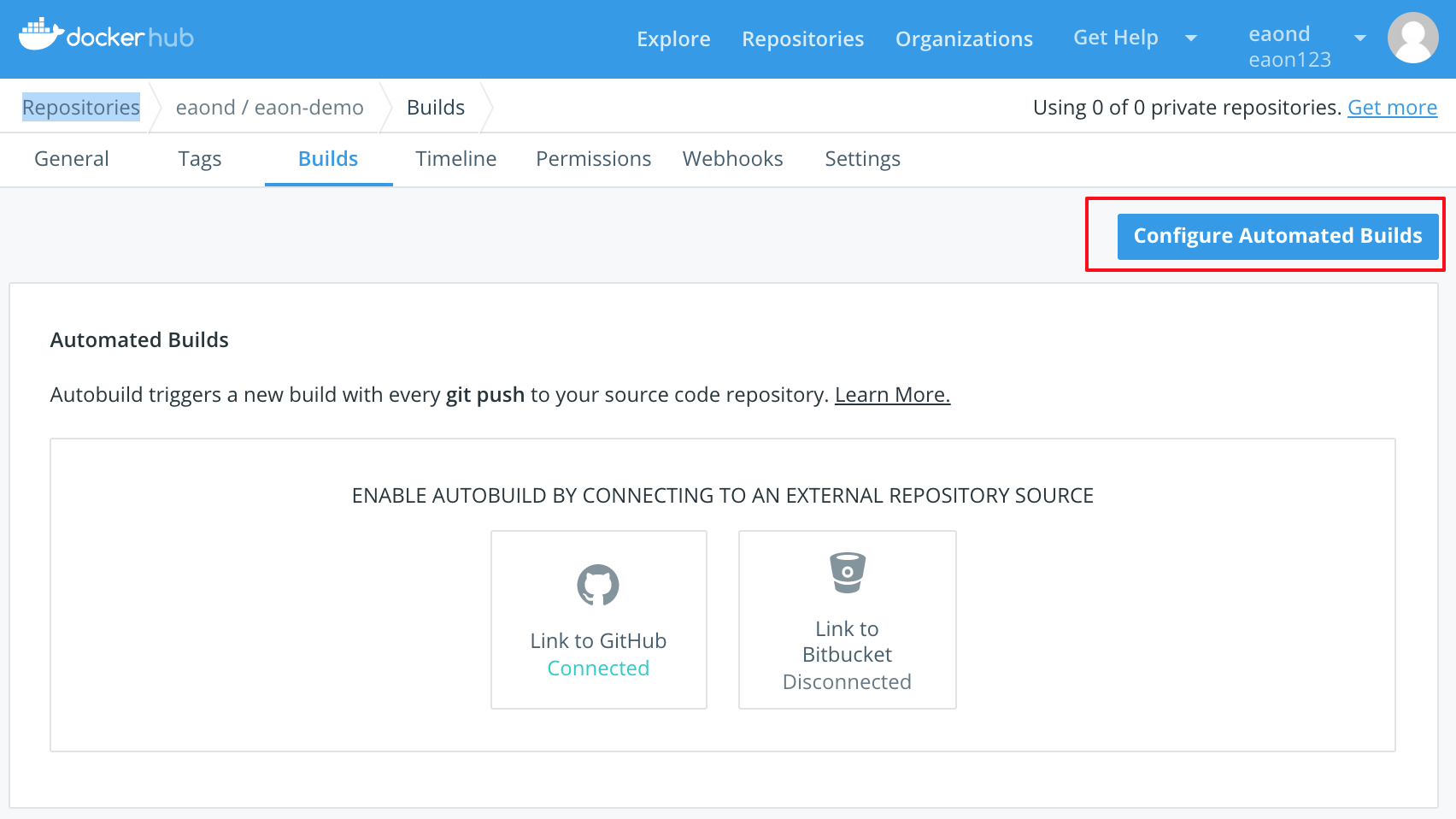
　　选择 关联的 github 的账号 和 仓库  并修改一些