JavaScript图形实例：圆内螺线

数学中有各式各样富含诗意的曲线，螺旋线就是其中比较特别的一类。螺旋线这个名词来源于希腊文，它的原意是“旋卷”或“缠卷”。例如，平面螺旋线便是以一个固定点开始向外逐圈旋绕而形成的曲线。

阿基米德螺线和黄金螺旋线就是典型的螺旋线。下面我们探讨一种典型的螺旋线：圆内螺线。

1．圆内螺线的形成方式

在固定的大圆中内切一个运动的小圆，在小圆滚动的过程中，其上一个定点P所形成的轨迹，即为圆内螺线。点P会随着两圆半径比值的不同而出现不同轨迹。例如，当小圆半径等于大圆的四分之一时，形成的轨迹则是星形线，如图1所示。参见百度百科的词条“圆内螺线”（https://baike.so.com/doc/388206-411038.html）。

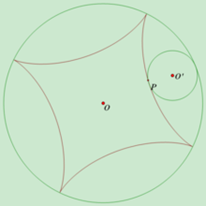
图1 圆内螺线的形成示意图

圆内螺线的笛卡尔坐标参数方程为：

x=cosθ+[cos(nθ)]/n

y=sinθ-[sin(nθ)]/n （0≤θ≤2π， n为大圆半径与小圆半径的比值）

编写如下的HTML代码。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.strokeStyle="red";

context.lineWidth=2;

context.save();

context.translate(150,150);

var R=80; // R+r 为大圆半径

var r=20; // 小圆半径

context.beginPath();

context.arc(0,0,R+r,0,Math.PI*2,true);

context.closePath();

context.stroke();

context.beginPath();

context.arc(0,0,R-r,0,Math.PI*2,true);

context.closePath();

context.stroke();

context.beginPath();

for (theta=0;theta<2*Math.PI;theta+=Math.PI/100)

{

n=R/r;

var x = R*(Math.cos(theta)+Math.cos(n*theta)/n);

var y = R*(Math.sin(theta)-Math.sin(n*theta)/n);

if (theta==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

context.closePath();

context.stroke();

context.restore();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在画布中绘制出圆内螺线图案1，如图2所示。

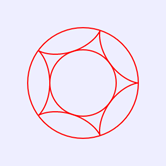
图2 圆内螺线图案1（R=5r）

将大圆半径与小圆半径的比值修改为9，即修改语句“var r=20;”为“var r=10”，则在画布中绘制出如图3所示的圆内螺线图案2。

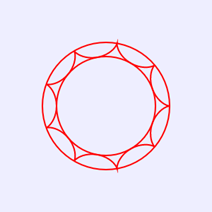
图3 圆内螺线图案2（R=9r）

2．带结环的圆内螺线

我们修改圆内螺线的参数方程，使得螺线在交接处出现结环。修改的参数方程为：

n=(R+r)/r;

x = (R+r)*cos(θ)+(r+o)*cos(n*θ)

y = (R+r)*sin(θ)-(r+o)* sin (n*θ) （0≤θ≤2π）

编写的HTML文件内容如下。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.strokeStyle="red";

context.lineWidth=2;

context.save();

context.translate(150,150);

var R=60; // R+r 为大圆半径

var r=15; // 小圆半径

var o=15;

context.beginPath();

context.arc(0,0,R+2*r+o,0,Math.PI*2,true);

context.closePath();

context.stroke();

context.beginPath();

context.arc(0,0,R-o,0,Math.PI*2,true);

context.closePath();

context.stroke();

context.beginPath();

for (theta=0;theta<2*Math.PI;theta+=Math.PI/100)

{

n=(R+r)/r;

var x = (R+r)*Math.cos(theta)+(r+o)*Math.cos(n*theta);

var y = (R+r)*Math.sin(theta)-(r+o)*Math.sin(n*theta);

if (theta==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

context.stroke();

context.restore();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在画布中绘制出带结环的圆内螺线图案，如图4所示。

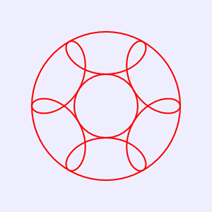
图4 带结环的圆内螺线图案

上面绘制图4的代码不是很完善，例如，我们修改语句“var r=15;”为“var r=24;”，其他语句保持不变，则在画布中绘制出如图5所示图案。这个图案显然不是一条封闭曲线，也就是图案未绘制完整。修改循环控制语句，使得θ范围为[0,3π]，则在画布中绘制出如图6所示图案，这条曲线仍未封闭；当修改循环控制语句，使得θ范围为[0,4π]，才在画布中绘制出如图7所示的封闭曲线图案。

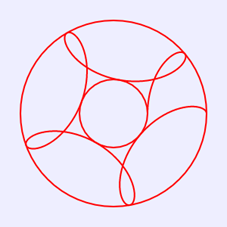
图5 0≤θ≤2π绘制的图案

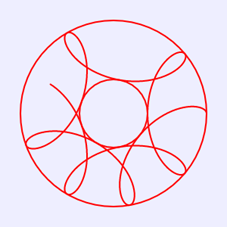
图6 0≤θ≤3π绘制的图案

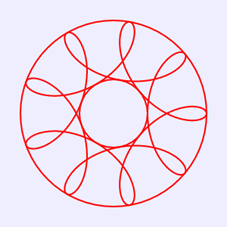
图7 0≤θ≤4π绘制的图案

如何修改程序，使得图案绘制时，无需事先确定θ的取值范围，当曲线闭合时，自动结束绘制呢？

取θ=0时的坐标（x0,y0）为起始点，之后按给定的参数方程依次计算坐标（x,y）并绘图，当计算的坐标点（x,y）与（x0,y0）重合时，结束图形绘制。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.strokeStyle="red";

context.lineWidth=2;

context.save();

context.translate(150,150);

var R=60; // R+r 为大圆半径

var r=24; // 小圆半径

var o=15;

context.beginPath();

context.arc(0,0,R+2*r+o,0,Math.PI*2,true);

context.closePath();

context.stroke();

context.beginPath();

context.arc(0,0,R-o,0,Math.PI*2,true);

context.closePath();

context.stroke();

var x1 = R+2*r+o; // theta=0 时的值

var y1 = 0;

var i = 1;

context.beginPath();

context.moveTo(x1,y1);

do {

if (i>20000) break; // θ最大可达200π

theta=i*Math.PI/100;

n=(R+r)/r;

var x2 = (R+r)*Math.cos(theta)+(r+o)*Math.cos(n*theta);

var y2 = (R+r)*Math.sin(theta)-(r+o)*Math.sin(n*theta);

context.lineTo(x2,y2);

i++;

} while (x2 != x1 && y2 != y1);

context.stroke();

context.restore();

}

</script>

</head>

</body>

</html>

3．另类圆内螺线

修改参数方程为：

n=(R+r)/r;

x = (R+r)*cos(θ)-(r+o)*cos(n*θ)

y = (R+r)*sin(θ)-(r+o)* sin (n*θ) （0≤θ≤kπ，R、r、o取适当值）

编写如下的HTML代码。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.strokeStyle="red";

context.lineWidth=2;

context.save();

context.translate(150,150);

var R=180;

var r=-96;

var o=60;

var x0 = R-o; // theta=0 时的值

var y0 = 0;

var i = 1;

context.beginPath();

context.moveTo(x0,y0);

do {

if (i>20000) break; // θ最大可达200π

theta=i*Math.PI/100;

n=(R+r)/r;

var x = (R+r)*Math.cos(theta)-(r+o)*Math.cos(n*theta);

var y = (R+r)*Math.sin(theta)-(r+o)*Math.sin(n*theta);

context.lineTo(x,y);

i++;

} while (x != x0 && y != y0);

context.stroke();

context.restore();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在画布中绘制出另类螺旋线图案，如图8所示。

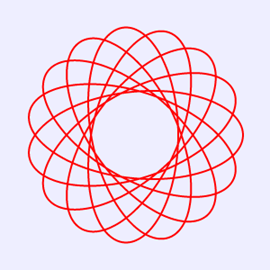
图8 R=180，r=-96，o=60时的螺旋线

修改绘制图8程序中的R、r、o初始值，可以绘制出不同的螺旋曲线。例如，若指定R=160，r=-96，o=40，则在画布中绘制出图9所示的图案；若指定R=160，r=-56，o=40，则在画布中绘制出图10所示的图案；若指定R=66，r=18，o=15，则在画布中绘制出图11所示的图案。

图9 R=160，r=-96，o=40时的螺旋线

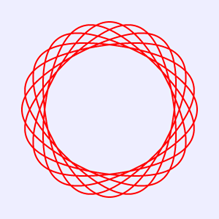
图10 R=160，r=-56，o=40时的螺旋线

图11 R=66，r=18，o=15时的螺旋线