leetcode排列组合相关

目录

• 78/90子集
• 39/40组合总和
• 77组合
• 46/47全排序，同颜色球不相邻的排序方法

78/90子集

输入: [1,2,2]
78输出：
[[], [1], [2], [1 2], [2], [1 2], [2 2], [1 2 2]]
90输出:
[[], [1], [2], [1 2], [2 2], [1 2 2]]

// 递归版简单很多，且与下面的39/40组合总和很相似
public static List<List<Integer>> subsets(int[] nums) {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();
    // subset2用
//      Arrays.sort(nums);
    dfs(res, temp, nums, 0);
    return res;
}

private static void dfs(List<List<Integer>> res, List<Integer> temp, int[] nums, int j) {
    res.add(new ArrayList<>(temp));
    for (int i = j; i < nums.length; i++) {
        // subset2用
//          if (i != j && nums[i] == nums[i-1]) continue;
        temp.add(nums[i]);
        dfs(res, temp, nums, i + 1);
        temp.remove(temp.size() - 1);
    }
}

// 非递归版
// 结果变量
List<List<Integer>> res = new ArrayList<>();
// 方便判断是否出现重复
Arrays.sort(nums);
// 先加上空子集
res.add(new ArrayList<>());
// 用于90
// int last = nums[0], size = 1;
for (int j = 0; j < nums.length; j++) {
    // 用于90，如果出现不同值，就更新size，让下面i从0开始。如果相同，那么size就不需要更新，让i从tempSize - size开始，即去掉了上一轮中已经存在的，从上一轮才更新的数组进行添加。
//      if (last != nums[j]) {
//          last = nums[j];
//          size = res.size();
//      }
    int tempSize = res.size();
    // 遍历，把目前所拥有的所有子集都作为新子集，并在每个新子集中添加新元素
    for (int i = 0; i < tempSize; i++) {
      // 用于90
//    for (int i = tempSize - size; i < tempSize; i++) {
        res.add(new ArrayList<>(res.get(i)));
        res.get(res.size() - 1).add(nums[j]);
    }
}

return res;

39/40组合总和

40（39是无重复元素的数组，所以省去排序。另外允许重复选取元素，所以递归调用函数时index不需要+1）

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

• 所有数字（包括目标数）都是正整数。
• 解集不能包含重复的组合。

思路：

• 排序，防止后面得出重复组合
• 新建midRes和res数组
• 调用递归函数，记录index表示遍历的起始位置（并不是选了多少个candidates）
  • 从index开始遍历candidates
  • 如果i不等于index，且当前遍历与上一个数相同，就continue。（防止得出重复组合）
  • 如果target >= candidates[i]那么可以加入到midRes，然后递归调用函数，在i+1和target-candidates[i]的基础上。然后删除刚刚加入的元素（其实本轮遍历已经结束了），要找新的组合。

if (target == 0) {
    res.add(new ArrayList<>(midRes));
    return;
}

for (int i = index; i < candidates.length; i++) {
    // 由于上面进行了排序，所以相同的数都排在了一起
    // i > index表示i在剩下的组合里已经不是第一个，那如果它和之前的相同，就会重复取值，所以这里continue。当然，如果在无重复元素数组中便不需要这一步和之前的sort
    if (i > index && candidates[i] == candidates[i - 1]) continue;
    if (target >= candidates[i]) { // 所以没有target < 0的情况
        midRes.add(candidates[i]);
        // 由于不能有重复地选取数字，所以i+1，表示上一个已经被取了。
        solve(candidates, i+1, target - candidates[i], midRes, res);
        midRes.remove(midRes.size() - 1);
    }
}

77组合

从n取k个，列出所有不重复组合。

下面代码还有i <= n - k + size +1优化，其思想是，通过观察(5,3)可知，第一层只需遍历到3，第二层才到4，第三层才到5。将这规律扩展开来就能得到这个优化。

// 仿照上面的格式，但index从1开始
dfs(res, temp, n, k, 1);
// dfs
if (temp.size()==k) {
    res.add(new ArrayList<>(temp));
    return;
}
int size = temp.size();
for (int i = j; i <= n - k + size + 1; i++) {
    temp.add(i);
    dfs(res, temp, n, k, i + 1);
    temp.remove(temp.size() - 1);
}

46/47全排序，同颜色球不相邻的排序方法

思路与上面的类似，不同在于这里没有midRes数组，一切操作在原数组中进行。详细解析如下：

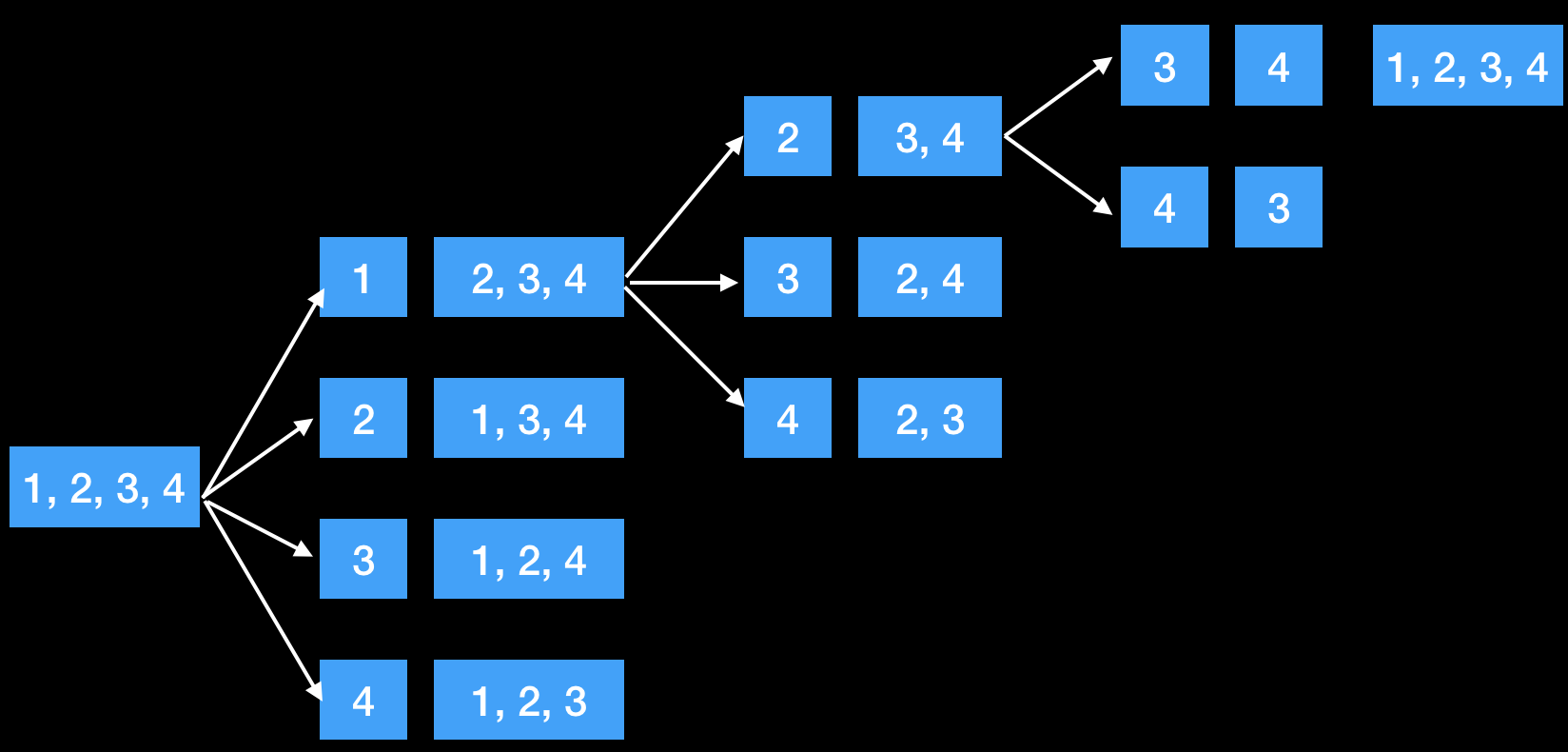
利用递归方法，先固定第一个位置的数，即下面的start，然后后面的数就相当于组成了新数组，所以又固定总体的第二个，即新数组的第一个，所以innerPermute的递归调用中，start+1。可以把innerPermute(nums, start + 1)理解为新数组的全排组合。而如此递归下去后，总会固定到总体的最后一位，即start == nums.length - 1，此时就直接输出当前nums，因为前面的都固定了，就相当于一个排列就已经组成了。另外，在每次求innerPermute(nums, start + 1)前，固定位置的数是可以是当前数字start以及start+1到最后的任意一个数，所以要循环的交换，即下图第一步中，1-1、1-2、1-3、1-4交换，相当于代码中for (int i = start; i < nums.length; i++)和swap(nums, start, i);部分，而交换并求start+1到end这个新数组的全排列后，要再次交换回来。因为在上面循环交换中，1-2交换后，如果不换回来，就变成2-3交换而不是1-3了。这就是代码又多了一个swap(nums, start, i);的原因。

更进一步的permutation就要去重的，即1,1,2只有3个输出（[1,1,2], [1,2,1], [2,1,1]）而不是6个。而去重的方法就是现在交换前，做判断，详细看代码中containsDuplicate的注解。

// 递归函数
if (start == nums.length - 1) { // 如果是“同颜色球不相邻”，不能-1
    List<Integer> tempres = new ArrayList<>();
    for (int num : nums) {
        tempres.add(num);
    }
    res.add(tempres);
}

// start表示固定哪一个，固定后就相当于一个新数组，所以i从start开始
for (int i = start; i < nums.length; i++) {
    if (containsDuplicate(nums, start, i)) { // 用于47去重
        if (start == 0 || (nums[i] != nums[start - 1])) { // 用于“同颜色球不相邻”
        	swap(nums, start, i);
        	innerPermute(nums, start + 1);
        	swap(nums, start, i);
        }
    }
}

// containsDuplicate
// 检查新数组一部分，即start到当前要交换的数之间[start, end-1]，将要交换到start位置的数，外层i，本层的end，是否已经在新数组中出现过，出现过就返回false，跳过这个数的交换。遍历完确定没有出现过才交换。比如[1,2,3,1]中，最后的1-1是不需要交换和取全排的，而判断就是(arr[0] == arr[3]) 返回false。再如比如[1,2,3,2]中，最后的1-2也是不需要交换和取全排的，因为之前已经进行了1-2交换，而判断就是(arr[1] == arr[3]) 返回false。
for (int i = start; i < end; i++) {
    if (arr[i] == arr[end]) {
        return false;
    }
}
return true;