浅谈.NET编译时注入（C#-->IL）

原文:浅谈.NET编译时注入（C#-->IL）

.NET是一门多语言平台，这是我们所众所周知的，其实现原理在于因为了MSIL（微软中间语言）的一种代码指令平台。所以.NET语言的编译就分为了两部分，从语言到MSIL的编译（我喜欢称为预编译），和运行时的从MSIL到本地指令，即时编译（ＪＩＴ）。ＪＩＴ编译分为经济编译器和普通编译器，在这里就不多说了，不是本文的重点。本文主要讨论下预编译过程中我们能做的改变编译情况，改变生成的ＩＬ，从编译前后看看微软Ｃ＃３．０一些语法糖，PostSharp的静态注入等等。

１：我们先来看看最简单的var:

Ｃ#:

public void TestVar(){ 
   var i = 0;   Console.WriteLine(i);}

使用Reflector查看生成

ＩＬ：

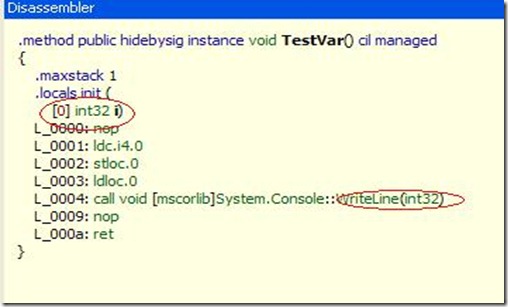
反编译后的Ｃ＃：

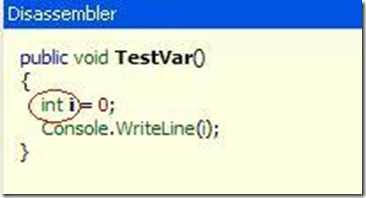
这里ＶＳ在编译的时候将ｖａｒ为我们转变为了ｉｎｔ类型。

２：Action<int>：

Ｃ＃：

public void TestAction(){var i = 1;Func<int,int> f = t => t+1;i=10;f(i);}

反编译后Ｃ＃：

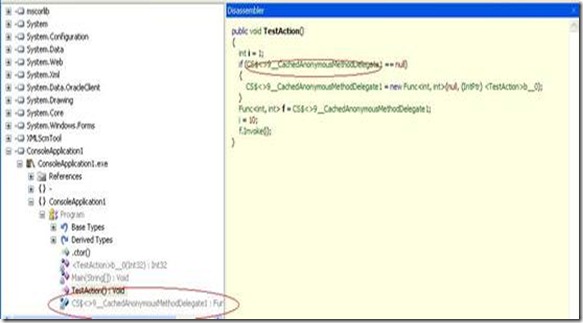
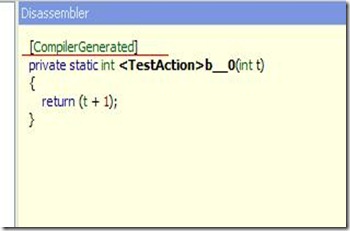
编译器为我们在这里生成了代理方法。

总结：

关于lambda表达式的编译规则：

当一个lambda expression被赋值给一个delegate类型，例如Action<T>或者Func<T, TResult>等，这个lambda expression会被编译器直接编译为
1) 当lambda expression没有使用闭包内的非局部引用也没有使用到this时，编译为一个私有静态方法；
2) 当lambda expression没有使用闭包内的非局部引用，但用到了this时，编译为一个私有成员方法；
3) 当lambda expression中引用到非局部变量，则编译为一个私有的内部类，将引用到的非局部变量提升为内部类的。

３：PostSharp：

PostSharp是结合了 MSBuild Task 和 MSIL Injection 技术，编译时静态注入实现 AOP 编程。在编译时候改变VS的编译行为。更详细的信息，请访问 PostSharp 网站

原ｃ＃：

using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication1{class Program{static void Main(string[] args){new Program().TestPostSharp();}[ErrorHandler()]public void TestPostSharp(){throw new Exception("I will throw a exception!");}}[Serializable]public class ErrorHandlerAttribute : PostSharp.Laos.OnMethodBoundaryAspect{public override void OnException(PostSharp.Laos.MethodExecutionEventArgs eventArgs){//do some AOP operation!Console.WriteLine(eventArgs.Method+":" +eventArgs.Exception.Message);eventArgs.FlowBehavior = PostSharp.Laos.FlowBehavior.Continue;}}}

反编译后：

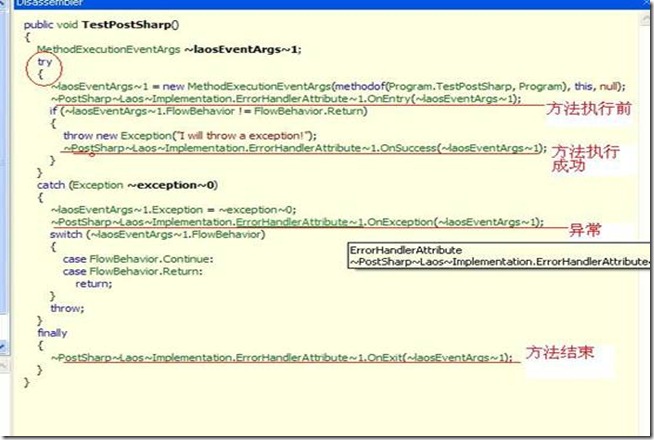
今天就到此为至,只是简单的了解下IL注入实例,在后面会利用MSBuild Task+Mono Cecil 和PostSharp实现一些简单的注入实例.