洛谷P3374 【模板】树状数组 1（CDQ分治）

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3个整数，表示一个操作，具体如下：

操作1： 格式：1 x k 含义：将第x个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1： 复制

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出样例#1： 复制

14
16

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

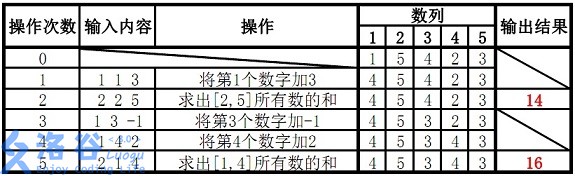
故输出结果14、16

CDQ分治维护二维偏序

第一维用排序搞掉

第二维用CDQ分治

慢的要死。。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<ctime>
 #include<cstdlib>
 using namespace std;
 #define ls T[now].ch[0]
 #define rs T[now].ch[1]
 const int MAXN=*1e6+;
 inline char nc()
 {
     static char buf[MAXN],*p1=buf,*p2=buf;
     return p1==p2&&(p2=(p1=buf)+fread(buf,,MAXN,stdin),p1==p2)?EOF:*p1++;
 }
 inline int read()
 {
     char c=nc();int x=,f=;
     while(c<''||c>''){if(c=='-')f=-;c=nc();}
     while(c>=''&&c<=''){x=x*+c-'',c=nc();}
     return x*f;
 }
 int n,m;
 struct node
 {
     int idx;//第几次询问
     int val;//修改的值
     int type;//操作类型
     bool operator<( const node &a) const {
         return idx==a.idx?type<a.type:idx<a.idx;}
 }Q[MAXN];
 int qidx=;//操作的个数
 int aidx=;//询问的个数
 int ans[MAXN];
 node tmp[MAXN];
 void CDQ(int l,int r)
 {
     if(r-l<=)    return ;
     int mid=(l+r)>>;CDQ(l,mid);CDQ(mid,r);
     int sum=;
     int p=l,q=mid,o=;
     while(p<mid&&q<r)
     {
         if(Q[p]<Q[q])
         {
             if(Q[p].type==) sum+=Q[p].val;
             tmp[o++]=Q[p++];
         }
         else
         {
             if( Q[q].type==)    ans[Q[q].val]-=sum;
             else if(Q[q].type==)    ans[Q[q].val]+=sum;
             tmp[o++]=Q[q++];
         }
     }
     while(p<mid) tmp[o++]=Q[p++];
     while(q<r)
     {
         if( Q[q].type==)    ans[Q[q].val]-=sum;
         else if(Q[q].type==)    ans[Q[q].val]+=sum;
         tmp[o++]=Q[q++];
     }
     for(int i=;i<o;i++) Q[i+l]=tmp[i];
 }
 int main()
 {
     #ifdef WIN32
     freopen("a.in","r",stdin);
     #else
     #endif
     n=read();m=read();
     for(int i=;i<=n;i++)
     {
         Q[qidx].idx=i;
         Q[qidx].type=;
         Q[qidx].val=read();++qidx;
     }
     for(int i=;i<m;i++)
     {
         int type=read();
         Q[qidx].type=type;
         if(type==)    Q[qidx].idx=read(),Q[qidx].val=read();
         else
         {
             int l=read(),r=read();
             Q[qidx].idx=l-;Q[qidx].val=aidx;++qidx;
             Q[qidx].type=;Q[qidx].idx=r;Q[qidx].val=aidx;aidx++;
         }
         ++qidx;
     }
     CDQ(,qidx);
     for(int i=;i<aidx;i++)    printf("%d\n",ans[i]);
     return ;
 }