[CSP-S模拟测试]:组合（欧拉路）

题目传送门（内部题119）

---

输入格式

　　第一行，三个整数$T,M,N$。
　　接下来的$N$行，每行两个整数$u_i,v_i$（$i$从$1$开始编号）。允许$u_i=v_i$，也允许同样的简单词多次出现。

---

输出格式

　　第一行，一个字符串$YES$或$NO$，表示能否将这$N$个简单词组合成一个复杂词。
　　如果能，则第二行输出$N$个整数，第$i$个数$p_i$表示组成复杂词的第$i$个简单词是输入的编号为$|p_i|$的简单词。注意，当$T=1$且使用编号为$|p_i|$的简单词时交换了两个字符的顺序，则输出编号的相反数，否则输出编号。如果有多组解，输出任意一组即可。

---

样例

样例输入1：

1 3 2
2 3
1 3

样例输出1：

YES
2 -1

样例输入2：

2 5 5
2 3
2 5
3 4
1 2
4 2

样例输出2：

YES
4 1 3 5 2

---

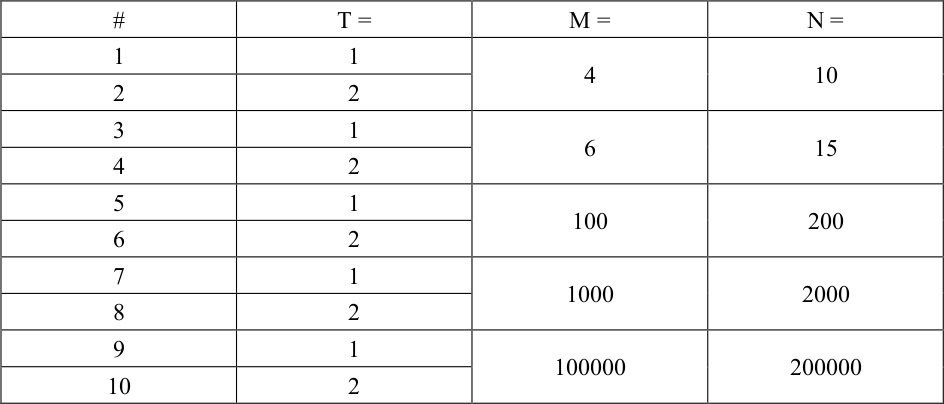
数据范围与提示

样例$1$解释：

如果用$a,b,c$分别表示字符$1,2,3$，则第一个简单词为$bc$，第二个简单词为$ac$，所以可以交换第一个简单词的两个字符，这样就可以组合成$acb$，所以输出$2\ -1$。

数据范围：

---

题解

先来明确一下题意，对于$T=1$的情况，可以交换多个，而不是一个。

转化题意，对于$T=1$的情况，则是找无项图的欧拉路；对于$T=2$的情况，则是有向图。

代码实现上需要注意环的情况，还需要反着输出。

时间复杂度：$\Theta(N+M)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to,w;}e[400002];
int head[200001],cnt=1,tot,top,sum;
int T,M,N;
pair<int,int> a[200001];
int ans[200001],sta[200001],du[200001],in[200001],out[200001];
bool vis[400002],v[200001];
void add(int x,int y,int w)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	e[cnt].w=w;
	head[x]=cnt;
}
void dfs(int x)
{
	vis[x]=1;
	tot++;
	for(int i=head[x];i;i=e[i].nxt)
		if(!vis[e[i].to])dfs(e[i].to);
}
void dfs1(int x,int in)
{
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(vis[i])continue;
		vis[i]=vis[i^1]=1;
		head[x]=i;
		dfs1(e[i].to,i);
		i=head[x];
	}
	ans[++ans[0]]=e[in].w;
}
void dfs2(int x,int in)
{
	if(!v[x]){v[x]=1;tot++;}
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(vis[i])continue;
		head[x]=i;
		vis[i]=1;dfs2(e[i].to,i);
		i=head[x];
	}
	ans[++ans[0]]=e[in].w;
}
void work1()
{
	for(int i=1;i<=N;i++)
	{
		scanf("%d%d",&a[i].first,&a[i].second);
		if(!vis[a[i].first]){vis[a[i].first]=1;sum++;}
		if(!vis[a[i].second]){vis[a[i].second]=1;sum++;}
		add(a[i].first,a[i].second,i);
		add(a[i].second,a[i].first,-i);
		du[a[i].first]++;
		du[a[i].second]++;
	}
	memset(vis,0,sizeof(vis));
	dfs(a[1].first);
	if(sum!=tot){puts("NO");exit(0);}
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=N;i++)
	{
		if((du[a[i].first]&1)&&!vis[a[i].first]){sta[++top]=a[i].first;vis[a[i].first]=1;}
		if((du[a[i].second]&1)&&!vis[a[i].second]){sta[++top]=a[i].second;vis[a[i].second]=1;}
	}
	memset(vis,0,sizeof(vis));
	if(!top)dfs1(a[1].first,0);
	else if(top==2)dfs1(sta[1],0);
	else{puts("NO");exit(0);}
	puts("YES");
	for(int i=N;i;i--)printf("%d ",ans[i]);
}
void work2()
{
	for(int i=1;i<=N;i++)
	{
		scanf("%d%d",&a[i].first,&a[i].second);
		if(!vis[a[i].first]){vis[a[i].first]=1;sum++;}
		if(!vis[a[i].second]){vis[a[i].second]=1;sum++;}
		add(a[i].first,a[i].second,i);
		out[a[i].first]++;
		in[a[i].second]++;
	}
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=N;i++)
	{
		if(in[a[i].first]!=out[a[i].first])
		{
			if(in[a[i].first]!=out[a[i].first]+1&&in[a[i].first]!=out[a[i].first]-1){puts("NO");exit(0);}
			if(!vis[a[i].first]){sta[++top]=a[i].first;vis[a[i].first]=1;}
		}
		if(in[a[i].second]!=out[a[i].second])
		{
			if(in[a[i].second]!=out[a[i].second]+1&&in[a[i].second]!=out[a[i].second]-1){puts("NO");exit(0);}
			if(!vis[a[i].second]){sta[++top]=a[i].second;vis[a[i].second]=1;}
		}
	}
	memset(vis,0,sizeof(vis));
	if(!top)dfs2(a[1].first,0);
	else if(top==2)
	{
		if(in[sta[1]]==out[sta[1]]-1)dfs2(sta[1],0);
		if(in[sta[2]]==out[sta[2]]-1)dfs2(sta[2],0);
		if(in[sta[1]]==out[sta[1]]-1&&in[sta[2]]==out[sta[2]]-1){puts("NO");exit(0);}
		if(in[sta[1]]==out[sta[1]]+1&&in[sta[2]]==out[sta[2]]+1){puts("NO");exit(0);}
	}
	else{puts("NO");exit(0);}
	if(tot!=sum){puts("NO");exit(0);}
	puts("YES");
	for(int i=N;i;i--)printf("%d ",ans[i]);
}
int main()
{
	scanf("%d%d%d",&T,&M,&N);
	if(T==1)work1();
	else work2();
	return 0;
}

---

rp++