图论之点双&边双

说人话：

边双联通：

a到b的路径上无必经边

点双联通：

a到b的路径上除了a,b没有必经点

tarjan求点双联通：

代码（补图）

割点：

桥：

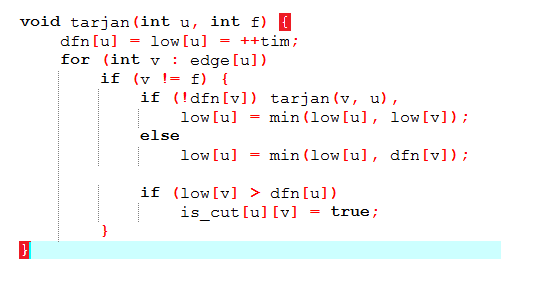
求点双：强制dfs时不越过割点，即可求出一个块

求边双：dfs时不越过桥

不是割点：减少2n-1

是割点：减少sigmai的大小*其他所有子树的大小

tarjan求桥，然后缩点，会形成一棵树。把树的所有叶子连起来用的边数就是答案

判断：

当且仅当无向图上不含奇环的时候就是二分图

增广路特点：非匹配边比匹配边多一条

寻找增广路：dfs

咕咕咕~

网络流：

最小割最大流定理：网络流的最大流就是整个图的最小割

dinic:类似匈牙利算法的思路，不断寻找当前最大流能加1的方案

直到不能再加

先dfs一遍，确定每个点到源点s的距离，

同时不断加边，维护当前流量

毒瘤操作：减少某条边的流量

所以就减反向边，边权为0，表示从终点到起点可扩充流量

二分图最大匹配怎么用网络流搞？

在左边建一个超级源点s，在右边建一个超级汇点t

s向每个左边的点建一个流量为1的边，右边的点向t建流量为1的边

二分图中间的点不停的寻找能加流量的路，能加就加，知道不能加

总之最大流就是最大匹配

二分图建图小技巧：

如果有x轴,y轴，且有一个坐标(x0,y0)

则就由x0向y0建一条边

国际象棋棋盘：黑白染色（黑的向白的建边）

就是最小覆盖qwq

因为消灭一行x0就是把x0那个点的所有连边都覆盖掉

消灭一列同理

所以打一次抢就相当于覆盖一撮边

最小顶点覆盖=最大匹配数

特别的，一个点也是一个路径

玄学转化二分图：

|v|是顶点个数

为什么上面说的是对的？

假设我们现在覆盖到了u,再从u选择一条出边，到了v,v就不用再来一条路径搞覆盖了。所以每多选一条边，答案就减1.

//图

但是每个点只能选出一条出边，一条入边。对于每个点，我们把它拆成两个，一个出点，一个入点。

所以就这么玄学的转化成了二分图

我们选的边在二分图上就是一个匹配

窝盟每选一条边，那么就有一个点不用再来一条路径进行覆盖了，也就是答案会在原来的基础上-1.所以我们要选出尽可能多的边来覆盖尽可能多的点，设覆盖的点最多为k,则答案就是n-k。

按照上述的转化方式，就是求转化后的二分图最大匹配 

建大约n²条边然后最小路径覆盖？？？

还真是啊.....

然后就搞完了

匈牙利算法说人话：

找到一个点v：v是非匹配点----->把这条边设为匹配边，再找非匹配边；

v是匹配点-------->走完这条匹配边，到了边的终点，然后再找非匹配边

今天莫得糖果，所以就分白砂糖好了，一人一堆慢慢数有几颗

裸的查分约束，少的向多的建边权为1的边

大于等于:边权为0，小的向大的建边

小于等于：边权为0，还是小的向大的建边

玄学建边方向判断：

现在有这样的一条边

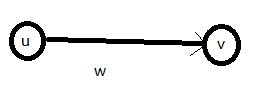
跑最短路

dis[v]<=dis[u]+w

跑最长路：

dis[v]>=dis[u]+w

根据选择跑的路推一推就知道谁想谁建边辣

出现等于：连大于等于，小于等于

最短or最长？

迷惑行为大赏

跑最长路

why?因为要考虑所有的约束条件啊

看一张丑陋的图就知道为什么了

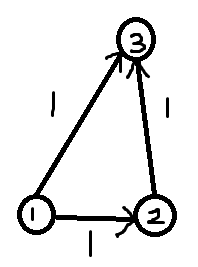
显然dis[3]是2不是1

出现正环就药丸

超级源点的d为0

ysq:论是账本伪造还是刁姹算错？？？

[l,r]的加起来=k,则xr-xl=k

我们可以处理出前缀和数组s[i],表示前i个数的和

这样就会有s[r]-s[l-1]=k的形式的约束条件

我们拆成s[r]-s[l-1]>=k和s[r]-s[l-1]<=k这两个

边权是k或-k

当然了这个前缀和数组也是充满了毒瘤

需要我们跑最短路维护前缀和

然后dfs找有没有负环

当然还有更为玄学的直接dfs

点的权值就是s[i]的值

弄好了s[i]之后直接看是否合法即可

爆......爆搜？！

仍旧是按照二分图建图的duliu建法，每次就相当于在某一个点的所有出边的边权+1或-1,然后限制就是(x,y)这条边的边权是c

于是我们考虑爆搜（当出现冲突的时候说明无解）