SVM的推导和理解

主要记录了SVM思想的理解,关键环节的推导过程,主要是作为准备面试的需要.

1.准备知识-点到直线距离

点\(x_0\)到超平面(直线)\(w^Tx+b=0\)的距离,可通过如下公式计算:
\[ d = \frac{w^Tx_0+b}{||w||}\]
因为公式分子部分没有带绝对值,因此计算得到的d有正负之分.因为超\(w^Tx+b=0\)将空间分为两部分(以2维为例,直线\(w_1x+w_2y+b=0\),将二维空间划分为上下两部分),其中一部分d大于0,另一部分d小于0.

上面距离公式的简单推导过程如下:

超平面\(w^Tx+b=0\)的一个法向量为\(w\):
因为对于超平面上任意不同的两点\(x_0,x_1\),他们所构成的向量\((x_1-x_0)\),与\(w\)的内积为:
\[\begin{align}
w^T(x_1-x_0) &= w^Tx_1-w^Tx_0\\
&= -b-(-b)\\
&= 0
\end{align}\]
即,\(w\)与超平面上任意向量(直线)正交,即\(w\)为超平面的法向量,\(\frac{w}{||w||}\)为超平面的单位法向量.
点\(x_0\)到超平面\(w^Tx+b=0\)的距离等于,平面上任意一点\(x_1\)与点\(x_0\)构成的向量在单位法向量上的投影,即:
\[\begin{align}
d &= \frac{w^T(x_0-x_1)}{||w||}\\
&= \frac{w^Tx_0-w^Tx_1}{||w||}\\
&= \frac{w^Tx_0-(-b)}{||w||}\\
&= \frac{w^Tx_0+b}{||w||}\\
\end{align}\]

2. 支持向量机的数学表示

SVM的图示如下,主要思想是寻找使得margin最大的超平面,该超平面为两条平行的边界超平面的中心.

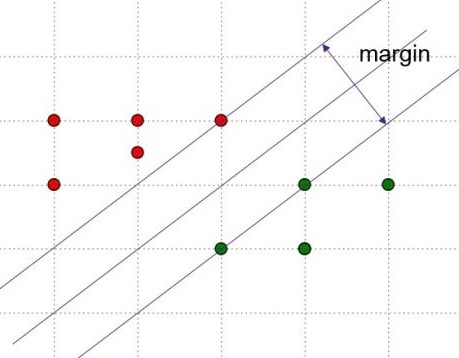
假设分类的超平面为\(w^Tx+b=0\),两个平行的边界超平面分别为
\[\begin{cases}
w^Tx+b=l\\
w^Tx+b=-l\\
\end{cases}\]
因为\(\frac{w}{l}^Tx+\frac{b}{l}=0\)与\(w^Tx+b=0\)是同一个超平面,所以等式两边同除以\(l\),并进行变量替换后,边界超平面可以定义为如下形式:
\[\begin{cases}
w^Tx+b=1\\
w^Tx+b=-1\\
\end{cases}\]
样本被两个边界超平面分隔开,假设对于标签\(y_i=1\)的样本,\(w^Tx_i+b\ge 1\).则对于标签\(y_i=-1\)的样本,\(w^Tx_i+b\le -1\).两种情况可以统一为下式:\[y_i(w^Tx_i+b)\ge 1\]
边界平面\(w^Tx+b=1\)上任意一点到分类超平面\(w^Tx+b=0\)的距离为:\(d =\frac{1}{||w||}\),margin为其二倍,等于\(\frac{2}{||w||}\).则SVM求解的过程就是求解\(max_w\frac{2}{||w||}\)的过程,该过程等同于\(min_w\frac{1}{2}||w||^2\).
至此,我们将SVM转换为带有条件约束的最优化问题:
\[\begin{cases}
min_w\frac{1}{2}||w||^2\\
y_i(w^Tx_i+b)\ge 1\\
\end{cases}\]

3.SVM的求解思路

对于上面带有约束条件的凸优化问题,构造如下拉格朗日函数:
\[L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum_{i}\alpha_i(1-y_i(w^Tx_i+b))\]
则原带有约束条件的问题可以等价为\(min_{w,b}max_{\alpha}L(w,b,\alpha)\),将min和max互换顺序,得到原问题的对偶问题,\(max_{\alpha}min_{w,b}L(w,b,\alpha)\),令\(\theta(\alpha) = min_{w,b}L(w,b,\alpha)\),则对偶问题可以表示为\(max_{\alpha}\theta(\alpha)\)

因为SVM原问题为凸优化问题,在slater条件满足是,原问题与对偶问题等价,可以通过求解对偶问题得到原问题的最优解(因为KKT条件为强对偶的必要条件,则此时KKT条件必然也是满足的).

求解\(\theta(\alpha)\),令\(L(w,b,\alpha)\)对\(w,b\)的偏导数为零:
\[\begin{cases}
\frac{\partial L(w,b,\alpha)}{\partial w} = 0\\
\frac{\partial L(w,b,\alpha)}{\partial b} = 0\\
\end{cases}\]
可以得到(本处省略了具体的求导过程):
\[\begin{cases}
w = \sum_{i}\alpha_iy_ix_i\\
\sum_{i}\alpha_iy_i = 0\\
\end{cases}\]
将\(w,b\)带入\(L(w,b,\alpha)\)可得\(\theta(\alpha)\)如下(省略了具体的带入求解过程):
\[\theta(\alpha) = \sum_{i}\alpha_i - \frac{1}{2}\sum_{i,j}\alpha_i\alpha_jy_iy_jx_i^Tx_j\]
对偶问题最终可以如下表示:
\[\begin{cases}
max_\alpha \sum_{i}\alpha_i - \frac{1}{2}\sum_{i,j}\alpha_i\alpha_jy_iy_jx_i^Tx_j\\
\alpha_i \ge 0\\
\sum_{i}\alpha_iy_i = 0\\
\end{cases}\]
\(\alpha_i \ge 0\)是拉格朗日因子本身需要满足的条件,\(\sum_{i}\alpha_iy_i = 0\)是\(L(w,b,\alpha)\)对\(b\)偏导为0的约束.

求解上式(利用SMO算法,比较复杂本处省略),可以得到最优的一组\(\alpha_i^*\).然后利用\(w^* = \sum_{i}\alpha_i^*y_ix_i\)求解得到最优的\(w^*\).假设\(x_+,x_-\),分别为两个边界超平面上的点,则\(w^*x_++b^*=1\),\(w^*x_-+b^* = -1\),两式相加可得:
\[b^* = -\frac{w^*x_++w^*x_-}{2}\]
根据KKT条件,\(\alpha^*_i(y_i(w^*x_i+b)-1)=0\),则若\(\alpha^*_i>0\),则\(y_i(w^*x_i+b)-1=0\),即\(x_i\)在边界分类超平面上.则求解b过程中的\(x_+,x_-\)可以在\(\alpha^*_i>0\)的\(x_i\)中寻找.

4.soft margin的理解

对于线性不可分的样本(有噪声干扰),可以适当放松边界超平面,以得到更好的鲁棒性能.soft margin形式下的SVM定义如下:
\[\begin{cases}
min_{w,b,\xi}\frac{1}{2}||w||^2+C\sum_{i}\xi_i\\
y_i(w^Tx_i+b)\ge 1-\xi_i\\
\xi_i\ge0
\end{cases}\]
其中,C为\(\xi_i\)的惩罚因子,C越大,对\(\xi\)的惩罚越大,\(\xi\)的可能取值越小,soft margin效果越弱,鲁棒性能越差,反之亦然.

5.核技巧的理解

核函数能够带来非线性能力,通过将特征映射到高维空间,使得在低维空间中非线性可分的样本在高位空间中线性可分.
SVM对样本分类的判别方法为:\(w^Tx+b\ge0\),则\(y=1\),否则\(y=0\)
在本文前面分析过程中可到:\(w^* = \sum_{i}\alpha_i^*y_ix_i\),带入判别式可得:\(\sum_{i}\alpha_i^*y_ix_i^Tx+b\ge0\),即\(\sum_{i}\alpha_i^*y_i<x_i,x>+b\ge0\).
将上面特征向量的内积换成核函数的内积,即可以得到核函数下SVM的判别表达式:\(\sum_{i}\alpha_i^*y_i<K(x_i),K(x)>+b\ge0\),实际上,在使用核函数时我们并不需要先将特征映射到高维,再在高维进行内积运算,我们往往直接在低维计算出高位内积的结果,这样并没有因维度增加而显著增加计算量.即上式一般改写为:\(\sum_{i}\alpha_i^*y_iK(x_i,x)+b\ge0\).