【6.12校内test】T3 城市交通费

要不我先去写T2吧（逃

先把题目搞上来：

【问题描述】 有 n 个城市，编号 1~n。其中 i 号城市的繁华度为 pi。省内有 m 条可以双向同行的高速 公路，编号 1~m。编号为 j 的高速公路连接编号为 aj 和 bj 两个城市，经过高速公路的费用 是 wj。若从城市 x 出发到某城市 y，除了需要缴纳高速公路费用，还要缴纳“城市建设费” （为从 x 城市到 y 城市所经过的所有城市中繁华度的最大值，包括 x 和 y 在内）。

现提出 q 个询问，每个询问给出一组 x 和 y，你需要回答从 x 出发到 y 城市，所需要的 最低交通费（高速公路费+城市建设费）是多少。

【输入】

第一行三个整数 n,m,q。 第二行 n 个整数，表示 p1~pn。

接下来 m 行中，每行 3 个正整数，第 j 行包含 Aj，Bj，Wj。

随后 Q 行每组两个正整数 x，y 表示一组询问。

【输出】

共 Q 行，为对 Q 个问题的回答：x 城市到 y 城市的最小交通费用。

【样例输入】

5 7 2

2 5 3 3 4

1 2 3

1 3 2

2 5 3

5 3 1

5 4 1

2 4 3

3 4 4

1 4

2 3

【样例输出】

8 9

【数据范围及约定】

n≤250，m≤20000，Q≤10000，Pi≤10000，Wj≤2000，保证任意两个城市可以互相到达。

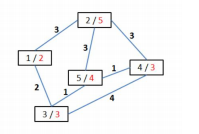
【样例说明】 图中，代表城市的格子中第一个数字是城市编号，第二个红色数字是该城市的繁华度。

（1）从城市 1 到城市 4 的最小交通费用路线是：1 3 5 4；公路费是 2+1+1=4；城市建设费是 max{2,3,4,3}=4；总交通费用 4+4=8。

（2）从城市 2 到城市 3 的最小交通费用路线是：2 5 3；公路费是 3+1=4；城市建设费是 max{5,4,3}=5；总交通费用 4+5=9。

---

(跑回来补锅：

SOLUTION：

1. 首先当然是存图啦，这里用邻接矩阵存图就好了。但是你以为这么容易的吗，你永远想想不到毒瘤出题人是怎么想的，这套题的数据点居然两个城市之间有超过一条的路径？？？慌得一批，这数据也是毒瘤的没谁了；
2. 接下来是一些跑floyd的初始化：因为要加繁华度，因此我们要开两个二维数组来分别记录只最短路和加了繁华度的最短路；对于只记录最短路的二维数组a[i][j]，用memset初始化为一个很大的数，在楼上存图时记得更新某两点间有一条路径（顺序写反了但是不想改），接下来顺带讲一下memset的赋值是怎么赋的：
   • memset按位赋值：一位等于8字节（一个int型是4位），（一字节可以看做是二进制中的一位），对于memset，无论你这个数是什么，它都会把每一位都变成第一位的数，如果我们用memset赋值1的话，最后结果就是这个数：

（一个蓝框为1位）

而本题中memset（a，63,sizeof（a））；就是把a数组的初始值赋成了以下这个数：

好了继续讲初始化：初始化a[i][i]=0（自己到自己显然是0），用一个数组t[i]来记录下标，讲t数组按繁华度从小到大排序（讲真的这个排序我是第一次见/果真还是我太蒟了吗qwq）

这样我们来看一看样例排序后：也就是现在t[1]---t[n]分别对应着繁华度最低的城市的编号到繁华度最高的城市的编号；

预处理f[i][j]=a[i][j]+max（p[i],p[j]）；这样如果两城市之间本来就有路联通的话，那么可以先被更新掉，如果不连通，可以近似的看为INF；

3.最核心的floyd部分，也是大家讨论了好久的部分：

1. 1. floyd实际上是一个DP（floyd：哈哈想不到吧qwq）
   2. floyd其实是一个三维DP
   3. floyd其实就跟01背包一样把k这一维降掉了，因此k要放在最外层枚举；
   4. 对于没有降维的三维floyd dis_{k,i,j来讲，表示的是从i=>j只可能经过1——k这些点的最短路径；}
   5. 对于这个题来讲：f[k][i][j]表示的就是从i=>j只可能经过1——k这前k个繁华福低的城市，因为这里枚举的k其实枚举的是第k的最不繁华城市，所以此时k城市一定是1——k中繁华度最高的，因此对于f[i][j]来说，此时要加的繁华度就是i城市，j城市和k城市中最大的一个；

4.最后就是输入询问然后直接输出f[x][y]就好啦

（撒花✿✿ヽ(°▽°)ノ✿）

#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
using namespace std;
int n,m,q,p[],aj,bj,wj,x,y,f[][],a[][],top,t[];
int cmp(int x,int y)
{
    return p[x]<p[y];
}
int main()
{
    memset(a,,sizeof(a));
    top=;
    scanf("%d%d%d",&n,&m,&q);
    for(int i=;i<=n;i++)
        scanf("%d",&p[i]);
    for(int i=;i<=m;i++)
    {
        scanf("%d%d%d",&aj,&bj,&wj);
        a[aj][bj]=min(a[aj][bj],wj);
        a[bj][aj]=min(a[bj][aj],wj);//据说是防止出现aj到bj有两条路的情况呀
        //记录从aj到bj有一条路径，从bj到aj有一条路径（因为 双向通行）
    }
    for(int i=;i<=n;i++)
    {
        a[i][i]=;//自己到自己显然有一条为0的最短路
        t[i]=i;//这里好像是防止排序后找不到哪个是哪个下标吧？？
    }
    sort(t+,t++n,cmp);
    for(int i=;i<=n;i++)
        for(int j=;j<=n;j++)
            f[i][j]=a[i][j]+max(p[i],p[j]);//先初始化最短路为这两点间的距离+这两点中p较大的p值
    for(int k=;k<=n;k++)//floyd
        for(int i=;i<=n;i++)
            for(int j=;j<=n;j++)
            {
                a[i][j]=min(a[i][j],a[i][t[k]]+a[t[k]][j]);//干求最短路
                f[i][j]=min(f[i][j],a[i][j]+max(p[i],max(p[j],p[t[k]])));
            }
    for(int i=;i<=q;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",f[x][y]);
    }
    return ;
}

nice end-