P2496 [SDOI2012]体育课

传送门

分块

对每个块维护一个 $add$ 和 $del$ 标记，对于块 $o$ 内某个位置 $i$，它真实的修改量为 $a[i]+add[o]*i-del[o]$

这样就可以维护一个区间加一个等差数列的操作了

对于操作 $2$，交换两个位置，直接把两个位置的块标记下传，然后直接交换

对于操作 $1$，考虑到相同的块内 $add$ 只会越来越大，对于某个位置 $i$，它一开始是最大的位置，随着标记的增加，比它大的位置显然一定在它右边

所以考虑维护一个数列，使得数列相邻两个位置中，一旦左边的被超越，下一个可能的最大值就是右边下一个

我一开始天真地以为直接维护一个单调数列即可，然后搞了半天发现是错的，如图：

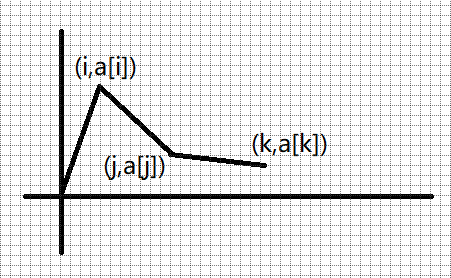
对于这种情况，当 $a[j]$ 还没超过 $a[i]$ 时，$a[k]$ 可能已经超过 $a[i]$ 了，所以我们不能把 $a[j]$ 放到数列里，不然就无法保证单调性

事实上，我们需要维护的是所有点对 $(x,a[x])$ 构成的上凸包，具体理由如下：

对于某个位置 $i$，如果 $a[i]$ 被超越，那么对于下一个位置 $k$ ，$i,k$ 之间必须不存在 $j$，使得

$a[i]+add*i-del>a[j]+add*j-del$ 并且 $a[k]+add*k-del>a[i]+add*i-del$

即 $(a[i]-a[j])/(i-j)<-add$ 且 $(a[i]-a[k])/(i-k)>-add$

即 $(a[i]-a[k])/(i-k)>(a[i]-a[j])/(i-j)$，发现左右两边其实就是连线的斜率，所以即维护一个上凸包

具体实现起来还是有一些细节的

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=2e5+,M=;
int n,m;
int bel[N],L[M],pos[M];
ll a[N],add[M],del[M];
vector <int> st[M];
inline void push_down(int o)
{
    for(int i=L[o];i<L[o+];i++) a[i]+=add[o]*i-del[o];
    add[o]=del[o]=pos[o]=; st[o].clear();
}
inline ll calc(int i,int o) { return a[i]+add[o]*i-del[o]; }
inline void upd(int o)
{
    while(pos[o]<st[o].size()- && calc(st[o][pos[o]],o)<=calc(st[o][pos[o]+],o)  ) pos[o]++;
}
inline void build(int o)
{
    for(int i=L[o];i<L[o+];st[o].push_back(i),i++)
        while(st[o].size()> &&
        (a[i]-a[st[o][st[o].size()-]])*(st[o][st[o].size()-]-st[o][st[o].size()-]) >=
        (a[st[o][st[o].size()-]]-a[st[o][st[o].size()-]])*(i-st[o][st[o].size()-]) ) st[o].pop_back();
    upd(o);
}
inline void query(int l,int r)
{
    int bl=bel[l-]+,br=bel[r+]-; ll res=;
    if(bl>br)
    {
        for(int i=l;i<=r;i++) res=max(res, calc(i,bel[i]) );
        printf("%lld\n",max(0ll,res-calc(,))); return;
    }
    for(int i=l;i<L[bl];i++) res=max(res, calc(i,bel[i]) );
    for(int i=L[br+];i<=r;i++) res=max(res, calc(i,bel[i]) );
    for(int i=bl;i<=br;i++) res=max(res, calc(st[i][pos[i]],i) );
    printf("%lld\n",max(0ll,res-calc(,)));
}
inline void Swap(int x,int y)
{
    push_down(bel[x]); push_down(bel[y]);
    swap(a[x],a[y]);
    build(bel[x]); build(bel[y]);
}
inline void change(int l,int r,int t)
{
    int bl=bel[l-]+,br=bel[r+]-;
    if(bl>br)
    {
        push_down(bel[l]); push_down(bel[r]);
        for(int i=l;i<=r;i++) a[i]+=1ll*(i-l+)*t;
        build(bel[l]); build(bel[r]); return;
    }
    if(L[bl]!=l)
    {
        for(int i=l;i<L[bl];i++) a[i]+=1ll*(i-l+)*t;
        push_down(bl-); build(bl-);
    }
    if(L[br+]-!=r)
    {
        for(int i=L[br+];i<=r;i++) a[i]+=1ll*(i-l+)*t;
        push_down(br+); build(br+);
    }
    for(int i=bl;i<=br;i++) add[i]+=t,del[i]+=1ll*(l-)*t,upd(i);
}
int main()
{
    n=read(),m=read(); int T=sqrt(n)+;
    for(int i=;i<=n;i++)
    {
        a[i]=read(); bel[i]=(i-)/T+;
        if(bel[i]!=bel[i-]) L[bel[i]]=i;
    }
    bel[n+]=bel[n]+; L[bel[n+]]=n+;
    for(int i=;i<=bel[n];i++) build(i);
    int opt,a,b;
    for(int i=;i<=m;i++)
    {
        opt=read(); a=read(),b=read();
        if(opt==) { query(a,b); continue; }
        if(opt==) { Swap(a,b); continue; }
        change(a,b,read());
    }
    return ;
}