[IOI1998]Polygon（区间dp）

[IOI1998]Polygon

题意翻译

多边形是一个玩家在一个有n个顶点的多边形上的游戏，如图所示，其中n＝4。每个顶点用整数标记，每个边用符号+（加）或符号*（乘积）标记。

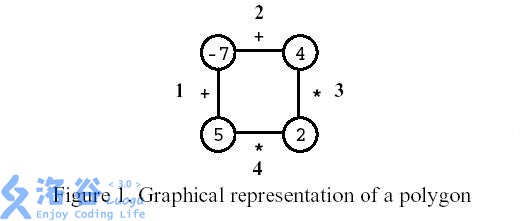
第一步，删除其中一条边。随后每一步：

选择一条边连接的两个顶点V1和V2，用边上的运算符计算V1和V2得到的结果来替换这两个顶点。

游戏结束时，只有一个顶点，没有多余的边。

如图所示，玩家先移除编号为3的边。之后，玩家选择计算编号为1的边，然后计算编号为4的边，最后，计算编号为2的边。结果是0。

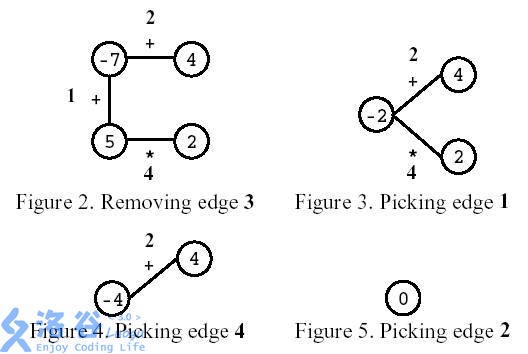
（翻译者友情提示：这里每条边的运算符旁边的数字为边的编号，不拿来计算）

编写一个程序，给定一个多边形，计算最高可能的分数。

输入格式

输入描述一个有n个顶点的多边形，它包含两行。第一行是数字n，为总边数。

第二行描述这个多边形，一共有2n个读入，每两个读入中第一个是字符，第二个是数字。

第一个字符为第一条边的计算符号(t代表相加，x代表相乘)，第二个代表顶点上的数字。首尾相连。

3 < = n < = 50

对于任何一系列的操作，顶点数字都在[-32768,32767]的范围内。

输出格式

第一行，输出最高的分数。在第二行，它必须写出所有可能的被清除后的边仍能得到最高得分的列表，必须严格递增。

一道区间dp很好的题目，很容易想到这样定义状态：\(F[i][j]\)表示把顶点\(i\)到\(j\)合并起来所获得的最大得分。但是发现顶点数据的范围可以为负数，而最大值可能由两个负数乘得(很容易忽略的点，做题要考虑周全)，所以我们需要同时记录最大值和最小值。由此\(F[i][j][0]\)表示把顶点\(i\)到\(j\)合并起来所获得的最小得分，\(F[i][j][1]\)表示把顶点\(i\)到\(j\)合并起来所获得的最大得分。

然后也许会想到直接去枚举断掉哪条边，但我们可以优化一下，像处理环状一样把链复制一遍到后面，因为每次断掉边之后就变成了链，所以我们可以一次处理出断掉每条边的值。

注意初始化

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
int read()
{
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0') {if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return x*w;
}
int n;
int c[1100],a[1100],team[1100];
int f[310][310][2];
void work1(int i,int j,int k)
{
    f[i][j][1]=max(f[i][j][1],f[i][k][1]+f[k+1][j][1]);
    f[i][j][0]=min(f[i][j][0],f[i][k][0]+f[k+1][j][0]);
}
void work2(int i,int j,int k)
{
    f[i][j][1]=max(f[i][j][1],max(f[i][k][1]*f[k+1][j][1],f[i][k][0]*f[k+1][j][0]));
    f[i][j][0]=min(f[i][j][0],min(min(f[i][k][0]*f[k+1][j][0],f[i][k][1]*f[k+1][j][0]),f[i][k][0]*f[k+1][j][1]));
}
void init()
{
    for(int i=1;i<=2*n;i++)
    {
        for(int j=i;j<=2*n;j++)
        f[i][j][1]=-20000000,f[i][j][0]=20000000;
    }
    for(int i=1;i<=n;i++)
    {
        f[i][i][1]=f[i][i][0]=a[i];
        f[i+n][i+n][1]=f[i+n][i+n][0]=a[i];
    }
}
int main()
{
    char ch;
    int cnt=0,ans=-20000000;
    n=read();
    for(int i=1;i<=n;i++)
    {
        cin>>ch;
        if(ch=='t') c[i]=1;
        if(ch=='x') c[i]=2;
        a[i]=read();
        a[i+n]=a[i];c[i+n]=c[i];
    }
    init();
    for(int l=2;l<=n;l++)
    {
        for(int i=1;i<=2*n;i++)
        {
            int j=i+l-1;
            for(int k=i;k<j;k++)
            {
                if(c[k+1]==1) work1(i,j,k);
                else work2(i,j,k);
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(f[i][i+n-1][1]>ans)
        {
            ans=f[i][i+n-1][1];
            cnt=0;
            team[++cnt]=i;
        }
        else if(f[i][i+n-1][1]==ans) team[++cnt]=i;
    }
    cout<<ans<<endl;
    for(int i=1;i<=cnt;i++)
    {
        cout<<team[i]<<" ";
    }
}