【图形学手记】Inverse Transform Sampling 逆转换抽样

需求：

我们通过调查，得知大多数人在20岁左右初恋，以20岁为基准，以随机变量X表示早于或晚于该时间的年数，为了简单，假设X值域为[-5,5]，并且PDF(X)是一个正态分布函数（当然可以为任意分布，这里具体化一个熟悉的，方便后面验证）

现在要求，做出一个计算机模拟程序，该程序能算出一系列X的值，并且这些值是符合观测所得的PDF(X)的

困难：

1.我们不可能有现成的函数，能够直接生成一系列值并且符合该分布。（虽然例子中指定了正态分布，但现实情况是任何分布都有可能，所以即使C++支持一系列分布函数，也不能解决本质问题）

2.难以求得一个函数的逆函数（至少我不知道怎么求。。至于为什么要求这个，下面会解释）

思路

1.得到一个均匀分布的，值域为[0,1]之间的随机函数并不困难，linux环境下有drand48()可用，windows下可借助于rand()实现；假设随机数为 r

2.可由PDF(X)得到CDF(X)

3.CDF(X)的值域是[0,1]，CDF^-1(X)的定义域是[0,1]，如果我们可以得到CDF的逆函数，就可以直接通过该函数得到想要的结果

3.将CDF的定义域，也就是[-5,5]，分成32段，定义为一个数组，假设数组名为cdfs，得到cdfs长度为33 ，其中cdfs[0] = 0，cdfs[32]=1

4.找到cdfs(i)，使得cdfs(i）是升序排列后找到的，大于等于r的cdfs数组中的最小值，如果没有找到的话，就返回cdfs(32)，也就是1

5.假设找到的i = 15，此时情况如下图

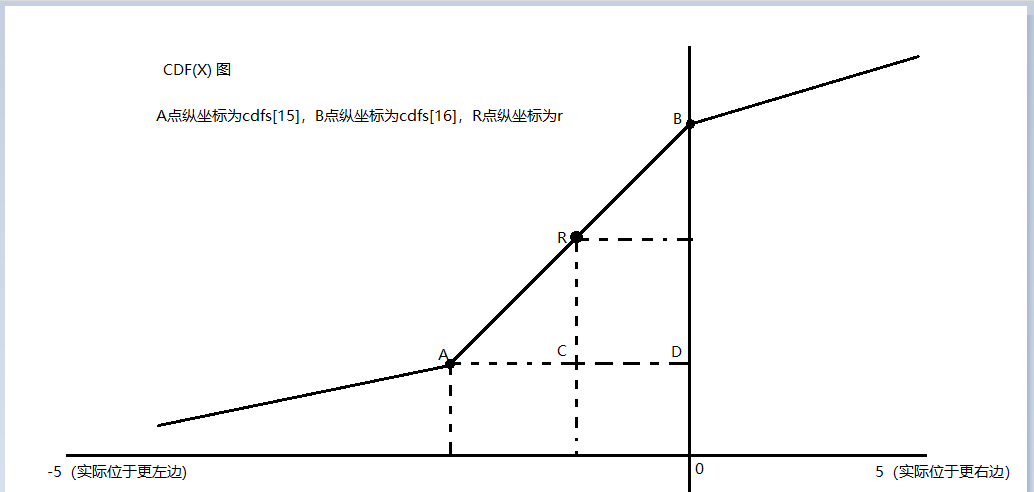
显然我们只需要知道AC的长度即可得到随机变量X的取值，假设该值为x，则 x = A点的横坐标 + AC的长度

由于A点是第15个点，所以 x = -5 + (10/32)*15 + AC

而由于 AC / AD = RC / BD，所以 AC = RC * AD / BD

其中，RC = r - cdfs[15] ， AD = B点横坐标 -  A点横坐标，也就是一个dx的长度，即 (10/32)，BD = B点纵坐标 - A点纵坐标 = cdfs[16] - cdfs[15]

这样就得出x了

大体思路就是如此，以下是简陋的代码实现，C++基本属于不会用，后面会持续改进这个例子

#include <iostream>
#include <random>
#define M_PI 3.14159265358979323846
 
using namespace std;
 
// 产生0~1之间的随机数
double randx() {
    random_device rd;
    default_random_engine gen{ rd() };
    uniform_real_distribution<> distr;
    return distr(gen);
}
 
// standard normal distribution function
float pdf(const float& x)
{
    return  / sqrtf( * M_PI) * exp(-x * x * 0.5);
}
 
// create CDF
// nbins 将cdf分成多少段
// minBound 下限
// maxBound 上限
float* cdfCreator(const int nbins, float minBound, float maxBound) {
 
    // cdf容量是要比nbin多1的;试想如果nbins=2,也就是说把[-5,5]分成2段，结果对CDF来说形成了3个节点，分别是-5,0,5
    //float cdf[nbins + 1], dx = (maxBound - minBound) / nbins, sum = 0;
    float* cdf = new float[nbins + ];
    float dx = (maxBound - minBound) / nbins;
    cdf[] = ;
    cdf[nbins] = ;
    for (int n = ; n < nbins; n++) {
        float x = minBound + (maxBound - minBound) * (n / (float)(nbins));
        // 计算dx这一小块对应的概率
        float pdf_x = pdf(x) * dx;
        cdf[n] = cdf[n - ] + pdf_x;
    }
 
    // 调试信息
    cout << "[DEBUG] cdf: ";
    for (int i = ; i < ; i++) {
        cout << "cdf[" << i << "]: " << cdf[i] << endl;
    }
 
    return cdf;
}
 
float sample(float* cdf, const uint32_t & nbins, const float& minBound, const float& maxBound)
{
    float r = randx();
    float dx = (maxBound - minBound) / nbins;
 
    // 从cdf开始，到cdf+nbins+1为止，找到第一个大于或等于r的值，在这个例子中，cdf+nbins=32，也就是cdf[32]，即cdf数组的最后一个元素
    // 得到的ptr指向从cdf[0]到cdf[32]中随机的一个元素的地址
    // 由于后买计算bd时用到了off+1，为了不越界，所以off最大只能为31，所以ptr最大能取第cdf[31]的地址，所以下面要-1
    float* ptr = std::lower_bound(cdf, cdf + nbins - , r);
 
    // 由于lower_bound的性质，cdf[ptr-cdf]永远是大于r的，为了符合我们上文的构思，这里就进行减一处理，对应于上图，off是15而不是16
    int off = ptr - cdf - ;
 
    float rc = r - cdf[off];
    float ad = dx;
    float bd = cdf[off + ] - cdf[off];
    float ac = rc * ad / bd;
    float x = minBound + dx * off + ac;
    return x;
}
 
int main(int argc, char** argv)
{
    // create CDF
    const int nbins = ;
    float minBound = -, maxBound = ;
    float* cdf = cdfCreator(nbins, minBound, maxBound);
 
    // our simulation
    int numSims = ; //样本容量10万
    const int numBins = ; // to collect data on our sim
    int bins[numBins]; // to collect data on our sim
    memset(bins, 0x0, sizeof(int) * numBins); // set all the bins to 0 ，将bins的前sizeof(int)*numBins个字节全部设置值为0x0
 
    for (int i = ; i < numSims; i++) { // 抽样十万
        float x = sample(cdf, nbins, minBound, maxBound); // random var between -5 and 5 
 
        //计算x落在了我们自己定义的哪个分段里
        int whichBin = (int)((numBins - ) * (x - minBound) / (maxBound - minBound));
        bins[whichBin]++;
    }
 
    // 输出bins看看对不对
    for (int i = ; i < numBins; i++) {
        /*float r = bins[i] / (float)numSims;
        printf("%f %f\n", 5 * (2 * (i / (float)(numBins)) - 1), r);
        cout << "[debug]i: " << i << endl;*/
        cout << "bins[" << i << "]: " << bins[i] << endl;
    }
 
    delete cdf;
    return ;
}

运行结果：像是那么回事

bins[0]: 0
bins[1]: 0
bins[2]: 1
bins[3]: 0
bins[4]: 0
bins[5]: 0
bins[6]: 2
bins[7]: 0
bins[8]: 1
bins[9]: 2
bins[10]: 5
bins[11]: 7
bins[12]: 6
bins[13]: 7
bins[14]: 13
bins[15]: 28
bins[16]: 34
bins[17]: 34
bins[18]: 52
bins[19]: 95
bins[20]: 92
bins[21]: 92
bins[22]: 166
bins[23]: 163
bins[24]: 239
bins[25]: 391
bins[26]: 366
bins[27]: 426
bins[28]: 705
bins[29]: 724
bins[30]: 719
bins[31]: 1200
bins[32]: 1150
bins[33]: 1191
bins[34]: 1793
bins[35]: 1861
bins[36]: 1916
bins[37]: 2504
bins[38]: 2557
bins[39]: 2630
bins[40]: 3243
bins[41]: 3278
bins[42]: 3316
bins[43]: 3811
bins[44]: 3896
bins[45]: 3857
bins[46]: 3811
bins[47]: 4013
bins[48]: 4150
bins[49]: 3827
bins[50]: 3830
bins[51]: 3803
bins[52]: 3542
bins[53]: 3287
bins[54]: 3315
bins[55]: 3029
bins[56]: 2618
bins[57]: 2590
bins[58]: 2474
bins[59]: 1882
bins[60]: 1832
bins[61]: 1735
bins[62]: 1171
bins[63]: 1176
bins[64]: 1191
bins[65]: 722
bins[66]: 705
bins[67]: 665
bins[68]: 379
bins[69]: 321
bins[70]: 382
bins[71]: 213
bins[72]: 185
bins[73]: 164
bins[74]: 97
bins[75]: 88
bins[76]: 75
bins[77]: 39
bins[78]: 30
bins[79]: 33
bins[80]: 21
bins[81]: 7
bins[82]: 6
bins[83]: 7
bins[84]: 3
bins[85]: 3
bins[86]: 3
bins[87]: 1
bins[88]: 0
bins[89]: 2
bins[90]: 0
bins[91]: 0
bins[92]: 0
bins[93]: 0
bins[94]: 0
bins[95]: 0
bins[96]: 0
bins[97]: 0
bins[98]: 0
bins[99]: 0