Nowcoder Sum of Maximum ( 容斥原理 && 拉格朗日插值法 )

题目链接

题意 :

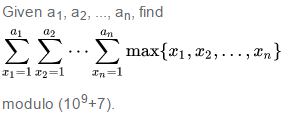
分析 :

分析就直接参考这个链接吧 ==> Click here

大体的思路就是

求和顺序不影响结果、故转化一下思路枚举每个最大值对答案的贡献最后累加就是结果

期间计数的过程要用到容斥和多项式求和 ( 利用拉格朗日求即可 ) 具体参考给出的链接

#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long

#define scl(i) scanf("%lld", &i)
#define scll(i, j) scanf("%lld %lld", &i, &j)
#define sclll(i, j, k) scanf("%lld %lld %lld", &i, &j, &k)
#define scllll(i, j, k, l) scanf("%lld %lld %lld %lld", &i, &j, &k, &l)

#define scs(i) scanf("%s", i)
#define sci(i) scanf("%d", &i)
#define scd(i) scanf("%lf", &i)
#define scIl(i) scanf("%I64d", &i)
#define scii(i, j) scanf("%d %d", &i, &j)
#define scdd(i, j) scanf("%lf %lf", &i, &j)
#define scIll(i, j) scanf("%I64d %I64d", &i, &j)
#define sciii(i, j, k) scanf("%d %d %d", &i, &j, &k)
#define scddd(i, j, k) scanf("%lf %lf %lf", &i, &j, &k)
#define scIlll(i, j, k) scanf("%I64d %I64d %I64d", &i, &j, &k)
#define sciiii(i, j, k, l) scanf("%d %d %d %d", &i, &j, &k, &l)
#define scdddd(i, j, k, l) scanf("%lf %lf %lf %lf", &i, &j, &k, &l)
#define scIllll(i, j, k, l) scanf("%I64d %I64d %I64d %I64d", &i, &j, &k, &l)

#define lson l, m, rt<<1
#define rson m+1, r, rt<<1|1
#define lowbit(i) (i & (-i))
#define mem(i, j) memset(i, j, sizeof(i))

#define fir first
#define sec second
#define VI vector<int>
#define ins(i) insert(i)
#define pb(i) push_back(i)
#define pii pair<int, int>
#define VL vector<long long>
#define mk(i, j) make_pair(i, j)
#define all(i) i.begin(), i.end()
#define pll pair<long long, long long>

#define _TIME 0
#define _INPUT 0
#define _OUTPUT 0
clock_t START, END;
void __stTIME();
void __enTIME();
void __IOPUT();
using namespace std;
;
;

LL pow_mod(LL a, LL b)
{
    a %= mod;
    LL ret = ;
    while(b){
        ) ret = (ret * a) % mod;
        a = ( a * a ) % mod;
        b >>= ;
    }
    return ret;
}

namespace polysum {
    #define rep(i,a,n) for (int i=a;i<n;i++)
    #define per(i,a,n) for (int i=n-1;i>=a;i--)
    ;
    LL a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][],C[D];
    LL powmod(LL a,LL b){LL res=;a%=mod;assert(b>=);){)res=res*a%mod;a=a*a%mod;}return res;}
    LL calcn(int d,LL *a,LL n) { // a[0].. a[d]  a[n]
        if (n<=d) return a[n];
        p1[]=p2[]=;
        rep(i,,d+) {
            LL t=(n-i+mod)%mod;
            p1[i+]=p1[i]*t%mod;
        }
        rep(i,,d+) {
            LL t=(n-d+i+mod)%mod;
            p2[i+]=p2[i]*t%mod;
        }
        LL ans=;
        rep(i,,d+) {
            LL t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod;
            ) ans=(ans-t+mod)%mod;
            else ans=(ans+t)%mod;
        }
        return ans;
    }
    void init(int M) {
        f[]=f[]=g[]=g[]=;
        rep(i,,M+) f[i]=f[i-]*i%mod;
        g[M+]=powmod(f[M+],mod-);
        per(i,,M+) g[i]=g[i+]*(i+)%mod;
    }
    LL polysum(LL m,LL *a,LL n) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]
        LL b[D];
        ;i<=m;i++) b[i]=a[i];
        b[m+]=calcn(m,b,m+);
        rep(i,,m+) b[i]=(b[i-]+b[i])%mod;
        ,b,n-);
    }
    LL qpolysum(LL R,LL n,LL *a,LL m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i
        ) return polysum(n,a,m);
        a[m+]=calcn(m,a,m+);
        LL r=powmod(R,mod-),p3=,p4=,c,ans;
        h[][]=;h[][]=;
        rep(i,,m+) {
            h[i][]=(h[i-][]+a[i-])*r%mod;
            h[i][]=h[i-][]*r%mod;
        }
        rep(i,,m+) {
            LL t=g[i]*g[m+-i]%mod;
            ) p3=((p3-h[i][]*t)%mod+mod)%mod,p4=((p4-h[i][]*t)%mod+mod)%mod;
            ]*t)%mod,p4=(p4+h[i][]*t)%mod;
        }
        c=powmod(p4,mod-)*(mod-p3)%mod;
        rep(i,,m+) h[i][]=(h[i][]+h[i][]*c)%mod;
        rep(i,,m+) C[i]=h[i][];
        ans=(calcn(m,C,n)*powmod(R,n)-c)%mod;
        ) ans+=mod;
        return ans;
    }
}

LL arr[maxn];
int main(void){__stTIME();__IOPUT();

    int n;
    polysum::init(maxn);
    while(~sci(n)){
        ; i<=n; i++) scl(arr[i]);

        sort(arr+, arr++n);

        arr[] = ;

        LL now = ;

        LL b[maxn];

        LL ans = ;
        ; i<=n; i++){
            ]){
                now = (now * arr[i]) % mod;
                continue;
            }
            b[] = ;
            ; j<=n-i+; j++)
                b[j] = (LL)j * ((pow_mod((LL)j, n-i+) - pow_mod((LL)j-1LL, n-i+)%mod)+mod)%mod;
            LL tmp = ((polysum::polysum(n-i+, b, arr[i]+) -
                       polysum::polysum(n-i+, b, arr[i-]+)%mod)+mod)%mod;

            ans = (ans + (tmp%mod * now%mod)%mod)%mod;

            now = (now * arr[i]) % mod;
        }

        printf("%lld\n", ans);
    }

__enTIME();;}

void __stTIME()
{
    #if _TIME
        START = clock();
    #endif
}

void __enTIME()
{
    #if _TIME
        END = clock();
        cerr<<"execute time = "<<(double)(END-START)/CLOCKS_PER_SEC<<endl;
    #endif
}

void __IOPUT()
{
    #if _INPUT
        freopen("in.txt", "r", stdin);
    #endif
    #if _OUTPUT
        freopen("out.txt", "w", stdout);
    #endif
}

注 :

N + 1 个点能确定一个 N 次多项式、故拉格朗日插值需要确定 ( 最高次次数 + 1 ) 个点的值

namespace polysum {
    #define rep(i,a,n) for (int i=a;i<n;i++)
    #define per(i,a,n) for (int i=n-1;i>=a;i--)
    ;//可能需要用到的最高次
    LL a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][],C[D];
    LL powmod(LL a,LL b){LL res=;a%=mod;assert(b>=);){)res=res*a%mod;a=a*a%mod;}return res;}
    LL calcn(int d,LL *a,LL n) { // a[0].. a[d]  a[n]
        if (n<=d) return a[n];
        p1[]=p2[]=;
        rep(i,,d+) {
            LL t=(n-i+mod)%mod;
            p1[i+]=p1[i]*t%mod;
        }
        rep(i,,d+) {
            LL t=(n-d+i+mod)%mod;
            p2[i+]=p2[i]*t%mod;
        }
        LL ans=;
        rep(i,,d+) {
            LL t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod;
            ) ans=(ans-t+mod)%mod;
            else ans=(ans+t)%mod;
        }
        return ans;
    }
    void init(int M) {//用到的最高次
        f[]=f[]=g[]=g[]=;
        rep(i,,M+) f[i]=f[i-]*i%mod;
        g[M+]=powmod(f[M+],mod-);
        per(i,,M+) g[i]=g[i+]*(i+)%mod;
    }
    LL polysum(LL m,LL *a,LL n) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]
        ;i<=m;i++) b[i]=a[i];
        b[m+]=calcn(m,b,m+);
        rep(i,,m+) b[i]=(b[i-]+b[i])%mod;
        ,b,n-);
    }
    LL qpolysum(LL R,LL n,LL *a,LL m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i
        ) return polysum(n,a,m);
        a[m+]=calcn(m,a,m+);
        LL r=powmod(R,mod-),p3=,p4=,c,ans;
        h[][]=;h[][]=;
        rep(i,,m+) {
            h[i][]=(h[i-][]+a[i-])*r%mod;
            h[i][]=h[i-][]*r%mod;
        }
        rep(i,,m+) {
            LL t=g[i]*g[m+-i]%mod;
            ) p3=((p3-h[i][]*t)%mod+mod)%mod,p4=((p4-h[i][]*t)%mod+mod)%mod;
            ]*t)%mod,p4=(p4+h[i][]*t)%mod;
        }
        c=powmod(p4,mod-)*(mod-p3)%mod;
        rep(i,,m+) h[i][]=(h[i][]+h[i][]*c)%mod;
        rep(i,,m+) C[i]=h[i][];
        ans=(calcn(m,C,n)*powmod(R,n)-c)%mod;
        ) ans+=mod;
        return ans;
    }
}

拉格朗日插值模板 (dls版)

-------------------------------分 割 线-------------------------------

链接题解用到的化简容斥的多项式展开式如下

( x - 1 ) ^ k

= x^k

+ C(k, 1) * x^(k-1) * (-1)^1

+ C(k, 2) * x^(k-2) * (-1)^2

+ ......

+ C(k, k) * x^(k-k) * (-1)^k