【CF 482E】ELCA

题意

　　

　　

　　

题解

50pts

　　由于这题 \(2s\)，所以可以信仰一波，暴力修改、查询。

　　暴力修改的复杂度是 \(O(n)\)，暴力查询的复杂度是 \(O(n^2)\)。

　　但不难发现可以通过记录子树大小来优化查询。具体地就是我们发现可以从每个点出发走到根，每经过一个点就计算一下起点与多少个点的 \(\text{LCA}\) 是这个点。预处理一下以每个点为根的子树大小即可。

　　优化一下，我们发现直接 \(\text{dfs}\) 一遍整颗树就能统计所有答案。对于每个点 \(u\) 枚举一条儿子边，设该儿子边指向的儿子为 \(v\)，然后令第一只虫子在以 \(v\) 为根的子树内，第二只虫子在以 \(u\) 为根的子树内且不在以 \(v\) 为根的子树内，此时有 \(size[v]\times (size[u]-size[v])\) 对点的 \(\text{LCA}\) 为 \(u\)，所以答案要累加 \(size[v]\times (size[u]-size[v])\times a[u]\)。这样我们就漏掉了第一支虫子在 \(u\) 上的情况，最后再把答案加 \(size[u]\times a[u]\) 即可。

　　于是查询的复杂度优化到了 \(O(n)\)，总复杂度 \(O(n^2)\)。

　　然而我 \(O(n^3)\) 的暴力过了 \(\text{50pts}\)……下面是我的 \(\text{code}\)

#include<bits/stdc++.h>
#define ll long long
#define N 100010
using namespace std;
inline int read(){
	int x=0; bool f=1; char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=0;
	for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0';
	if(f) return x;
	return 0-x;
}

int n,m,a[N];
struct edge{int v,nxt; bool fx,exist;}e[N<<3];
int hd[N],cnt;
inline void add(int u, int v, bool fx){e[cnt]=(edge){v,hd[u],fx,1}, hd[u]=cnt++;}
int fa[N],siz[N];

double ans;
void getSiz(int u){
	siz[u]=1;
	for(int i=hd[u]; ~i; i=e[i].nxt) if(e[i].exist && !e[i].fx) getSiz(e[i].v), siz[u]+=siz[e[i].v];
	//cout<<u<<' '<<siz[u]<<endl;
}
void dfs(int u, int f){
	//cout<<a[u]<<' '<<siz[u]-siz[fa]<<endl;
	ans += 1ll * a[u] * (siz[u]-siz[f]);
	if(fa[u]) dfs(fa[u],u);
}
double getAns(){
	ans=0;
	for(int i=1; i<=n; ++i) dfs(i,0);
	//cout<<ans<<endl;
	return ans/=(ll)n*n;
}
int main(){
	n=read();
	int u,v;
	memset(hd,-1,sizeof hd);
	for(int i=2; i<=n; ++i) fa[i]=read(), add(fa[i],i,0), add(i,fa[i],1);
	for(int i=1; i<=n; ++i) a[i]=read();
	getSiz(1);
	printf("%.10lf\n",getAns());
	m=read();
	int opt;
	for(int i=1; i<=m; ++i){
		opt=read(), u=read(), v=read();
		if(opt==1){
			int x=v; bool flag=0;
			while(x){
				x=fa[x];
				if(x==u){flag=1; break;}
			}
			if(flag) swap(u,v);

			x=fa[u];
			while(x){
				siz[x]-=siz[u];
				x=fa[x];
			}
			for(int j=hd[fa[u]]; ~j; j=e[j].nxt) if(e[j].exist && !e[j].fx && e[j].v==u){e[j].exist=e[j^1].exist=0; break;}

			fa[u]=v, add(v,u,0), add(u,v,1);
			//getSiz(1);
			x=v;
			while(x){
				siz[x]+=siz[u];
				x=fa[x];
			}
		}
		else a[u]=v;
		printf("%.10lf\n",getAns());
	}
	return 0;
}

70pts（CF 原题标算）

　　分块。

100pts

　　显然 LCT。

　　回头考虑 \(\text{50pts}\) 做法，它的式子可以简化！

　　一个点对答案的贡献是

　　\(\{\sum\limits_v size[v]\times (size[u]-size[v])+size[u]\}\times a[u]\)（\(v\) 是 \(u\) 的儿子）

　　\(=\{(size[u]\times \sum\limits_v size[v]) - \sum\limits_v size[v]^2 + size[u]\}\times a[u]\)

　　\(=\{size[u]\times (size[u]-1) - \sum\limits_v size[v]^2 + size[u]\}\times a[u]\)

　　\(=\{size[u]^2 - \sum\limits_v size[v]^2\}\times a[u]\)

　　那我们是不是可以在 LCT 的每个点上维护这个答案？

　　下面考虑一下需要维护哪些信息

　　首先 LCT 上每个点肯定要维护该点及所有虚子树的 \(size\) 和，设其为 \(siz\)。

　　然后我们需要维护该点及所有实子树的 \(size\) 和，设其为 \(siz_sum\)。

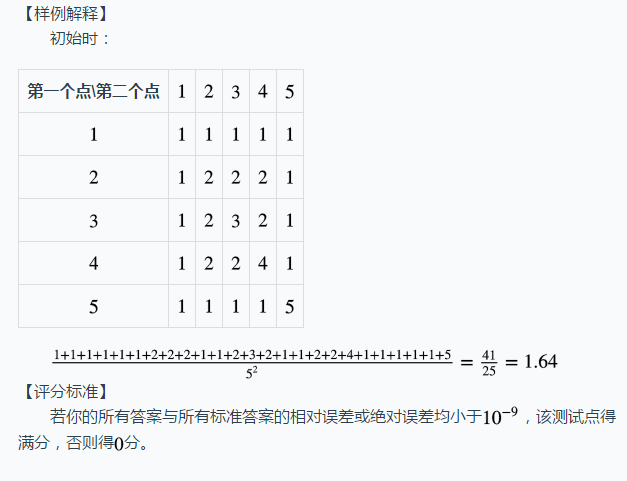
　　注意：大家都知道虚子树包括所有实边连接的后代，但可能在实子树是否包含虚边连接后代这个问题有歧义。这里规定，实子树也包括所有虚边连接的后代！比如这张图（实线表示实边，虚线表示虚边）

　　

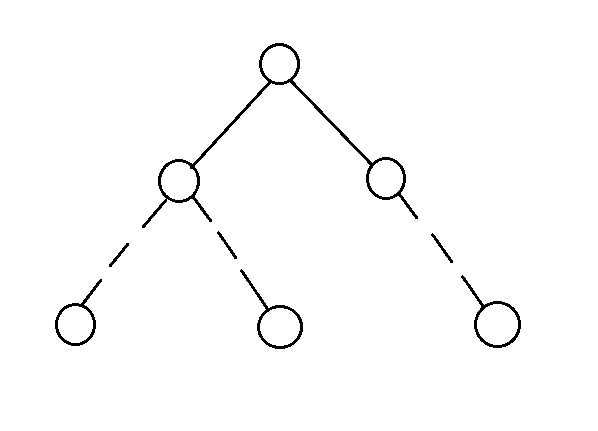
　　这 \(6\) 个点是一棵实子树，而不是只有上面 \(3\) 个点组成一棵实子树！

　　在下文中，如果要指上面 \(3\) 个点组成的子树，我们称其为 在 splay 上的某个子树。

　　然后我们需要记录虚子树大小平方和，用于计算该点对答案的贡献，设其为 \(siz\_sqr\)。

　　然后我们需要统计整棵树的答案，所以需要把子树的答案往父亲合并，于是记录虚子树 \(ans\) 和，设其为 \(ans\_sum\)。

　　用 \(siz\_sum\) 和 \(ans\_sum\) 即可算出 splay 中以这个点为根的子树中所有点对答案的贡献和，记其为 \(ans\)。

　　然后我们画个图，尝试合并一下

　　

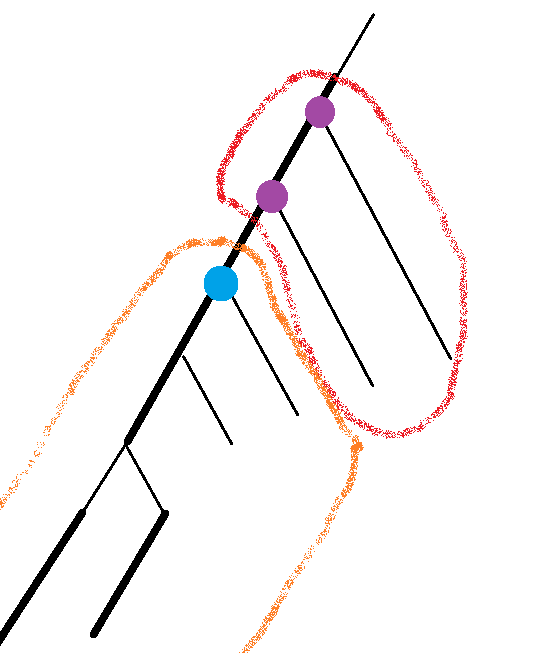
　　图中粗线为重链，细线为轻链，蓝色点表示维护重链的 splay 的根（为了理解方便就直接设成了根，其实设成 splay 里的任意一个非叶子节点都行）。

　　合并的时候，发现若一只虫子在蓝色节点的右实子树中（即橙色圈圈区域），另一只虫子在蓝色节点的左实子树中（即红色圈圈区域），那这两点的 \(\text{LCA}\) 并不是蓝色节点，而是其在 splay 上的左子树中的点。不难发现，这种情况下左子树上的某个点为两点的 \(\text{LCA}\)，当且仅当有一个点在该点的虚子树中。所以我们再给每个点记录一个变量 \(all\)，表示 splay 中以它为根的子树中，所有点的 \(siz\times a[k]\) 之和（设点编号为 \(k\)）。

　　\(\text{pushup}\) 时，一个点的 \(ans\) 需要考虑较多因素，即更新成以下几项的和：

• 两个实子树和所有虚子树的 \(ans\)
• 两只虫子分别在两个不同的虚子树中
• 一只虫子在任一虚子树中，另一只虫子在右实子树中。这时交换两只虫子后的方案没被统计，所以方案数 \(\times\space 2\)
• 一只虫子在任一虚子树或右实子树中，另一只虫子在左实子树中。这时交换两只虫子后的方案没被统计，所以方案数 \(\times\space 2\)

　　显然，后三条都是计算该点对答案的贡献，即有多少对点以这个点为 \(\text{LCA}\)。

　　然后就可以写成如下代码的 \(\text{pushup}\) 了。

　　

　　注意一个细节：一般我们写 LCT 维护的都是无根树，但这题 LCT 护的是有根树，所以 \(\text{makeroot}\) 函数不要翻转子树（这会修改树根）。

　　取答案的话，直接取 LCT 最顶部节点的 \(ans\) 即可。如果你不知道顶部节点的编号，随便把一个节点 \(\text{makeroot}\) 一下旋转到顶部就行了。

#include<bits/stdc++.h>
#define ll long long
#define N 100010
using namespace std;
inline int read(){
	int x=0; bool f=1; char c=getchar();
	for(;!isdigit(c); c=getchar()) if(c=='-') f=0;
	for(; isdigit(c); c=getchar()) x=(x<<3)+(x<<1)+(c^'0');
	if(f) return x;
	return 0-x;
}
int n,m,a[N];
namespace LCT{
	#define son(x,k) tr[x].son[k]
	struct Tree{
		int son[2],fa;
		ll siz,siz_sum,siz_sqr,ans_sum,all,ans;
	}tr[N];

	inline bool isRoot(int x){
		return son(tr[x].fa,0)!=x && son(tr[x].fa,1)!=x;
	}
	inline bool idf(int x){
		return son(tr[x].fa,1)==x;
	}
	void pushup(int x){
		tr[x].siz_sum = tr[son(x,0)].siz_sum + tr[son(x,1)].siz_sum + tr[x].siz;
		tr[x].ans = tr[son(x,0)].ans + tr[son(x,1)].ans + tr[x].ans_sum
				  + (1ll * tr[x].siz * tr[x].siz - tr[x].siz_sqr
				  + 2ll * tr[x].siz * tr[son(x,1)].siz_sum) * a[x]
				  + 2ll * tr[son(x,0)].all * (tr[x].siz_sum-tr[son(x,0)].siz_sum);
		tr[x].all = tr[son(x,0)].all + tr[son(x,1)].all + a[x] * tr[x].siz;
		//cout<<tr[x].siz_sum<<' '<<tr[x].ans<<' '<<tr[x].all<<endl;
	}
	void vir_pushup(int x, int y, int v){
		tr[x].siz += v * tr[y].siz_sum;
		tr[x].siz_sqr  += v * tr[y].siz_sum * tr[y].siz_sum;
		tr[x].ans_sum += v * tr[y].ans;
	}
	inline void connect(int x, int f, int fx){
		tr[x].fa=f, son(f,fx)=x;
	}
	inline void rotate(int x){
		int y=tr[x].fa, z=tr[y].fa, idf_x=idf(x), idf_y=idf(y), B=tr[x].son[idf_x^1];
		if(!isRoot(y)) connect(x,z,idf_y);
		else tr[x].fa=z;
		connect(B,y,idf_x), connect(y,x,idf_x^1);
		pushup(y), pushup(x);
	}
	void splay(int x){
		for(; !isRoot(x); ){
			int f=tr[x].fa;
		//cout<<"splay:"<<x<<' '<<f<<endl;
			if(!isRoot(f)) rotate(idf(x)==idf(f) ? f : x);
			rotate(x);
		}
	}
	void access(int x){
		for(int y=0; x; x=tr[y=x].fa){
			//cout<<x<<' '<<y<<endl;
			splay(x);
			vir_pushup(x,son(x,1),1);
			son(x,1)=y;
			vir_pushup(x,son(x,1),-1);
			pushup(x);
			//cout<<x<<' '<<y<<endl;
		}
	}
	inline void makeroot(int x){
		access(x), splay(x);
	}
	void link(int x, int y){
		//cout<<y<<endl;
		makeroot(y), makeroot(x);
		//cout<<y<<endl;
		tr[y].fa=x;
		vir_pushup(x,y,1), pushup(x);
	}
	void cut(int x, int y){
		makeroot(x), splay(y);
		tr[y].fa=0;
		vir_pushup(x,y,-1), pushup(x);
	}
	bool isAnc(int x, int y){ //判断x是不是y的祖先，是则返回1
		makeroot(y), splay(x);
		if(isRoot(y)) return 0;
		return 1;
	}
}using namespace LCT;
int fa[N];
int main(){
	n=read();
	for(int i=2; i<=n; ++i) fa[i]=read();
	for(int i=1; i<=n; ++i){
		a[i]=read();
		tr[i].all = tr[i].ans = a[i];
		tr[i].siz_sum = tr[i].siz = 1;
	}
	for(int i=2; i<=n; ++i) link(fa[i],i);
	access(1), splay(1);
	printf("%.10lf\n",(double)tr[1].ans/n/n);
	m=read();
	while(m--){
		int opt=read(), x=read(), y=read();
		if(opt==1){
			if(!isAnc(x,y)) cut(fa[x],x), link(y,x), fa[x]=y;
			else cut(fa[y],y), link(x,y),fa[y]=x;
			access(1), splay(1);
			printf("%.10lf\n",(double)tr[1].ans/n/n);
		}
		else{
			makeroot(x), a[x]=y, pushup(x);
			printf("%.10lf\n",(double)tr[x].ans/n/n);
		}
	}
	return 0;
}

　　过两天复习一波 LCT，这数据结构真是个害人不浅的东西