[luogu]P2680 运输计划[二分答案][树上差分]

[luogu]P2680

[NOIP2015]运输计划

题目背景

公元 2044 年,人类进入了宇宙纪元。

题目描述

L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物

流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道 是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之 间不会产生任何干扰。

为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的 物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段 性工作所需要的最短时间是多少?

输入输出格式

输入格式：

输入文件名为
transport.in。

第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。

接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第

i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。

接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个
运输计划是从 uj 号星球飞往 vj 号星球。

输出格式：

输出 共1行,包含1个整数,表示小P的物流公司完成阶段性工作所需要的最短时间。

输入输出格式

输入样例1#：

6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5

输出样例1#：

11

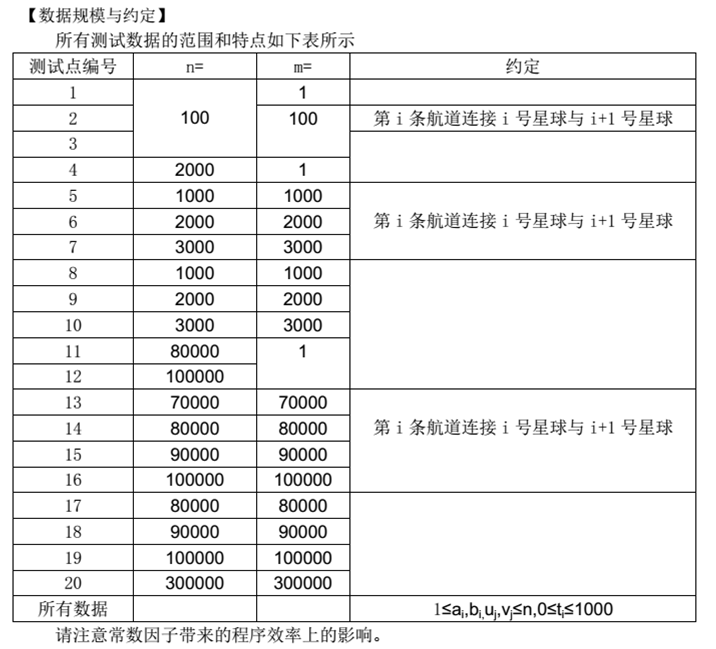
说明

---

题目大概就是要使一条边的权值变为零，使得选择的所有路径的长度值最大值最小。

考虑二分答案，但这个检验怎么搞啊？

对于一个二分长度mid，先把那些比它长的标记一下记录为num个，之后枚举每一条边，如果覆盖这条边的所有路径数为num，且这条边的权值>=（MAX-mid）。

然后我还是不会搞，所以去看大佬们写的题解，说是要树上差分，我*，这又是什么鬼，今天一定要好好学习一下，就拿这题练手。

对于一个（u，v）点对，f[u]++，f[v]++，f[lca（u，v）]-=2，这样一来如果对i的子树的f求和，得到的值就是（i，fa[i]）这条边被用了几次。

这样检验就能在O（n+m）完成。

lca我只会写树剖啊。

这数据是不是有点奇怪啊，我有一个点差点T了...（好把，其实应该是蒟蒻我太弱了~_~）

代码：

 //2017.11.2
 //tree 差分 二分
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 inline int read();
 int Max(int x,int y){return x>y?x:y;}
 ?x:-x;}
 namespace lys{
      ;
     struct edge{
         int to;
         int next;
         int w;
     }e[N*];
     int sum[N],f[N],pre[N],fa[N],siz[N],dep[N],top[N],lca[N],len[N],u[N],v[N],dis[N],d[N],son[N];
     bool used[N];
     int n,m,cnt,M;
     void add(int x,int y,int w){
         e[++cnt].to=y;e[cnt].next=pre[x];pre[x]=cnt;e[cnt].w=w;
         e[++cnt].to=x;e[cnt].next=pre[y];pre[y]=cnt;e[cnt].w=w;
     }
     void dfs1(int node,int deep){
         dep[node]=deep;
         siz[node]=;
         int i,v;
         for(i=pre[node];~i;i=e[i].next){
             v=e[i].to;
             if(v==fa[node]) continue ;
             fa[v]=node;
             d[v]=e[i].w;
             dfs1(v,deep+);
             siz[node]+=siz[v];
             if(siz[son[node]]<siz[v]) son[node]=v;
         }
     }
     void dfs2(int node,int tp,int ds){
         top[node]=tp;
         dis[node]=ds+d[node];
         if(!son[node]) return ;
         dfs2(son[node],tp,dis[node]);
         int i,v;
         for(i=pre[node];~i;i=e[i].next){
             v=e[i].to;
             if(v==fa[node]||v==son[node]) continue ;
             dfs2(v,v,);
         }
     }
     void LCA(int x,int y,int pos){
         int f1,f2;
         while(true){
             f1=top[x],f2=top[y];
             if(f1==f2){
                 if(dep[x]<dep[y]) lca[pos]=x;
                 else lca[pos]=y;
                 len[pos]+=ABS(dis[x]-dis[y]);
                 return ;
             }
             if(dep[f1]<dep[f2]){
                 len[pos]+=dis[y];
                 y=fa[f2];
             }
             else{
                 len[pos]+=dis[x];
                 x=fa[f1];
             }
         }
     }
     void dfs(int node){
         int i,v;
         sum[node]=f[node];
         f[node]=;
         for(i=pre[node];~i;i=e[i].next){
             v=e[i].to;
             if(v==fa[node]) continue ;
             dfs(v);
             sum[node]+=sum[v];
         }
     }
     bool chk(int mid){
         ;
         ;i<=m;i++) if(len[i]>mid) num++,used[i]=true ;
         ;i<=m;i++)
             ,used[i]=false ;
         dfs();
         ;i<=n;i++) if(sum[i]>=num&&d[i]>=(M-mid)) return true ;
         return false ;
     }
     int main(){
         int i,x,y,w;
         n=read(); m=read();
         memset(pre,-,sizeof pre);
         ;i<n;i++){
             x=read(); y=read(); w=read();
             add(x,y,w);
         }
         dfs1(,),dfs2(,,);
         ;i<=m;i++){
             u[i]=read(); v[i]=read();
             LCA(u[i],v[i],i);
             M=Max(M,len[i]);
         }
         ,r=M,mid;
         while(l<r){
             mid=(l+r)>>;
             if(chk(mid)) r=mid;
             ;
         }
         printf("%d\n",l);
         ;
     }
 }
 int main(){
     lys::main();
     ;
 }
 inline int read(){
     ,ff=;
     char c=getchar();
     '){
         ;
         c=getchar();
     }
     +c-',c=getchar();
     return kk*ff;
 }