动态规划——稀疏表求解RMQ问题

RMQ (Range Minimum/Maximum Query)问题，即区间最值查询问题，是求解序列中的某一段的最值的问题。如果只需要询问一次，那遍历枚举（复杂度O(n)）就是最方便且高效的方法，但如果询问次数很多（m次），O(nm)的复杂度可能就不够看了。比较容易想到的优化方法是运用预处理的思想，可以在O(n^2)的时间内预处理出所有区间的最大值，随后每一次查询都只需要O(1)的时间。这种方法在n较小但m非常大的情况下很实用，但如果n也很大的话，无论是空间还是时间都接受不了这个复杂度。

这种情况下，我们可以借助稀疏表（sparse table）和动态规划的思想，避免笨重的逐个预处理的方法：

设dp[i][j]代表从第i个元素开始，长度为2^j的区间中的最值。那么dp[i][0]就等于原序列中的第i个元素，dp[i][j]则可以由两段长度为2^(j-1)的区间合并而成。这样，就可以在o(nlogn)的时间内完成预处理。在查询时，任一区间都可以被已经预处理出来的两个区间恰好覆盖，找出这两个区间即可完成查询。预处理的时间和空间复杂度都为O(nlogn)，查询为O(1)。

下面以最大值为例，附上实现代码和需要注意的细节。

1、预处理

int n;
int a[maxn], dp[maxn][maxj];//a为原序列，元素编号为1至n
void init()//预处理
{
    for(int i = ;i <= n;i++)//初始化
    {
        for(int j = ;j < maxj;j++)
        {
            dp[i][j] = -INF;//这里可根据需要赋成其他值或是省略，此处为无穷小
        }
        dp[i][] = a[i];//dp的初始值
    }
    //因为状态转移是把两段较短的区间合并，所以要先处理出短的区间，j应在循环的外层
    for(int j = ;( << j) <= n;j++)//1 << j 运用了位运算，代表2^j
    {
        for(int i = ;( << j) + i -  <= n;i++)//dp[i][j]覆盖的区间为[i, (1 << j) + i - 1]
        {
            dp[i][j] = max(dp[i][j - ], dp[i + ( << (j - ))][j - ]);//状态转移方程，书写这里时要注意位运算符的优先级
        }
    }
}

2、查询

为了保证查询的准确性，待查区间一定要被预处理出来的区间恰好覆盖。实现这一点，只需要两段长度小于待查区间的且长度为2的幂的区间即可。例如区间[1, 5]可以用[1, 4]和[2, 5]来覆盖。

如果待查区间长度为len的话，我们只需要查询长度为2^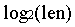的两段区间就可以了（注意log得到的结果这里向下取整了）。

int ask(int l, int r)//查询[l, r]中的最大值
{
    int len = r - l + , k = ;//len为待查区间长度
    while( << (k + ) <= len)
        k++;
    //k代表原区间可以由两段长为2^k的区间覆盖
    return max(dp[l][k], dp[r - ( << k) + ][k]);
}