[数据结构 - 第3章] 线性表之顺序表（C++实现）

一、类定义

顺序表类的定义如下：

#ifndef SEQLIST_H
#define SEQLIST_H

typedef int  ElemType; /* "ElemType类型根据实际情况而定， 这里假设为int */

class SeqList
{
public:
	SeqList(int size = 0); // 构造函数
	~SeqList(); // 析构函数

	bool isEmpty(); // 判断是否为空操作
	int getLength(); // 获取顺序表长度操作
    void clearList(); // 清空顺序表操作
	bool getElem(int i, ElemType *e); // 获取元素操作
	int locateElem(const ElemType e); // 查找元素位置操作
	bool appendList(const ElemType e); // 附加元素操作
	bool insertList(int i, const ElemType e); // 插入元素操作
	bool deleteList(int i, ElemType *e); // 删除元素操作
	void traverseList(); // 遍历顺序表

private:
	ElemType *m_pDataArr; // 指向存放顺序表元素的数组
	int m_length; // 顺序表的当前长度
	int m_maxSize; // 顺序表的最大容量
};

#endif

二、构造函数

传入用户指定的容量参数赋值给 m_maxSize，声明指针 m_pDataArr 指向 ElemType 数组，m_length 置0。

// 构造函数
SeqList::SeqList(int size)
{
	// 初始化顺序表的最大容量
	m_maxSize = size;
	// 初始化存放顺序表元素的数组
	m_pDataArr = new ElemType[m_maxSize];
	// 初始化顺序表的当前长度
	m_length = 0;
}

三、析构函数

在析构函数中释放顺序表指针申请的内存空间，并指向 NULL 避免成为野指针。

// 析构函数
SeqList::~SeqList()
{
	delete[] m_pDataArr;
	m_pDataArr = NULL;
}

四、判空和获取顺序表长度操作

m_length等于 0 则表示顺序表未空；返回 m_length 获取长度。

// 判断是否为空操作
bool SeqList::isEmpty()
{
	return m_length == 0 ? true : false;
}

// 获取顺序表长度操作
int SeqList::getLength()
{
	return m_length;
}

五、获取元素操作

先判断顺序表是否存在，且 i 是否在合理范围内；然后再将 m_pDataArr[i] 的值赋值给元素 e。

// 获取元素操作
bool SeqList::getElem(int i, ElemType *e)
{
	// 前提条件: 顺序表已存在，且i在合理范围内：0 <= i <= m_length
	if (m_length == 0 || i < 0 || i > m_length) // 若m_length==0，则说明顺序表不存在
		return false;

	*e = m_pDataArr[i];

	return true;
}

六、附加元素操作

附加元素即是在表尾后面添加元素。

// 附加元素操作
bool SeqList::appendList(const ElemType e)
{
	// 判断顺序表长度是否大于等于数组长度，是则抛出异常或动态增加容量
	if (m_length >= m_maxSize)
		return false;

	// 在表尾后面添加元素e
	m_pDataArr[m_length] = e;

	// 表长加1
	m_length++;

	return true;
}

七、插入元素操作

注意插入位置后的所有元素都要向后移动一个位置，但是在表尾下一个位置插入的这种情况，不用后移；另外允许 i 在表尾下一个位置插入。

// 插入元素操作
bool SeqList::insertList(int i, const ElemType e)
{
	// 判断顺序表是否未满 且 i是否在合法范围内
	if (m_length >= m_maxSize || i<0 || i>m_length) // 允许i在表尾下一个位置插入
		return false;

	// 从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置
	if (i <= m_length - 1) // 在表尾下一个位置插入的这种情况，不用后移
	{
		for (int k = m_length - 1; k >= i; k--)
		{
			m_pDataArr[k + 1] = m_pDataArr[k];
		}
	}

	// 将要插入元素填入位置i处
	m_pDataArr[i] = e;
	// 表长+1
	m_length++;

	return true;
}

八、删除元素操作

注意若删除位置在表尾，则不需要前移。

// 删除元素操作
bool SeqList::deleteList(int i, ElemType *e)
{
	// 判断顺序表是否未满 且 i是否在合法范围内
	if (m_length == 0 || i<0 || i>m_length - 1)
		return false;

	// 取出删除元素
	*e = m_pDataArr[i];

	// 从删除元素的下一个位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置
	if (i != m_length - 1) // 【若删除位置在表尾，则不需要前移】
	{
		// 将删除元素的下一个位置及后面元素向前移动一位
		for (int k = i; k < m_length - 1; k++)
			m_pDataArr[k] = m_pDataArr[k + 1];
	}

	// 表长减1
	m_length--;

	return true;
}

九、遍历操作

遍历前需要判断顺序表是否存在，以及是否为空表

// 遍历顺序表
void SeqList::traverseList()
{
	// 判断顺序表是否存在，以及是否为空表
	if (m_pDataArr == NULL || m_length == 0)
		return;

	for (int i = 0; i < m_length; i++)
	{
		cout << m_pDataArr[i] << " ";
	}
	cout << endl;
}

十、主函数执行

在主函数中执行的代码如下：

#include "stdafx.h"
#include <stdlib.h>
#include <iostream>
#include "seqListCpp.h"

using namespace std;

int main()
{
	// 初始化顺序表
	SeqList seqList(20);

	// 附加元素0-2到顺序表
	cout << "附加元素0-2到顺序表!" << endl;
	for (int i = 0; i<3; i++)
	{
		seqList.appendList(i);
	}
	cout << endl;

	// 在位置2插入元素到9顺序表
	cout << "在位置2插入元素9到顺序表!" << endl << endl;
	seqList.insertList(2, 9);

	// 在位置3删除元素
	int value1;
	if (seqList.deleteList(3, &value1) == false)
	{
		cout << "delete error!" << endl;
		return -1;
	}
	else
	{
		cout << "在位置3删除元素，删除的元素为：" << value1 << endl << endl;
	}

	// 查找元素位置
	int index = seqList.locateElem(0);
	if (index == -1)
	{
		cout << "locate error!" << endl;
		return -1;
	}
	else
	{
		cout << "查找到元素0的位置为：" << index << endl << endl;
	}

	// 遍历顺序表
	cout << "遍历顺序表： ";
	seqList.traverseList();
	cout << endl;

	// 清空顺序表
	cout << "清空顺序表!" << endl << endl;
	seqList.clearList();

	return 0;
}

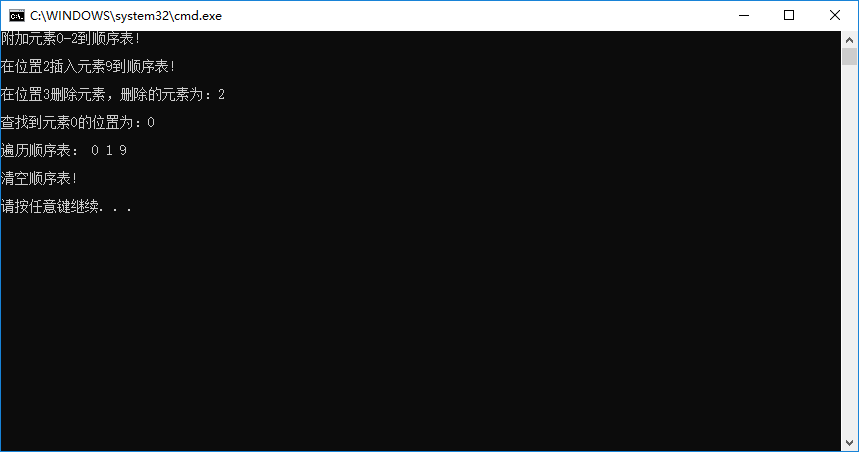
输出结果如下图所示（编译器为VS2013）：