JSOI 2010 连通数

洛谷 P4306 [JSOI2010]连通数

洛谷传送门

题目描述

度量一个有向图联通情况的一个指标是连通数，指图中可达顶点对个的个数。

如图

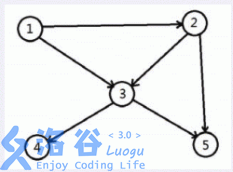
顶点 11 可达 1,_2,3,_4,51, 2, 3, 4, 5

顶点 22 可达 2,_3,4,~52, 3, 4, 5

顶点 33 可达 3,_4,53, 4, 5

顶点 4,~54, 5 都只能到达自身。

所以这张图的连通数为 1414。

给定一张图，请你求出它的连通数

输入格式

输入数据第一行是图顶点的数量，一个正整数N。 接下来N行，每行N个字符。第i行第j列的1表示顶点i到j有边，0则表示无边。

输出格式

输出一行一个整数，表示该图的连通数。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

对于100%的数据，N不超过2000。

题解：

好不容易碰上一道紫水题

人生中首次自己自主AC紫题，感觉比我国爆破第一颗原子弹还激动...

大家都使用的tarjan缩点、反向建图等正解做法，但是这些复杂图论我不是很会。

我一开始想到的是SPFA，我每个点跑一遍最短路，跑完之后开始从1到n扫，如果dist数组被更新了就说明此点可达，累加ans。

最后直接输出即可

数据还是比较水的，请求洛谷加强数据，我这个算法的时间复杂度奇高，预期TLE5个点，但是竟然AC了...

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int n,ans;
char s[2010];
int tot,to[4000001],nxt[4000001],head[2001];
int dist[2001],v[2001];
void add(int x,int y)
{
    to[++tot]=y;
    nxt[tot]=head[x];
    head[x]=tot;
}
void spfa(int start)
{
    for(int i=1;i<=n;i++)
        dist[i]=1e9,v[i]=0;
    queue<int> q;
    q.push(start);
    v[start]=1;
    dist[start]=0;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        v[x]=0;
        for(int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(dist[y]>dist[x]+1)
            {
                dist[y]=dist[x]+1;
                if(v[y]==0)
                    q.push(y),v[y]=1;
            }
        }
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s+1);
        for(int j=1;j<=n;j++)
            if(s[j]=='1')
                add(i,j);
    }
    for(int i=1;i<=n;i++)
    {
        spfa(i);
        for(int j=1;j<=n;j++)
            if(dist[j]<1e9)
                ans++;
    }
    printf("%d",ans);
    return 0;
}