雅克比(Jacobi)方法

可以用来求解协方差矩阵的特征值和特征向量。

雅可比方法(Jacobian method)求全积分的一种方法，把拉格朗阶查皮特方法推广到求n个自变量一阶非线性方程的全积分的方法称为雅可比方法。

雅克比迭代法的计算公式简单，每迭代一次只需计算一次矩阵和向量的乘法，且计算过程中原始矩阵A始终不变，比较容易并行计算。

考虑线性方程组Ax=b时，一般当A为低阶稠密矩阵时，用主元消去法解此方程组是有效方法。但是，对于由工程技术中产生的大型稀疏矩阵方程组（A的阶数很高，但零元素较多，例如求某些偏微分方程数值解所产生的线性方程组），利用迭代法求解此方程组就是合适的，在计算机内存和运算两方面，迭代法通常都可利用A中有大量零元素的特点。雅克比迭代法就是众多迭代法中比较早且较简单的一种，其命名也是为纪念普鲁士著名数学家雅可比。

原理

【收敛性】设Ax=b，其中A=D+L+U为非奇异矩阵，且对角阵D也非奇异，则当迭代矩阵J的谱半径ρ（J）<1时，雅克比迭代法收敛。

首先将方程组中的系数矩阵A分解成三部分，即：A = L+D+U，其中D为对角阵，L为下三角矩阵，U为上三角矩阵。

• 之后确定迭代格式，X^(k+1) = B*X^(k) +f ，（这里^表示的是上标，括号内数字即迭代次数），其中B称为迭代矩阵，雅克比迭代法中一般记为J。（k = 0,1，......）
• 再选取初始迭代向量X^(0)，开始逐次迭代。

            

【优缺点】雅克比迭代法的优点明显，计算公式简单，每迭代一次只需计算一次矩阵和向量的乘法，且计算过程中原始矩阵A始终不变，比较容易并行计算。然而这种迭代方式收敛速度较慢，而且占据的存储空间较大，所以工程中一般不直接用雅克比迭代法，而用其改进方法。

实现

通过雅克比(Jacobi)方法求实对称矩阵的特征值和特征向量操作步骤：S′=G^TSG,其中G是旋转矩阵，S′和S均为实对称矩阵，S′和S有相同的Frobenius norm，可以用一个最简单的3维实对称矩阵为例，根据公式进行详细推导(参考 维基百科 )：

通过旋转矩阵将对称矩阵转换为近似对角矩阵，进而求出特征值和特征向量，对角矩阵中主对角元素即为S近似的实特征值。Jacobi是通过迭代方法计算实对称矩阵的特征值和特征向量。

• (1)、初始化特征向量V为单位矩阵；
• (2)、初始化特征值eigenvalues为矩阵S主对角线元素；
• (3)、将二维矩阵S赋值给一维向量A；
• (4)、查找矩阵S中，每行除主对角元素外(仅上三角部分)绝对值最大的元素的索引赋给indR；
• (5)、查找矩阵S中，第k列，前k个元素中绝对值最大的元素的索引赋给indC；
• (6)、查找pivot的索引(k, l)，并获取向量A中绝对值最大的元素p；
• (7)、如果p的绝对值小于设定的阈值则退出循环；
• (8)、计算sinθ(s)和cosθ(c)的值；
• (9)、更新(k, l)对应的A和eigenvalues的值；
• (10)、旋转A的(k，l)；
• (11)、旋转特征向量V的(k,l)；
• (12)、重新计算indR和indC；
• (13)、循环执行以上(6)~(12)步，直到达到最大迭代次数，OpenCV中设置迭代次数为n*n*30；
• (14)、如果需要对特征向量和特性值进行sort，则执行sort操作。

相关概念

旋转

旋转矩阵性质：设M是任何维的一般旋转矩阵：M∈R^n*n

• (1)、两个向量的点积(内积)在它们都被一个旋转矩阵操作之后保持不变：a·b=Ma·Mb；
• (2)、从而得出旋转矩阵的逆矩阵是它的转置矩阵：MM^-1=MM^T=I 这里的I是单位矩阵；
• (3)、一个矩阵是旋转矩阵，当且仅当它是正交矩阵并且它的行列式是单位一。正交矩阵的行列式是±1；则它包含了一个反射而不是真旋转矩阵；
• (4)、旋转矩阵是正交矩阵，如果它的列向量形成Rⁿ的一个正交基，就是说在任何两个列向量之间的标量积是零(正交性)而每个列向量的大小是单位一(单位向量)。

在二维空间中，旋转可以用一个单一的角θ定义。作为约定，正角表示逆时针旋转。把笛卡尔坐标的列向量关于原点逆时针旋转θ的矩阵是：

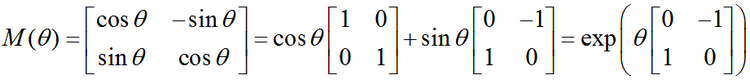
对角矩阵

对角矩阵(diagonal matrix)：只在主对角线上含有非零元素，其它位置都是零，对角线上的元素可以为0或其它值。形式上，矩阵D是对角矩阵，当且仅当对于所有的i≠j, D_i,j= 0. 单位矩阵就是对角矩阵，对角元素全部是1。

用diag(v)表示一个对角元素由向量v中元素给定的对角方阵。

对角矩阵的乘法计算很高效。计算乘法diag(v)x，我们只需要将x中的每个元素xi放大vi倍。换言之，diag(v)x = v⊙x。

计算对角方阵的逆矩阵也很高效。对角方阵的逆矩阵存在，当且仅当对角元素都是非零值，在这种情况下，diag(v)-1=diag([1/v1, …, 1/vn]T)。

通过将一些矩阵限制为对角矩阵，我们可以得到计算代价较低的(并且简明扼要的)算法。

特征分解

特征分解：线性代数中，特征分解(Eigende composition)，又称谱分解(Spectral decomposition)是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。

需要注意只有对可对角化矩阵(如果一个方块矩阵A相似于对角矩阵，也就是说，如果存在一个可逆矩阵P使得P^-1AP是对角矩阵，则它就被称为可对角化的)才可以施以特征分解。

特征分解(eigen decomposition)是使用最广的矩阵分解之一，即我们将矩阵分解成一组特征向量和特征值。

方阵A的特征向量(eigen vector)是指与A相乘后相当于对该向量进行缩放的非零向量v：Av=λv。标量λ被称为这个特征向量对应的特征值(eigenvalue)。(类似地，我们也可以定义左特征向量(left eigen vector) v^TA=λV^T，但是通常我们更关注右特征向量(right eigen vector))。 如果v是A的特征向量，那么任何缩放后的向量sv(s∈R,s≠0)也是A的特征向量。此外，sv和v有相同的特征值。基于这个原因，通常我们只考虑单位特征向量。

假设矩阵A有n个线性无关的特征向量{v(1),…,v(n)}，对应着特征值{λ1,…,λn}。我们将特征向量连接成一个矩阵，使得每一列是一个特征向量：V=[v(1),…,v(n)]。类似地，我们也可以将特征值连接成一个向量λ=[λ1,…,λn]^T。因此A的特征分解(eigen decomposition)可以记作：A=Vdiag(λ)V^-1。

在某些情况下，特征分解存在，但是会涉及到复数，而非实数。每个实对称矩阵都可以分解成实特征向量和实特征值：A=QΛQ^T。其中Q是A的特征向量组成的正交矩阵，Λ是对角矩阵。特征值Λ_i,i对应的特征向量是矩阵Q的第i列，记作Q_:,i。因为Q是正交矩阵，我们可以将A看作是沿方向v(i)延展λi倍的空间。

虽然任意一个实对称矩阵A都有特征分解，但是特征分解可能并不唯一。如果两个或多个特征向量拥有相同的特征值，那么在由这些特征向量产生的生成子空间中，任意一组正交向量都是该特征值对应的特征向量。

所有特征值都是正数的矩阵被称为正定(positive definite)；所有特征值都是非负数的矩阵被称为半正定(positive semidefinite)。同样地，所有特征值都是负数的矩阵被称为负定(negative definite)；所有特征值都是非正数的矩阵被称为半负定(negative semidefinite)。半正定矩阵受到关注是因为它们保证Ⅴx,x^TAx≥0。此外，正定矩阵还保证x^TAx=0 =>x=0。

参考

https://en.wikipedia.org/wiki/Jacobi_eigenvalue_algorithm

https://blog.csdn.net/fengbingchun/article/details/72801310?utm_source=blogxgwz0