二叉树 B-树B+树

聚集索引和非聚集索引结构参考：http://blog.csdn.net/cangchen/article/details/44818623

前两天有位朋友邀请我回答个问题，为什么 MongoDB （索引）使用B-树而 Mysql 使用 B+树？我觉得这个问题非常好，从实际应用的角度来学习数据结构，没有比这更好的方法了。因为像 Mysql 和 MongoDB 这种经久考验的大型软件在设计上都是精益求精的，它们为什么选择这些数据结构？:)

本文从实际应用的角度来介绍以及分析B-树和B+树。

B-树由来

定义：B-树是一类树，包括B-树、B+树、B*树等，是一棵自平衡的搜索树，它类似普通的平衡二叉树，不同的一点是B-树允许每个节点有更多的子节点。B-树是专门为外部存储器设计的，如磁盘，它对于读取和写入大块数据有良好的性能，所以一般被用在文件系统及数据库中。

定义只需要知道B-树允许每个节点有更多的子节点即可。子节点数量一般在上千，具体数量依赖外部存储器的特性。

先来看看为什么会出现B-树这类数据结构。

传统用来搜索的平衡二叉树有很多，如 AVL 树，红黑树等。这些树在一般情况下查询性能非常好，但当数据非常大的时候它们就无能为力了。原因当数据量非常大时，内存不够用，大部分数据只能存放在磁盘上，只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns，而磁盘在 10 ms 左右。速度相差了近 5 个数量级，磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能？减少磁盘 IO 次数，像 AVL 树，红黑树这类平衡二叉树从设计上无法“迎合”磁盘。

上图是一颗简单的平衡二叉树，平衡二叉树是通过旋转来保持平衡的，而旋转是对整棵树的操作，若部分加载到内存中则无法完成旋转操作。其次平衡二叉树的高度相对较大为 log n（底数为2），这样逻辑上很近的节点实际可能非常远，无法很好的利用磁盘预读（局部性原理），所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。

空间局部性原理：如果一个存储器的某个位置被访问，那么将它附近的位置也会被访问。

我们从“迎合”磁盘的角度来看看B-树的设计。

索引的效率依赖与磁盘 IO 的次数，快速索引需要有效的减少磁盘 IO 次数，如何快速索引呢？索引的原理其实是不断的缩小查找范围，就如我们平时用字典查单词一样，先找首字母缩小范围，再第二个字母等等。平衡二叉树是每次将范围分割为两个区间。为了更快，B-树每次将范围分割为多个区间，区间越多，定位数据越快越精确。那么如果节点为区间范围，每个节点就较大了。所以新建节点时，直接申请页大小的空间（磁盘是按 block 分的，一般为 512 Byte。磁盘 IO 一次读取若干个 block，我们称为一页，具体大小和操作系统有关，一般为 4 k，8 k或 16 k），计算机内存分配是按页对齐的，这样就实现了一个节点只需要一次 IO。

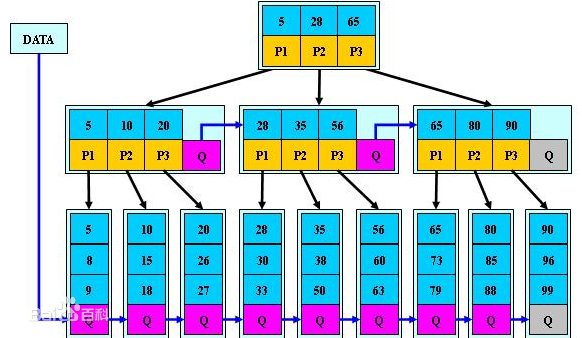
上图是一棵简化的B-树，多叉的好处非常明显，有效的降低了B-树的高度，为底数很大的 log n，底数大小与节点的子节点数目有关，一般一棵B-树的高度在 3 层左右。层数低，每个节点区确定的范围更精确，范围缩小的速度越快。上面说了一个节点需要进行一次 IO，那么总 IO 的次数就缩减为了 log n 次。B-树的每个节点是 n 个有序的序列(a1,a2,a3…an)，并将该节点的子节点分割成 n+1 个区间来进行索引(X1< a1, a2 < X2 < a3, … , an+1 < Xn < anXn+1 > an)。

B-树

上图是一颗B-树，B-树的每个节点有 d~2d 个 key，2 这个因子指明了树的分裂及合并的规则，这个规则维持了B-树的平衡。

B-树的插入和删除就不具体介绍了，很多资料都描述了这一过程。在普通平衡二叉树中，插入删除后若不满足平衡条件则进行旋转操作，而在B-树中，插入删除后不满足条件则进行分裂及合并操作。

简单叙述下分裂及合并操作。

分裂：如果有一个节点有 2d 个 key，增加一个后为 2d+1 个 key，不符合上述规则 B-树的每个节点有 d~2d 个 key，大于 2d，则将该节点进行分裂，分裂为两个 d 个 key 的节点并将中值 key 归还给父节点。
合并：如果有一个节点有 d 个 key，删除一个后为 d-1 个 key，不符合上述规则 B-树的每个节点有 d~2d 个 key，小于 d，则将该节点进行合并，合并后若满足条件则合并完成，不满足则均分为两个节点。

B-树的查找

我们来看看B-树的查找，假设每个节点有 n 个 key值，被分割为 n+1 个区间，注意，每个 key 值紧跟着 data 域，这说明B-树的 key 和 data 是聚合在一起的。一般而言，根节点都在内存中，B-树以每个节点为一次磁盘 IO，比如上图中，若搜索 key 为 25 节点的 data，首先在根节点进行二分查找（因为 keys 有序，二分最快），判断 key 25 小于 key 50，所以定位到最左侧的节点，此时进行一次磁盘 IO，将该节点从磁盘读入内存，接着继续进行上述过程，直到找到该 key 为止。

查找伪代码

Data* BTreeSearch(Root *node, Key key)

{

    Data* data;

    if(root == NULL)

        return NULL;

    data = BinarySearch(node);

    if(data->key == key)

    {

        return data;

    }else{

        node = ReadDisk(data->next);

        BTreeSearch(node, key);

    }

}

B+树

B+树是B-树的变种，它与B-树的不同之处在于：

在B+树中，key 的副本存储在内部节点，真正的 key 和 data 存储在叶子节点上。
n 个 key 值的节点指针域为 n 而不是 n+1。

如下图为一颗B+树：

因为内节点并不存储 data，所以一般B+树的叶节点和内节点大小不同，而B-树的每个节点大小一般是相同的，为一页。

为了增加区间访问性，一般会对B+树做一些优化。
如下图带顺序访问的B+树。

B*树：在B+树基础上，为非叶子结点也增加链表指针

B-树和B+树的区别

1.B+树内节点不存储数据，所有 data 存储在叶节点导致查询时间复杂度固定为 log n。而B-树查询时间复杂度不固定，与 key 在树中的位置有关，最好为O(1)。

如下所示B-树/B+树查询节点 key 为 50 的 data。

B-树

从上图可以看出，key 为 50 的节点就在第一层，B-树只需要一次磁盘 IO 即可完成查找。所以说B-树的查询最好时间复杂度是 O(1)。

B+树

由于B+树所有的 data 域都在根节点，所以查询 key 为 50的节点必须从根节点索引到叶节点，时间复杂度固定为 O(log n)。

2.B+树叶节点两两相连可大大增加区间访问性，可使用在范围查询等，而B-树每个节点 key 和 data 在一起，则无法区间查找。

根据空间局部性原理：如果一个存储器的某个位置被访问，那么将它附近的位置也会被访问。

B+树可以很好的利用局部性原理，若我们访问节点 key为 50，则 key 为 55、60、62 的节点将来也可能被访问，我们可以利用磁盘预读原理提前将这些数据读入内存，减少了磁盘 IO 的次数。
当然B+树也能够很好的完成范围查询。比如查询 key 值在 50-70 之间的节点。

3.B+树更适合外部存储。由于内节点无 data 域，每个节点能索引的范围更大更精确

这个很好理解，由于B-树节点内部每个 key 都带着 data 域，而B+树节点只存储 key 的副本，真实的 key 和 data 域都在叶子节点存储。前面说过磁盘是分 block 的，一次磁盘 IO 会读取若干个 block，具体和操作系统有关，那么由于磁盘 IO 数据大小是固定的，在一次 IO 中，单个元素越小，量就越大。这就意味着B+树单次磁盘 IO 的信息量大于B-树，从这点来看B+树相对B-树磁盘 IO 次数少。

从上图可以看出相同大小的区域，B-树仅有 2 个 key，而B+树有 3 个 key。

为什么 MongoDB 索引选择B-树，而 Mysql 索引选择B+树

这些内容了解后，我们来看为什么 MongoDB 索引选择B-树，而 Mysql （InooDB 引擎）索引选择B+树。

Mysql 大家应该比较熟悉，传统的关系型数据库，下面介绍下 MongoDB。

来看下 wiki 百科上 MongoDB 的定义：

MongoDB (from humongous) is a cross-platform document-oriented database. Classified as a NoSQL database, MongoDB eschews the traditional table-based relational database structure in favor of JSON-like documents with dynamic schemas (MongoDB calls the format BSON)

这段话的大致意思是 MongoDB 是文档型的数据库，是一种 nosql，它使用类 Json 格式保存数据。

文档型数据库和我们常见的关系型数据库不同，一般使用 XML 或 Json 格式来保存数据，归属于聚合型数据库。

键值数据库也属于聚合型数据库，熟悉 Redis 的同学应该很好理解。

举个例子：

加入我们要建立一个电子商务网站，类似淘宝这种将商品销售给用户，那么必须存储用户信息、商品目录、订单、收货地址、账单地址、付款方式等。

看下传统的关系型数据库是如何存储的：

聚合型数据库存储模型：

用类似 Json 的格式表示如下：

//Customer

{

        "id":1,

        "name":Tom,

        "billingAddress":[{"city":"China"}]

}

//Orders

{

        "id":99,

        "orderItem":[

                "productId"27,

                "price":100,

                "productName":book

         ],

         "shippingAddress":[{"city":"china"}],

         "orderPayment":[

            ...

        ]

}

相对于 Mysql 关系型数据库，MongoDB 这类 nosql 适用于数据模型简单，性能要求高的场合

为什么 MongoDB 使用B-树

MongoDB 是一种 nosql，也存储在磁盘上，被设计用在数据模型简单，性能要求高的场合。性能要求高，看看B/B+树的区别第一点：

B+树内节点不存储数据，所有 data 存储在叶节点导致查询时间复杂度固定为 log n。而B-树查询时间复杂度不固定，与 key 在树中的位置有关，最好为O(1)

我们说过，尽可能少的磁盘 IO 是提高性能的有效手段。MongoDB 是聚合型数据库，而 B-树恰好 key 和 data 域聚合在一起。

为什么 Mysql 使用B+树

Mysql 是一种关系型数据库，区间访问是常见的一种情况，而 B-树并不支持区间访问（可参见上图），而B+树由于数据全部存储在叶子节点，并且通过指针串在一起，这样就很容易的进行区间遍历甚至全部遍历。见B/B+树的区别第二点：

B+树叶节点两两相连可大大增加区间访问性，可使用在范围查询等，而B-树每个节点 key 和 data 在一起，则无法区间查找。

其次B+树的查询效率更加稳定，数据全部存储在叶子节点，查询时间复杂度固定为 O(log n)。

最后第三点：

B+树更适合外部存储。由于内节点无 data 域，每个节点能索引的范围更大更精确