【转载】 KL距离（相对熵）

原文地址：

https://www.cnblogs.com/nlpowen/p/3620470.html

-----------------------------------------------------------------------------------------------

KL距离，是Kullback-Leibler差异（Kullback-Leibler Divergence）的简称，也叫做相对熵（Relative Entropy）。它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布P(x)对应的每个事件，若用概率分布 Q(x)编码时，平均每个基本事件（符号）编码长度增加了多少比特。我们用D（P||Q）表示KL距离，计算公式如下：

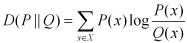
当两个概率分布完全相同时，即P(X)=Q(X)，其相对熵为0 。我们知道，概率分布P(X)的信息熵为：

其表示，概率分布P(x)编码时，平均每个基本事件（符号）至少需要多少比特编码。通过信息熵的学习，我们知道不存在其他比按照本身概率分布更好的编码方式了，所以D(P||Q）始终大于等于0的。虽然KL被称为距离，但是其不满足距离定义的三个条件：1）非负性（满足）；2）对称性（不满足）；3）三角不等式 （不满足）。

我们以一个例子来说明，KL距离的含义。

假如一个字符发射器，随机发出0和1两种字符，真实发出概率分布为A，但实际不知道A的具体分布。现在通过观察，得到概率分布B与C。各个分布的具体情况如下：

A(0)=1/2，A(1)=1/2

B(0)=1/4，B(1)=3/4

C(0)=1/8，C(1)=7/8

那么，我们可以计算出得到如下：

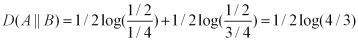
也即，这两种方式来进行编码，其结果都使得平均编码长度增加了。我们也可以看出，按照概率分布B进行编码，要比按照C进行编码，平均每个符号增加的比特数目少。从分布上也可以看出，实际上B要比C更接近实际分布（因为其与A分布的KL距离更近）。

如果实际分布为C，而我们用A分布来编码这个字符发射器的每个字符，那么同样我们可以得到如下：

再次，我们进一步验证了这样的结论：对一个信息源编码，按照其本身的概率分布进行编码，每个字符的平均比特数目最少。这就是信息熵的概念，衡量了信息源本身的不确定性。另外，可以看出KL距离不满足对称性，即D(P||Q)不一定等于D(Q||P)。

当然，我们也可以验证KL距离不满足三角不等式条件。

上面的三个概率分布，D(B||C)=1/4log2+3/4log(6/7)。可以得到：D(A||C) - (D(A||B)+ D(B||C)) =1/2log2+1/4log(7/6)>0，这里验证了KL距离不满足三角不等式条件。所以KL距离，并不是一种距离度量方式，虽然它有这样的学名。

其实，KL距离在信息检索领域，以及统计自然语言方面有重要的运用。

-----------------------------------------------------------------------------------------------