ZROI 暑期高端峰会 A班 Day1 组合计数

AGC036F Square Constriants

一定有 \(l_i<p_i\le r_i\)。

考虑朴素容斥，枚举每个数是 \(\le l_i\) 还是 \(\le r_i\)。对于 \(p_i\le x_i\)，方案数是：把 \(x\) 排序后 \(\prod(x_i+1-i)\)（下标从 \(0\) 开始）。

太慢了。

把 \(l_0\) 到 \(l_{n-1}\)，\(r_0\) 到 \(r_{2n-1}\) 一起排序。（\(l_n\) 到 \(l_{2n-1}\) 不用管，他们非正）

把 \(l_0\) 到 \(l_{n-1}\) 叫 A 类数。

把 \(r_n\) 到 \(r_{2n-1}\) 叫 B 类数。

把 \(r_0\) 到 \(r_{n-1}\) 叫 C 类数。

那么排序后一定形如 ABBAABABABACCCCCCC...。

所有 B 都要选， 每对 AC 中选一个。

先枚举一共选了多少个 A（设为 \(k\)）

\(f[i][j]\) 表示前 \(i\) 个数中选了 \(j\) 个 A。对每次枚举进行 DP。

时间复杂度 \(O(n^3)\)。

LNR R2 D1 T3 不等关系

把大于号变成（没有限制-小于号）。

考虑朴素容斥，对于只有小于号和没有限制的方案数是 \(\frac{(n+1)!}{\prod(p_i+1)!}\)，\(p_i\) 是每段连续的小于号的长度。

太慢了。

\(f[i]\) 表示将前 \(i\) 个数分完段了。答案是 \(f[n](n+1)!\)。

枚举上一个选没有限制的位置 \(j\)，\(f[i]=\sum f[j]\frac{1}{(i-j)!}(-1)^{s_i-s_j}\)，\(s_i\) 表示前缀中大于号的个数。

可以分治 FFT 优化到 \(O(n\log^2n)\)，多项式求逆优化到 \(O(n\log n)\)。

AGC035F Two Histograms

掉线……

CTS 2019 D1T1 随机立方体

求概率和求方案数没什么区别。

三维比较复杂，先考虑二维，是类似的。

二项式反演，计算至少 \(k\) 个极大的数的方案数会更好做。

首先每行每列都至多只有一个数是极大的。

不妨把这 \(k\) 个极大的数放到主对角线的左上，这样好考虑。只要保证这 \(k\) 个极大，剩下的都随便放。

同时，这 \(k\) 个极大的数从左上到右下是递减的。

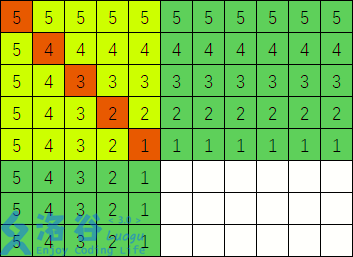
比如上图这样。（图片来源：兔队）

选出这 \(k\) 个极大数有 \(n^\underline{k}m^\underline{k}\) 种选择（要考虑顺序，也就是大小关系）。

对于红色部分，每个点都要小于左上的点。

对于黄绿色部分，每个点都要小于和它同一行和同一列的红点。由于红点已经有大小关系，所以让主对角线左下的点小于它右面的红点，右上的点小于它下面的红点就行了。

对于绿色部分，也是小于与它同一行或者同一列的红点。

对于白色部分，没有限制。

把大小关系连成一个森林。

有结论：给一个 \(n\) 个点的有根树森林赋点权，赋成 \(1\) 到 \(n\) 的排列，那么这棵森林中都是“堆”的方案数是 \(\frac{n!}{\prod size_u}\)。应该很好理解，从浅往深考虑，把最大的要放到这棵子树的根处，在 \(size_u!\) 种方案中有 \((size_u-1)!\) 种。

所以这里的方案数就是 \(\frac{(nm)!}{\prod\limits_{i=1}^k(nm-(n-i)(m-i))}\)。

三维也差不多。所以至少 \(k\) 个极大点的方案数是 \(n^\underline{k}m^\underline{k}l^\underline{k}\frac{(nml)!}{\prod\limits_{i=1}^k(nml-(n-i)(m-i)(l-i))}\)。由于要求期望，把分子上的 \((nml)!\) 丢掉就行了。

二项式反演一波走人。时间复杂度可以做到 \(O(\min(n,m,l))\)。

Endless Spin

长度为 \(n\) 的区间，每次随机一段染黑，问期望多少次全部染黑。

\(n\le 100\)

直接 min-max 容斥。

\[E(\max t_i)=\sum\limits_{S\subseteq U}(-1)^{|S|+1}E(\min\limits_{i\in S} t_i)\]

染不到第 \(i\) 块的概率是 \(\frac{i(i+1)+(n-i+1)(n-i+2)}{n(n+1)}\)。

\(f[i][j][k]\) 表示考虑前 \(i\) 个位置，当前最后一段区间长 \(k\)，总的选法（上面的分子）为 \(j\)。

如果下一个不选，可以转移到 \(f[i+1][j+k+1][k+1]\)。

如果下一个选，可以转移到 \(f[i+1][j][0]\)。（要先乘上系数 \(-1\)）

答案是 \(\sum\limits_{j=0}^{\binom{n+1}{2}-1}\frac{f[n][j][k]}{1-\frac{j}{\binom{n+1}{2}}}\)。

（还是不懂……）

Random Graph

给 \(n\) 个点的图，一开始没有边，每次随机两个点，然后连边。可能会随机到自环和重边。

问期望多长时间联通。

\(n\le 100\)

\(n\) 个点 \(m\) 条边的连通图个数怎么算？

考虑求不连通的图个数，枚举 \(1\) 所在的连通块的点数和边数。

\[f[n][m]=\binom{\binom{n}{2}}{m}-\sum\limits_{i=1}^{n-1}\sum\limits_{j=0}^m\binom{n-1}{i-1}f[i][j]\binom{\binom{n-i}{2}}{m-j}\]

概率呢？\(n\) 个点 \(m\) 条边的连通概率。

\[g[n][m]=1-\sum\limits_{i=1}^{n-1}\sum\limits_{j=0}^m\binom{n-1}{i-1}\binom{m}{j}(\frac{i^2}{n^2})^j(\frac{(n-i)^2}{n^2})^{m-j}g[i][j]\]

令 \(h[n][m]=1-g[n][m]\)，也就是不连通概率。

答案就是 \(\sum h[n][m]\)。

下证 \(g[n][m]\) 可以表示成 \(\sum\limits_{i=0}^{n^2}C_{n,i}(\frac{i}{n^2})^m\)。其中 \(C_{n,i}\) 是某些常数。

证明不难。并且可以证明 \(C_{n,n^2}=1\)。

那么答案是 \(\sum\limits_{m\ge 0}(-\sum\limits_{i=0}^{n^2-1}C_{n,i}(\frac{i}{n^2})^m)=\sum\limits_{i=0}^{2n-1}-C_{n,i}\sum\limits_{m\ge 0}(\frac{i}{n^2})^m\)。

怎么求 \(C_{n,i}\)？

掉线了，以后再说。

LGV 引理

在一个 DAG 上，如果有一些起点 \(a_i\)，一些终点 \(b_i\)，如果在 \(a_i\rightarrow b_j,a_k\rightarrow b_l\) 相交时必有 \(i<k,j>l\)，那么不相交的路径条数为 \(\det(g(i,j))\)，\(g(i,j)\) 表示 \(a_i\) 到 \(b_j\) 的路径条数。

某经典题

\(n\times m\) 的矩阵中，填 \(1\) 到 \(k\)，要求每个数都要 \(\ge\) 右边的数和下面的数，问多少种方案。

考虑画出每种数的轮廓线。这些轮廓线必不相交（可能部分或全部重合）。

反过来，没有交点的轮廓线一定可以对应一种矩阵。

LGV 引理一下即可。

EI 与菱形计数

想象成是一个立体图，\(a\times b\) 的矩阵，每个上面可以堆立方体，至多 \(c\) 个。

然后就变成上面的经典题了。

那个行列式也可以推出来是个很简洁的东西。

（具体去讨论看吧）