【PyTorch v1.1.0文档研习】60分钟快速上手

阅读文档：使用 PyTorch 进行深度学习：60分钟快速入门。

本教程的目标是：

• 总体上理解 PyTorch 的张量库和神经网络
• 训练一个小的神经网络来进行图像分类

PyTorch 是个啥？

这是基于 Python 的科学计算包，其目标是：

• 替换 NumPy，发挥 GPU 的作用
• 一个提供最大灵活性和速度的深度学习研究平台

起步

PyTorch 中的 Tensor 类似于 NumPy 中的 ndarray（这一点类似于 TensorFlow），只不过张量可以充分利用 GPU 来进行加速计算。

 from __future__ import print_function
 import torch

构建一个 5*3 的矩阵：

 x = torch.empty(5, 3)
 print(x)

tensor([[7.0976e+22, 1.8515e+28, 4.1988e+07],
        [3.0357e+32, 2.7224e+20, 7.7782e+31],
        [4.7429e+30, 1.3818e+31, 1.7225e+22],
        [1.4602e-19, 1.8617e+25, 1.1835e+22],
        [4.3066e+21, 6.3828e+28, 1.4603e-19]])

直接通过数据来构建张量：

 x = torch.tensor([5.5, 3])
 print(x)

tensor([5.5000, 3.0000])

还可以根据已有张量来创建张量。这个方法会重用输入张量的属性（例如 dtype）。

 x = x.new_ones(5, 3, dtype=torch.double)  # new_* methods take in sizes
 print(x)

 x = torch.randn_like(x, dtype=torch.float)  # override dtype!
 print(x)                                    # result has the same size

tensor([[., ., .],
        [., ., .],
        [., ., .],
        [., ., .],
        [., ., .]], dtype=torch.float64)
tensor([[ 0.4845, -1.2227, -1.2535],
        [ 0.2278,  0.9922,  0.5871],
        [-1.8249,  0.6308,  1.0100],
        [ 0.0126,  0.0591, -0.6153],
        [ 0.1847, -1.8002,  0.7629]])

获取张量的大小：

 print(x.size())

torch.Size([, ])

注意：torch.Size 对象实际上是元组，支持所有元组操作。

运算

PyTorch 支持多种运算语法（类似于 TensorFlow），下面我们看看各种加法的运算。

加法语法 1：

 y = torch.rand(5, 3)
 print(x + y)

tensor([[ 1.2256, -0.4395, -0.4990],
        [ 0.4846,  1.7138,  1.0470],
        [-1.3466,  0.7643,  1.0811],
        [ 0.4865,  0.7320, -0.4655],
        [ 0.5111, -1.0667,  1.2088]])

加法语法 2：

 print(torch.add(x, y))

tensor([[ 1.2256, -0.4395, -0.4990],
        [ 0.4846,  1.7138,  1.0470],
        [-1.3466,  0.7643,  1.0811],
        [ 0.4865,  0.7320, -0.4655],
        [ 0.5111, -1.0667,  1.2088]])

输出张量作为参数的加法：

 result = torch.empty(5, 3)
 torch.add(x, y, out=result)
 print(result)

tensor([[ 1.2256, -0.4395, -0.4990],
        [ 0.4846,  1.7138,  1.0470],
        [-1.3466,  0.7643,  1.0811],
        [ 0.4865,  0.7320, -0.4655],
        [ 0.5111, -1.0667,  1.2088]])

就地（in-place）的加法：

 y.add_(x)
 print(y)

tensor([[ 1.2256, -0.4395, -0.4990],
        [ 0.4846,  1.7138,  1.0470],
        [-1.3466,  0.7643,  1.0811],
        [ 0.4865,  0.7320, -0.4655],
        [ 0.5111, -1.0667,  1.2088]])

注意：所有让张量就地发生变化的运算都会在后面加上 _（例如：x.copy_(y)、x.t_()）。

随时可以使用类似于 Numpy 的索引操作。

 print(x[:, 1])

tensor([-1.2227,  0.9922,  0.6308,  0.0591, -1.8002])

如果需要改变张量的形状，使用 torch.view：

 x = torch.randn(4, 4)
 y = x.view(16)
 z = x.view(-1, 8)  # -1 所在的维度通过推断得出
 print(x.size(), y.size(), z.size())

torch.Size([, ]) torch.Size([]) torch.Size([, ])

如果张量只有一个元素，可以通过 .item() 直接获取 Python 数值。

 x = torch.randn(1)
 print(x)
 print(x.item())

tensor([0.2206])
0.22063039243221283

Numpy Bridge

PyTorch 张量和 Numpy 数组之间可以很容易地进行转换。

如果 Tensor 运行在 CPU 上，那么 Tensor 和 NumPy 数组可以共享同一内存。改变内存中的数值会同时影响到 Tensor 和 Numpy 数组。

将 Tensor 转换为 NumPy 数组

 a = torch.ones(5)
 print(a)
 b = a.numpy()
 print(b)
 a.add_(1)
 print(a)
 print(b)

tensor([., ., ., ., .])
[. . . . .]
tensor([., ., ., ., .])
[. . . . .]

将 NumPy 数组转换为 Tensor

 import numpy as np
 a = np.ones(5)
 b = torch.from_numpy(a)
 np.add(a, 1, out=a)
 print(a)
 print(b)

[. . . . .]
tensor([., ., ., ., .], dtype=torch.float64)

CUDA 张量

使用 .to 方法，张量可以移动到任何设备上（如 CUDA）。

 # let us run this cell only if CUDA is available
 # We will use ``torch.device`` objects to move tensors in and out of GPU
 if torch.cuda.is_available():
     device = torch.device('cuda')  # 一个 CUDA 设备对象
     y = torch.ones_like(x, device=device)  # 直接在 GPU 上创建一个张量
     x = x.to(device)                       # 或者使用 .to('cuda')
     z = x + y
     print(z)
     print(z.to('cpu', torch.double))       # to 也可以同时修改 dtype

tensor([-0.0786], device='cuda:0')
tensor([-0.0786], dtype=torch.float64)

AUTOGRAD：自动求导

在所有 PyTorch 的神经网络中，最核心的就是 autograd 包。我们首先简单了解一下它，其后我们会训练一个自己的神经网络。

autograd 包对于张量的运算提供了自动求导功能。

张量

torch.Tensor 是该包的核心类。如果你设定它的属性 .requires_grad 为 True，那么它会追踪张量的所有运算。结束运算时，调用 .backward() 可以自动计算所有的梯度。该张量的梯度会聚合到 .grad 属性中。

如果需要停止追踪，你需要调用 .detach() 将张量对计算历史解绑，避免后续计算的追踪。

除了上面的方法，你还可以把代码块封装在 with torch.no_grad(): 中。这在评估模型时非常有用，因为模型可能会有 require_grad=True 的参数，但是我们并不需要它们的梯度。

自动求导的实现中，还有一个类非常重要：Function。

Tensor 和 Function 相互关联，构建一张非循环的图，这张图编码了完整的计算历史。每个张量有一个 .grad_fn 属性来引用一个创建该张量的 Function。

如果你需要计算导数，可以调用 Tensor 的 .backward() 方法。

创建一个 requires_grad=True 的张量：

 x = torch.ones(2, 2, requires_grad=True)
 print(x)

tensor([[., .],
        [., .]], requires_grad=True)

进行张量运算：

 y = x + 2
 print(y)

tensor([[., .],
        [., .]], grad_fn=<AddBackward0>)

y 是运算的结果，因此它有 grad_fn 属性。

 print(y.grad_fn)

<AddBackward0 object at 0x7f3287a29390>

进行更多运算：

 z = y * y * 3
 out = z.mean()

 print(z, out)

tensor([[., .],
        [., .]], grad_fn=<MulBackward0>) tensor(., grad_fn=<MeanBackward0>)

.requires_grad_(...) 会原地改变当前张量的 requires_grad 标记。

 a = torch.randn(2, 2)
 a = ((a * 3) / (a - 1))
 print(a.requires_grad)
 a.requires_grad_(True)
 print(a.requires_grad)
 b = (a * a).sum()
 print(b.grad_fn)

False
True
<SumBackward0 object at 0x7f3287a18908>

梯度

让我们进行后馈操作。由于 out 包含一个标量，out.backward() 等价于 out.backward(torch.tensor(1.))。

 out.backward()

打印梯度 d(out)/dx：

 print(x)
 print(out)
 print(x.grad)

tensor([[., .],
        [., .]], requires_grad=True)
tensor(., grad_fn=<MeanBackward0>)
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

我们来验证一下这个结果。我们计算的梯度是 $\frac{\partial out}{\partial x_i}$，而

$$out =  \frac{1}{4}\sum z_{i}$$

并且

$$z_i=3\times y^2=3\times(x+2)^2$$

因此

$$\frac{\partial out}{\partial x_i}=\frac{\partial out}{\partial z_i}\frac{\partial z_i}{\partial x_i}=\frac{1}{4}\times 6(x+2)=\frac{3(x+2)}{2}$$

由于 $x_i=1$，代入可以得到

$$\frac{\partial out}{\partial x_i}|_{i=1}=4.5$$

我们在从矩阵的意义上去理解：如果有一个向量函数 $\vec{y}=f(\vec{x})$，那么 $\vec{y}$ 对于 $\vec{x}$ 的梯度是一个 Jacobian 矩阵：

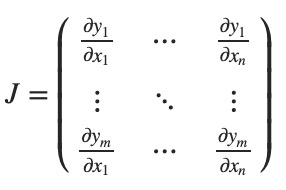
大体上讲，torch.autograd 就是计算向量-Jacobian矩阵的内积的引擎。给定 $v=(v_1, v_2, ..., v_m)^T$，计算内积 $J^Tv$。如果 v 正好是标量函数的梯度 $l=g(\vec y)$，即 $v=(\frac{\partial l}{\partial y_1}, ...,\frac{\partial l}{\partial y_m})^T$，那么这个向量-Jacobian矩阵的内积就等于 $l$ 对于 $\vec x$ 的导数：

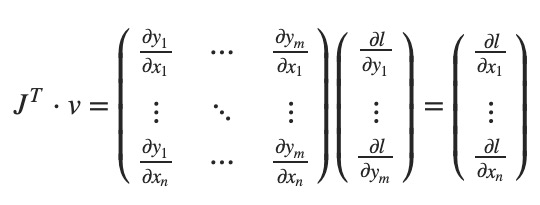
下面看一个向量-Jacobian内积的例子：

 x = torch.randn(3, requires_grad=True)
 y = x * 2
 while y.data.norm() < 1000:
     y = y * 2

 print(y)

tensor([-886.5914,   41.8782, 1542.3958], grad_fn=<MulBackward0>)

现在由于 y 不是标量，torch.autograd 不能直接计算整个 Jacobian 矩阵。但是如果希望求得向量-Jacobian的内积，可以向 backward 传入一个向量参数。

 v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
 y.backward(v)

 print(x.grad)

tensor([4.0960e+02, 4.0960e+03, 4.0960e-01])

可以用 with torch.no_grad(): 来封装代码块：

 print(x.requires_grad)
 print((x ** 2).requires_grad)

 with torch.no_grad():
     print((x ** 2).requires_grad)

True
True
False

神经网络

我们可以使用 torch.nn 包来构建神经网络。

nn 依赖于 autograd 来定义模型并且对模型求导。nn.Module 包含神经网络层以及一个 forward(input) 方法返回输出。

例如下面分类数字图片的神经网络：

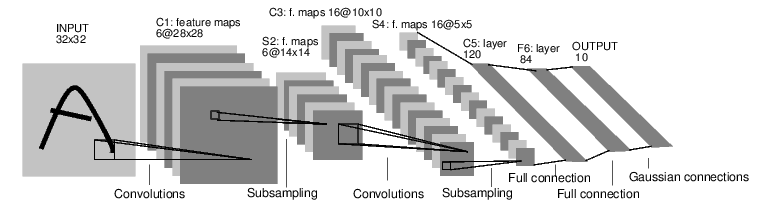
这是一个简单的前馈神经网络。一个神经网络的传统训练方法是：

• 定义含有一些可以学习的参数（或权重）的神经网络。
• 遍历一个输入数据集。
• 将输入向前传入神经网络。
• 计算损失。
• 向后传播梯度到神经网络的参数。
• 更新神经网络的参数，通常使用简单的更新规则： weight = weight - learning_rate * gradient

定义神经网络

 import torch
 import torch.nn as nn
 import torch.nn.functional as F

 class Net(nn.Module):

     def __init__(self):
         super(Net, self).__init__()
         # 1 input image channel, 6 output channels, 3x3 square convolution
         # kernel
         self.conv1 = nn.Conv2d(1, 6, 3)
         self.conv2 = nn.Conv2d(6, 16, 3)
         # an affine operation: y = Wx + b
         self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension
         self.fc2 = nn.Linear(120, 84)
         self.fc3 = nn.Linear(84, 10)

     def forward(self, x):
         # Max pooling over a (2, 2) window
         x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
         # If the size is a square you can only specify a single number
         x = F.max_pool2d(F.relu(self.conv2(x)), 2)
         x = x.view(-1, self.num_flat_features(x))
         x = F.relu(self.fc1(x))
         x = F.relu(self.fc2(x))
         x = self.fc3(x)
         return x

     def num_flat_features(self, x):
         size = x.size()[1:]  # all dimensions except the batch dimension
         num_features = 1
         for s in size:
             num_features *= s
         return num_features

 net = Net()
 print(net)

Net(
  (conv1): Conv2d(, , kernel_size=(, ), stride=(, ))
  (conv2): Conv2d(, , kernel_size=(, ), stride=(, ))
  (fc1): Linear(in_features=, out_features=, bias=True)
  (fc2): Linear(in_features=, out_features=, bias=True)
  (fc3): Linear(in_features=, out_features=, bias=True)
)

这里我们定义了 forward 函数，而 backward 函数（计算梯度）可以使用 autograd 自动定义。

学习好的模型参数可以通过 net.parameters() 返回。

 params = list(net.parameters())
 print(len(params))
 print(params[0].size())  # conv1's .weight

torch.Size([, , , ])

接下来我们尝试随机的 32*32 输入（LeNet 所设置的输入大小是 32*32）。

 input = torch.randn(1, 1, 32, 32)
 out = net(input)
 print(out)

tensor([[-0.0236, -0.0104,  0.0173, -0.1874, -0.0613, -0.0162, -0.1466,  0.1535,
          0.0596, -0.0320]], grad_fn=<AddmmBackward>)

在进一步学习之前，这里再回顾一下你看过的类。

• torch.Tensor：支持自动求导运算（backward()）的多维数组。同时它也保存着梯度信息。
• nn.Module：神经网络模块。可以很容易地封装参数、放到 GPU 进行运算、导出和加载等。
• nn.Parameter：某种张量，当赋值为 Module 的属性时，可以自动注册为参数。
• autograd.Function：实现自动求导运算的前馈和后馈的定义。每个 Tensor 运算会创建至少一个 Function 节点（创建该 Tensor 的函数）。

到目前为止，我们讲解了：

• 定义一个神经网络
• 处理输入并且调用后馈运算

我们还需要：

• 计算损失（loss）
• 更新神经网络的权重

损失函数

损失函数接收输入的 (output, target) 对，计算出 output 与 target 之间的差值。

在 nn 包中有很多不同的损失函数。 最简单的是 nn.MSELoss，计算出两者的均方误差。

 output = net(input)
 target = torch.randn(10)  # a dummy target, for example
 target = target.view(1, -1)  # make it the same shape as output
 criterion = nn.MSELoss()

 loss = criterion(output, target)
 print(loss)

tensor(0.6006, grad_fn=<MseLossBackward>)

我们可以查看反向传播的各层的运算：

 print(loss.grad_fn)  # MSELoss
 print(loss.grad_fn.next_functions[0][0])  # Linear
 print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

<MseLossBackward object at 0x7f3280404588>
<AddmmBackward object at 0x7f32804047f0>
<AccumulateGrad object at 0x7f3280404588>

反向传播

我们使用 loss.backward() 进行误差的反向传播。但是你需要清除现有的梯度，否则梯度会已存在的梯度上累积。

我们调用 loss.backward()，并且观察 conv1 的偏差的梯度的变化。

 net.zero_grad()  # zeroes the gradient buffers of all parameters

 print('conv1.bias.grad before backward')
 print(net.conv1.bias.grad)

 loss.backward()

 print('conv1.bias.grad after backward')
 print(net.conv1.bias.grad)

conv1.bias.grad before backward
None
conv1.bias.grad after backward
tensor([ 3.5922e-03,  7.0686e-03,  3.9444e-03,  1.1225e-02, -5.1291e-03,
        -6.0605e-05])

权重的更新

实践中最简单的更新方法是随机梯度下降（Stochastic Gradient Descent, SGD）：

weight = weight - learning_rate * gradient

我们可以用简单的 Python 代码来实现：

 learning_rate = 0.01
 for f in net.parameters():
     f.data.sub_(f.grad.data * learning_rate)

然而，使用神经网络的时候，你可能会使用不同的更新方法（SGD、Nesterov-SGD、Adam、RMSProp 等）。为了满足这方面的需求，PyTorch 构建了一个包：torch.optim 实现了所有这些方法。

 import torch.optim as optim

 # create your optimizer
 optimizer = optim.SGD(net.parameters(), lr=0.01)

 # in your training loop:
 optimizer.zero_grad()  # zero the gradient buffers
 output = net(input)
 loss = criterion(output, target)
 loss.backward()
 optimizer.step()  # Does the update

训练一个分类器

前面我们已经可以定义神经网络、计算损失并且更新神经网络的权重了。

那么什么是数据？

通常，当处理图像、文本、音频或者视频数据时，你可以使用标准 Python 包来将数据加载为 Numpy 数组。接着你可以把 NumPy 数组转换为 torch.*Tensor。

• 对于图片，可能使用 Pillow/OpenCV 这些包
• 对于音频，可能使用 scipy/librosa 这些包
• 对于文本，可以使用 Python/Cython/NLTK/SpaCy 进行处理

对于计算机视觉，PyTorch 提供了一个叫 torchvision 的包，可以加载常见的数据集（imagenet/CIFAR10/MNIST 等），对图片进行数据转换。

在这里，我们会使用 CIFAR10 数据集。它有这几个种类：airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck。CIFAR-10 的图片大小都是 3*32*32。

训练图片分类器

我们的步骤是这样的：

1. 使用 torchvision 加载并且标准化 CIFAR10 的训练接和数据集。
2. 定义一个卷积神经网络。
3. 定义损失函数。
4. 在训练集上训练神经网络。
5. 在测试集上训练神经网络。

1. 加载并标准化 CIFAR10

使用 torchvision，要加载 CIFAR10 很容易。

 import torch
 import torchvision
 import torchvision.transforms as transforms

torchvision 数据集的输出是范围 0~1 的 PIL 图片。我们将它标准化，范围 -1~1。

 transform = transforms.Compose([
     transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
 ])

 trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
 trainloader = torch.utils.data.DataLoader(trainset, batch_size=4, shuffle=True, num_workers=2)
 testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
 testloader = torch.utils.data.DataLoader(testset, batch_size=4, shuffle=False, num_workers=2)
 classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

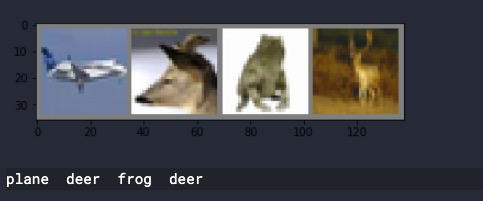
下面显示部分训练图片：

 import matplotlib.pyplot as plt
 import numpy as np

 # functions to show an image

 def imshow(img):
     img = img / 2 + 0.5     # unnormalize
     npimg = img.numpy()
     plt.imshow(np.transpose(npimg, (1, 2, 0)))
     plt.show()

 # get some random training images
 dataiter = iter(trainloader)
 images, labels = dataiter.next()

 # show images
 imshow(torchvision.utils.make_grid(images))
 # print labels
 print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

2. 定义卷积神经网络

 import torch.nn as nn
 import torch.nn.functional as F

 class Net(nn.Module):
     def __init__(self):
         super(Net, self).__init__()
         self.conv1 = nn.Conv2d(3, 6, 5)
         self.pool = nn.MaxPool2d(2, 2)
         self.conv2 = nn.Conv2d(6, 16, 5)
         self.fc1 = nn.Linear(16 * 5 * 5, 120)
         self.fc2 = nn.Linear(120, 84)
         self.fc3 = nn.Linear(84, 10)

     def forward(self, x):
         x = self.pool(F.relu(self.conv1(x)))
         x = self.pool(F.relu(self.conv2(x)))
         x = x.view(-1, 16 * 5 * 5)
         x = F.relu(self.fc1(x))
         x = F.relu(self.fc2(x))
         x = self.fc3(x)
         return x

 net = Net()
 print(net)

Net(
  (conv1): Conv2d(, , kernel_size=(, ), stride=(, ))
  (pool): MaxPool2d(kernel_size=, stride=, padding=, dilation=, ceil_mode=False)
  (conv2): Conv2d(, , kernel_size=(, ), stride=(, ))
  (fc1): Linear(in_features=, out_features=, bias=True)
  (fc2): Linear(in_features=, out_features=, bias=True)
  (fc3): Linear(in_features=, out_features=, bias=True)
)

3. 定义损失函数和优化器

我们使用分类交叉熵和动量 SGD。

 import torch.optim as optim

 criterion = nn.CrossEntropyLoss()
 optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

4. 训练网络

 %%time
 for epoch in range(4):  # loop over the dataset multiple times

     running_loss = 0.0
     for i, data in enumerate(trainloader, 0):
         # get the inputs; data is a list of [inputs, labels]
         inputs, labels = data

         # zero the parameter gradients
         optimizer.zero_grad()

         # forward + backward + optimize
         outputs = net(inputs)
         loss = criterion(outputs, labels)
         loss.backward()
         optimizer.step()

         # print statistics
         running_loss += loss.item()
         if i % 2000 == 1999:    # print every 2000 mini-batches
             print('[%d, %5d] loss: %.3f' %
                   (epoch + 1, i + 1, running_loss / 2000))
             running_loss = 0.0

 print('Finished Training')

[,  ] loss: 2.223
[,  ] loss: 1.949
[,  ] loss: 1.754
[,  ] loss: 1.622
[, ] loss: 1.544
[, ] loss: 1.496
[,  ] loss: 1.412
[,  ] loss: 1.386
[,  ] loss: 1.373
[,  ] loss: 1.335
[, ] loss: 1.327
[, ] loss: 1.295
[,  ] loss: 1.221
[,  ] loss: 1.239
[,  ] loss: 1.255
[,  ] loss: 1.193
[, ] loss: 1.186
[, ] loss: 1.203
[,  ] loss: 1.126
[,  ] loss: 1.140
[,  ] loss: 1.120
[,  ] loss: 1.122
[, ] loss: 1.112
[, ] loss: 1.114
Finished Training
CPU times: user 3min 34s, sys: 45.6 s, total: 4min 20s
Wall time: 4min 49s

5. 在测试集上测试网络

我们对神经网络训练了 2 次，接下来要看一下该网络是否学习到了东西。

首先展示测试集的几张图片。

接下来让我们看一下神经网络认为这几张图片是啥。

 _, predicted = torch.max(outputs, 1)

 print('Predicted: ', ' '.join('%5s' % classes[predicted[j]] for j in range(4)))

Predicted:    cat  ship plane   car

结果看起来还凑合。

接下来我们看一下在整个测试集上神经网络表现得如何。

 correct = 0
 total = 0
 with torch.no_grad():
     for data in testloader:
         images, labels = data
         outputs = net(images)
         _, predicted = torch.max(outputs.data, 1)
         total += labels.size(0)
         correct += (predicted == labels).sum().item()

 print('Accuracy of the network on the 10000 test images: %d %%' % (100 * correct / total))

Accuracy of the network on the  test images:  %

再看看每个分类下的表现：

 class_correct = list(0. for i in range(10))
 class_total = list(0. for i in range(10))
 with torch.no_grad():
     for data in testloader:
         images, labels = data
         outputs = net(images)
         _, predicted = torch.max(outputs, 1)
         c = (predicted == labels).squeeze()
         for i in range(4):
             label = labels[i]
             class_correct[label] += c[i].item()
             class_total[label] += 1

 for i in range(10):
     print('Accuracy of %5s : %2d %%' % (
         classes[i], 100 * class_correct[i] / class_total[i]))

Accuracy of plane :  %
Accuracy of   car :  %
Accuracy of  bird :  %
Accuracy of   cat :  %
Accuracy of  deer :  %
Accuracy of   dog :  %
Accuracy of  frog :  %
Accuracy of horse :  %
Accuracy of  ship :  %
Accuracy of truck :  %

在 GPU 上进行训练

就像之前我们把张量放到 GPU 上一样，我们需要把神经网络也放在 GPU。

如果我们有 CUDA，先定义设备：

 device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

 # Assuming that we are on a CUDA machine, this should print a CUDA device:
 print(device)

cuda:

查看可以使用的 GPU 数量：

 print(torch.cuda.device_count())

1

然后注意把模型和输入数据放入 GPU 进行训练：

 %%time
 net.to(device)
 for epoch in range(4):  # loop over the dataset multiple times

     running_loss = 0.0
     for i, data in enumerate(trainloader, 0):
         # get the inputs; data is a list of [inputs, labels]
         inputs, labels = data
         inputs, labels = inputs.to(device), labels.to(device)

         # zero the parameter gradients
         optimizer.zero_grad()

         # forward + backward + optimize
         outputs = net(inputs)
         loss = criterion(outputs, labels)
         loss.backward()
         optimizer.step()

         # print statistics
         running_loss += loss.item()
         if i % 2000 == 1999:    # print every 2000 mini-batches
             print('[%d, %5d] loss: %.3f' %
                   (epoch + 1, i + 1, running_loss / 2000))
             running_loss = 0.0

 print('Finished Training')

[1,  2000] loss: 2.225
[1,  4000] loss: 1.895
[1,  6000] loss: 1.678
[1,  8000] loss: 1.565
[1, 10000] loss: 1.508
[1, 12000] loss: 1.467
[2,  2000] loss: 1.393
[2,  4000] loss: 1.349
[2,  6000] loss: 1.319
[2,  8000] loss: 1.317
[2, 10000] loss: 1.322
[2, 12000] loss: 1.255
[3,  2000] loss: 1.191
[3,  4000] loss: 1.200
[3,  6000] loss: 1.230
[3,  8000] loss: 1.190
[3, 10000] loss: 1.162
[3, 12000] loss: 1.167
[4,  2000] loss: 1.096
[4,  4000] loss: 1.102
[4,  6000] loss: 1.089
[4,  8000] loss: 1.099
[4, 10000] loss: 1.092
[4, 12000] loss: 1.066
Finished Training
CPU times: user 2min 27s, sys: 20.2 s, total: 2min 47s
Wall time: 3min 33s

加速效果跟神经网络的大小有关系，不适用 GPU 需要 4 分 49 秒，我们的 GPU 版本消耗时间 3 分 33 秒。我们目前的神经网络还比较小，因此加速效果并不是非常大。