回顾二分与bfs（或者说是递推）和简单模拟

今天，阳光正好，适合敲代码，诸事皆宜。

先来两道简单的模拟题。

第一道

机器翻译

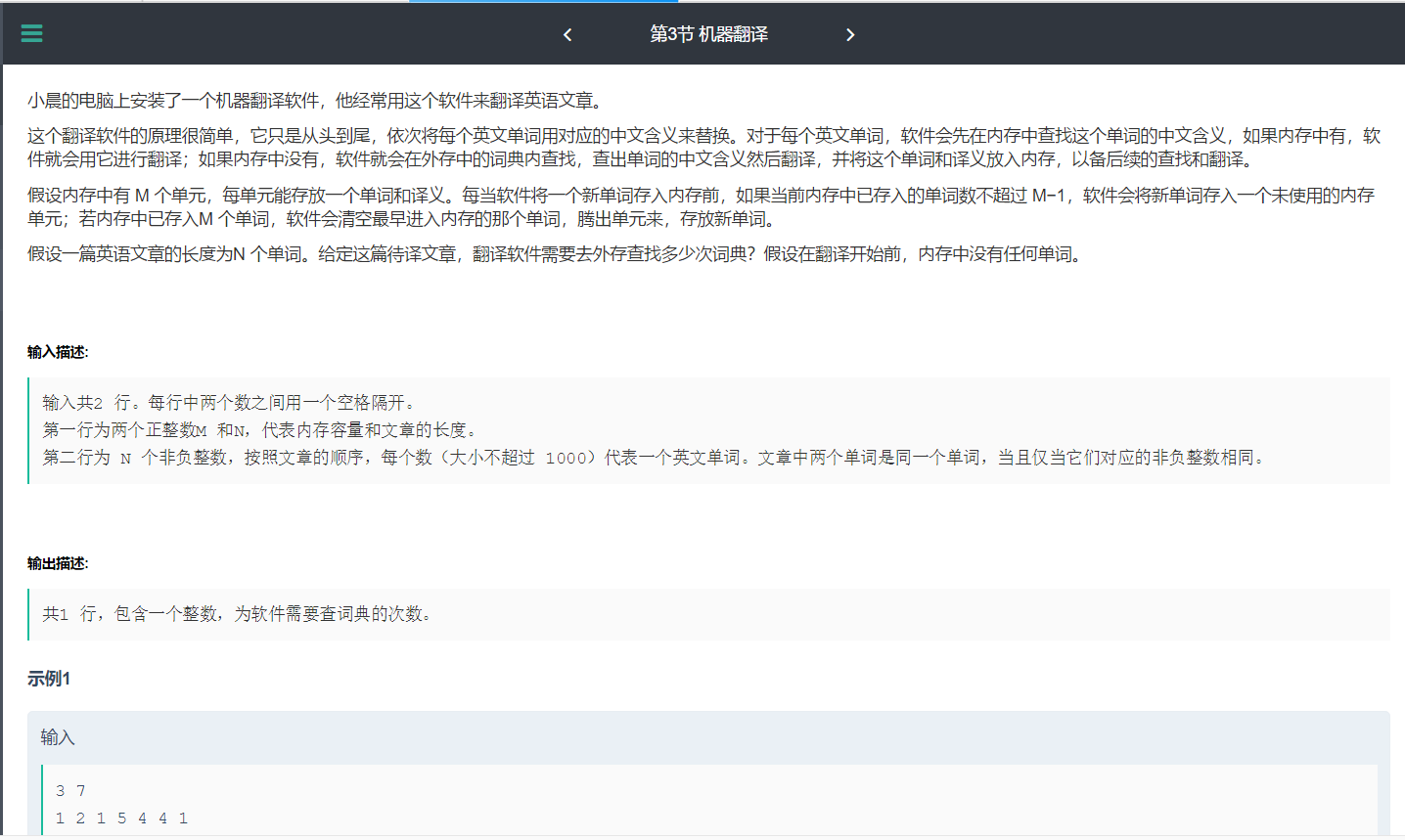
输出为5.

代码思路：很明显需要用到队列来存单词，在建立一个bool数组来存储队列中有没有这个单词，需不需要向外界查询，如果需要并且队列可以容下，则加入队列并将bool数组标记在队列中有该单词，如果队列容不下，则将队头弹出，并用bool数组标记弹出的数字在该队列中没有。

代码：

#include<bits/stdc++.h>
using namespace std;
queue<int> ss;
bool mp[];
int n,m;
int main()
{
    int i,j,t,ans=;
    cin>>m>>n;
    for(i=;i<n;i++)
    {
        cin>>t;
        if(ss.size()>m)
        {
            int f=ss.front();
            mp[f]=;
            ss.pop();
        }
        if(mp[t]==)
        {
            ss.push(t);
            ans++;
            mp[t]=;
        }
    }
    cout<<ans<<endl;
    return ;
}

第二道

神奇的幻方

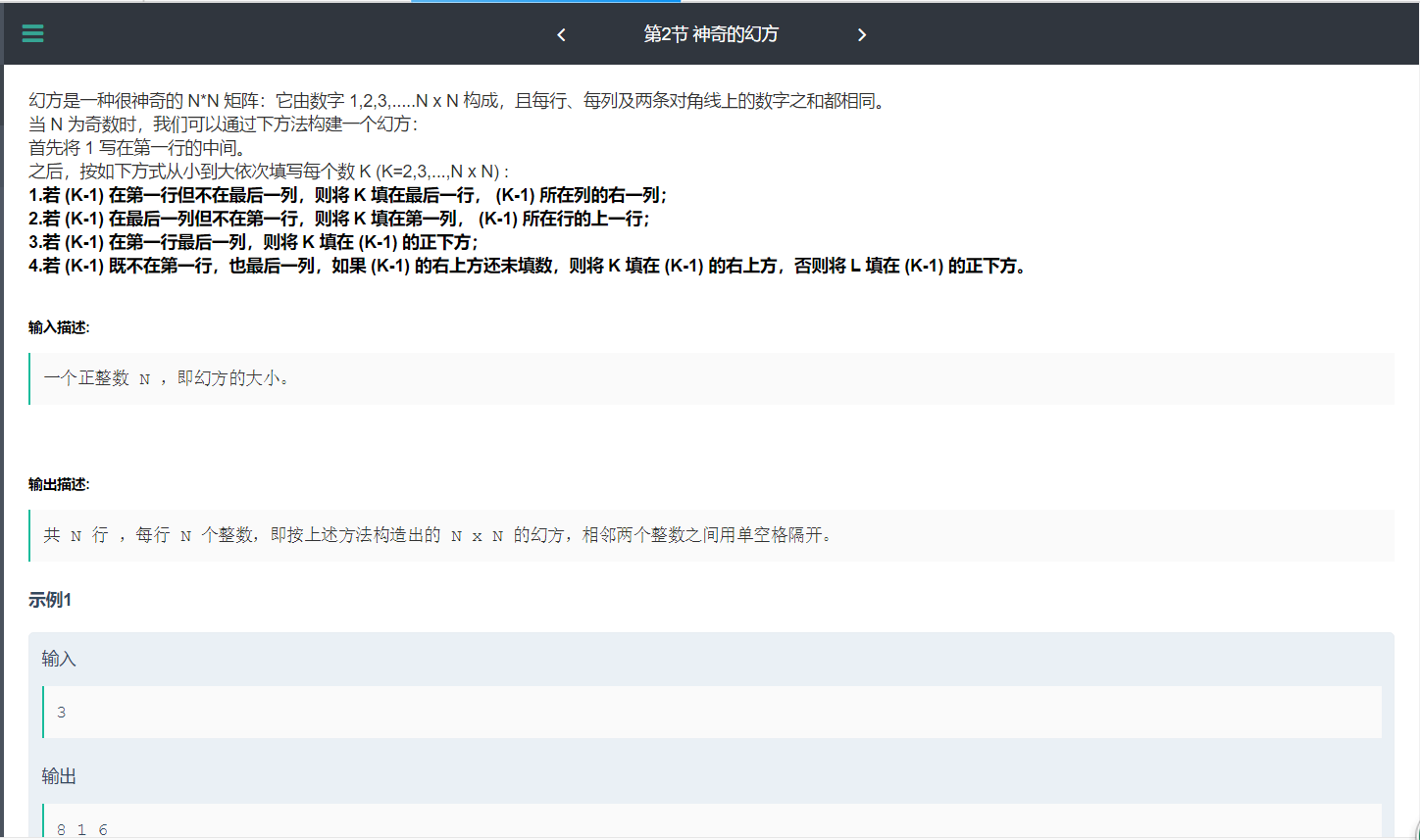
输出为：

8 1 6
3 5 7
4 9 2
思路：按题中步骤执行即可
首先找到1的位置，他在x=1，y=n/2+1;
然后判断若x在第一行，但不在最后一列，就让下一个数在x=n,y++的位置;
若不在第一行，在最后一列，就让下一个数在x--,y=1的位置；
若在第一行最后一列，就让下一个数在x++,y的位置；
若既不在最后一行也不在最后一列，并且右上方没有数字，则下一个数在x--,y++的位置；
以上四个都不满足就在x++,y的位置；
代码：

#include<bits/stdc++.h>
using namespace std;
int a[][];
int main()
{
    int n,i,j,x,y;
    cin>>n;
    x=;y=n/+;
    for(i=;i<=n*n;i++)
    {
        a[x][y]=i;
        if(x==&&y!=n)
        {
            x=n;y++;
        }
        else if(y==n&&x!=)
        {
            y=;x--;
        }
        else if(x==&&y==n)
        {
            x++;
        }
        else if(a[x-][y+]==)
        {
            x--;y++;
        }
        else
            x++;
    }
    for(i=;i<=n;i++)
    {
        for(j=;j<=n;j++)
            cout<<a[i][j]<<" ";
        cout<<endl;
    }
    return ;
}

一道二分的题

灵能探索

链接：https://ac.nowcoder.com/acm/contest/639/A
来源：牛客网
思路：二分边界是从[灵能的最小值,灵能总和]，check()函数的书写：循环数组，累加如果大于等于mid的值，则让con++，s=0，继续循环直到结束。判断con的值是否大于等于题中输入的组数，大于返回1，证明mid的值还可以在大，就让l=mid+1,ans=mid，如果con的值不大于，证明mid的值大了，则需要r=mid-1,在进行判断找出合适的mid的值。

代码：

#include<bits/stdc++.h>
using namespace std;
const long long N=;
long long n,k,ans,a[N];
long long check(long long x)
{
    long long i,j,s=,con=;
    for(i=;i<n;i++)
    {
        s+=a[i];
        if(s>=x)
        {
            con++;
            s=;
        }
    }
    if(con>=k)
        return ;
    return ;
}
int main()
{
    long long i,j,minx=,sum=;
    long long l,r,mid;
    cin>>n>>k;
    for(i=;i<n;i++)
    {
        cin>>a[i];
        minx=min(minx,a[i]);
        sum+=a[i];
    }
    l=minx;r=sum;
    while(l<=r)
    {
        mid=(l+r)/;
        if(check(mid))
        {
            l=mid+;
            ans=mid;
        }
        else
            r=mid-;
    }
    cout<<ans<<endl;
}

一个乍一看是一道bfs搜索题，然而他却是到递推题。

好心酸。。。。。

过河卒

链接：https://ac.nowcoder.com/acm/contest/639/B
来源：牛客网

先说说bfs的思路：从（1，1）开始搜索，遇到马或者超界就不放入队列里，最后如果队列到达了终点则ans++；

代码：可惜只过了75%的数据

#include<bits/stdc++.h>
using namespace std;
const int mod=;
int n,m,x,y,ans;
int xx[]={,},yy[]={,};
int v[][];
int vis[][];
struct node
{
    int a,b;
};
void bfs(int X,int Y)
{
    vis[X][Y]=;
    node t;
    t.a=X;t.b=Y;
    queue<node> p;
    p.push(t);
    while(!p.empty())
    {
        node g=p.front();
        p.pop();
        if(g.a==n&&g.b==m)
        {
            ans++;
            continue;
        }
        for(int i=;i<;i++)
        {
            int w=g.a+xx[i];
            int l=g.b+yy[i];
            if(v[w][l]!=&&vis[w][l]!=&&w>=&&w<=n&&l>=&&l<=m)
            {
                p.push(node{w,l});
            }
        }
    }
    return ;
}
int main()
{
    int i,j;
    cin>>n>>m>>x>>y;
    v[x][y]=;
    v[x-][y-]=;
    v[x-][y-]=;
    v[x-][y+]=;
    v[x-][y+]=;

    v[x+][y-]=;
    v[x+][y-]=;
    v[x+][y+]=;
    v[x+][y+]=;
    bfs(,);
    cout<<ans%mod<<endl;
    return ;
}

正解：递推dp[i][j]=dp[i-1][j]+dp[i][j-1]

现将马的所有可去的位置用v[][]的二维数组标记上，然后将表格的第一行和第一列dp[][]赋值为1，如果途中遇到马的位置，则停下结束循环，马下面的将不会走故而可以结束循环，最终用二重循环从（2，2）开始计算如果不是马的位置则dp[i][j]=(dp[i-1][j]+dp[i][j-1])%mod，否则dp[i][j]=0;

最终输出dp[n][m]%mod的值，在这里特别声明一定要在计算dp[i][j]的时候也要取mod，因为数字很大容易超限，导致错误。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=;
ll n,m,ans,x,y;
int x1[]={,-,-,,,,,-,-};
int yy[]={,,,,,-,-,-,-};
ll dp[][];
ll v[][];
int main()
{
    ll i,j;
    cin>>n>>m>>x>>y;
    v[x][y]=;
    for(i=;i<=;i++)
    {
        if(x+x1[i]>=&&y+yy[i]>=)
            v[x+x1[i]][y+yy[i]]=;
    }
    for(i=;i<=n;i++)
    {
        if(v[i][]==)
            dp[i][]=;
        else
            break;
    }
    for(j=;j<=m;j++)
    {
        if(v[][j]==)
            dp[][j]=;
        else
            break;
    }
    for(i=;i<=n;i++)
    {
        for(j=;j<=m;j++)
        {
            if(v[i][j]==)
                dp[i][j]=(dp[i-][j]+dp[i][j-])%mod;
            else
                dp[i][j]=;
        }
    }
    cout<<dp[n][m]%mod<<endl;
    return ;
}

ACM之旅仍在继续，加油！！少年