数据结构-哈夫曼树（python实现）

好，前面我们介绍了一般二叉树、完全二叉树、满二叉树，这篇文章呢，我们要介绍的是哈夫曼树。

哈夫曼树也叫最优二叉树，与哈夫曼树相关的概念还有哈夫曼编码，这两者其实是相同的。哈夫曼编码是哈夫曼在1952年提出的。现在哈夫曼编码多应用在文本压缩方面。接下来，我们就来介绍哈夫曼树到底是个什么东西？哈夫曼编码又是什么，以及它如何应用于文本压缩。

哈夫曼树（Huffman Tree）

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

首先，我们有这样一些数据：

sourceData = [('a', 8), ('b', 5), ('c', 3), ('d', 3), ('e', 8), ('f', 6), ('g', 2), ('h', 5), ('i', 9), ('j', 5), ('k', 7), ('l', 5), ('m', 10), ('n', 9)]

每一个数据项是一个元组，元组的第一项是数据内容，第二项是该数据的权重。也就是说，用于构建哈夫曼树的数据是带权重的。假设这些数据里面的字母a-n的权重是根据这些字母在y一个文本出出现的概率计算得出的，字母出现的概率越高，则该字母的权重越大。例如字母 a 的权重为 8 .

好，拿到数据我们就可以来构建哈夫曼树了。

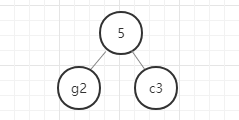
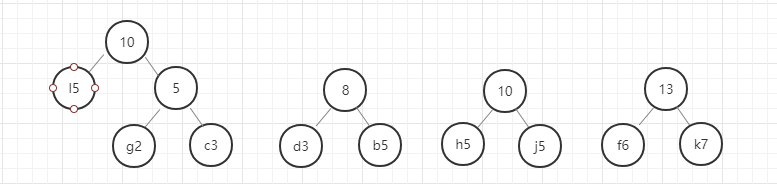
1. 首先，找出所有元素中权重最小的两个元素，即g(2)和c(3)，
2. 以g和c为子节点构建二叉树，则构建的二叉树的父节点的权重为 2+3 = 5.
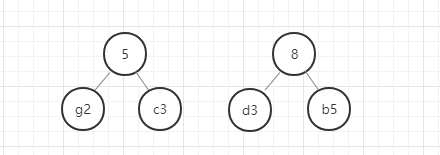
3. 从除g和c以外剩下的元素和新构建的权重为5的节点中选出权重最小的两个节点，
4. 进行第 2 步操作。

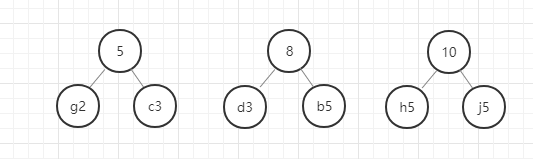
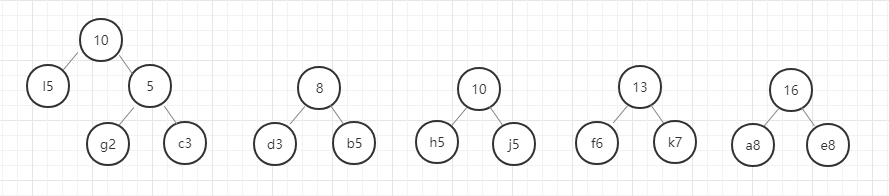
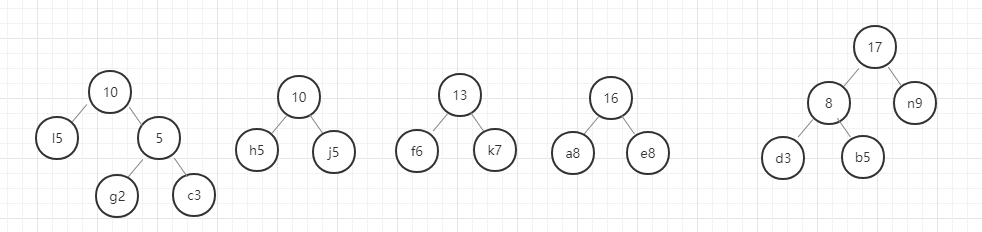
以此类推，直至最后合成一个二叉树就是哈夫曼树。

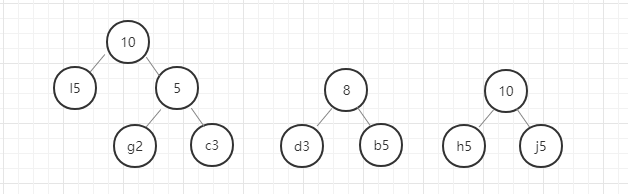
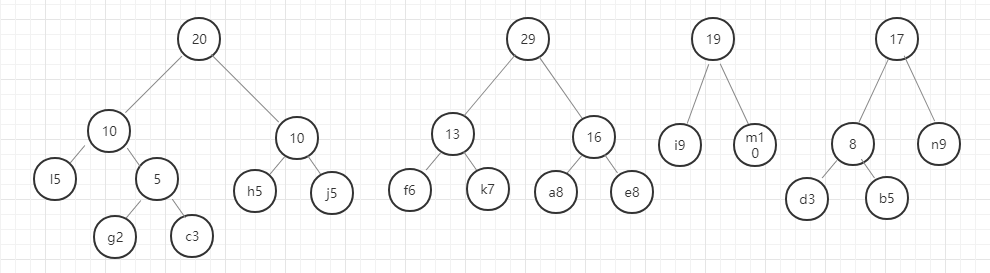
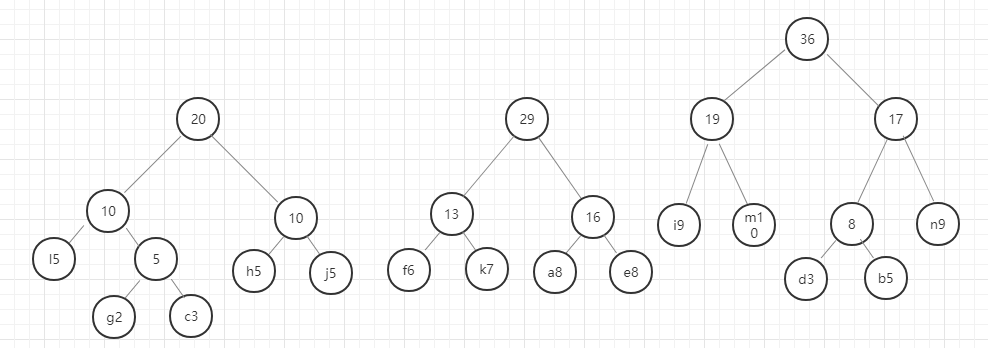
我们用图例来表示一下：

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 

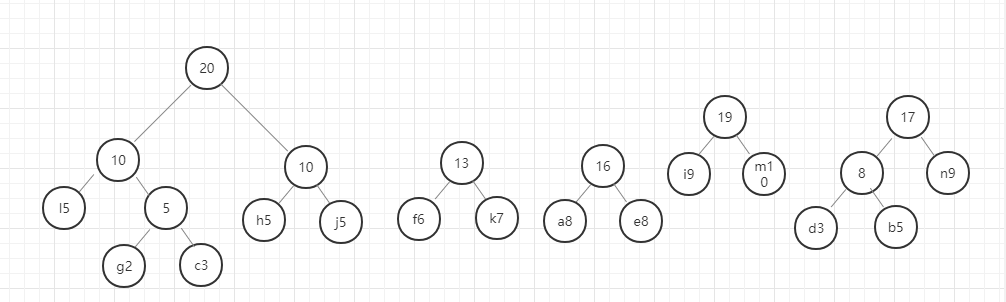
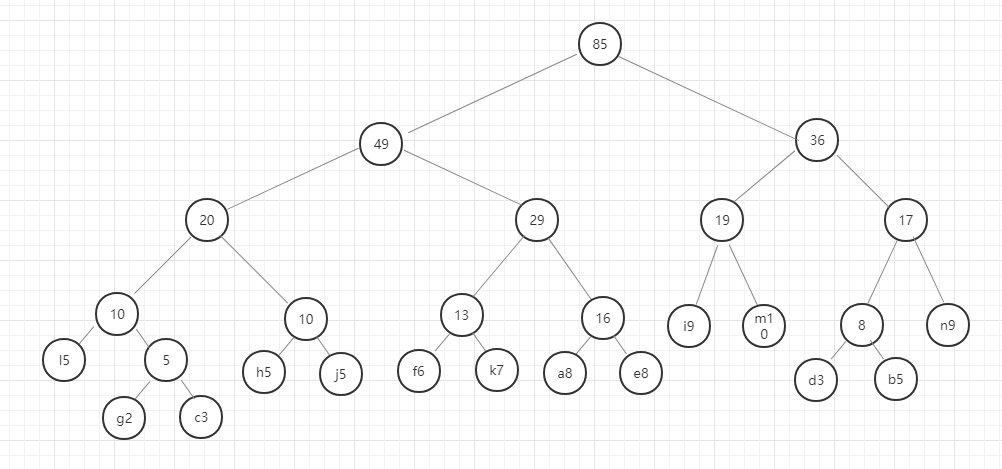
好，这里我们的哈夫曼树就构建好了，节点中字母后面的数字表示该字母的权重，就是前面给定的数据。在这里我要强调的是，同样的数据创建的哈夫曼树并不是唯一的，所以只要按照规则一步一步没有出错，你的哈夫曼树就是正确的。

我们现在将访问左节点定义为0，访问右节点定义为1.则我们现在访问字母a，则它的编码为0110，访问字母n的编码为111，这个编码就是哈夫曼编码。

通过比对不同字母的哈夫曼编码，你发现了什么？

权重越大的字母对应的哈夫曼编码越短，权重越小的字母对应的哈夫曼编码则越长。也就是说文本中出现概率大的字母编码短，出现概率小的字母编码长。通过这种编码方式来表示文本中的字母，那所得整个文本的编码长度也会缩短。

这就是哈夫曼树也就是哈夫曼编码在文本压缩中的应用。

下面我们用代码来实现：

定义一个二叉树类：

class BinaryTree:
    def __init__(self, data, weight):
        self.data = data
        self.weight = weight
        self.left = None
        self.right = None

获取节点列表中权重最小的两个节点：

# 定义获取列表中权重最大的两个节点的方法：
def min2(li):
    result = [BinaryTree(None, float('inf')), BinaryTree(None, float('inf'))]
    li2 = []
    for i in range(len(li)):
        if li[i].weight < result[0].weight:
            if result[1].weight != float('inf'):
                li2.append(result[1])
            result[0], result[1] = li[i], result[0]
        elif li[i].weight < result[1].weight:
            if result[1].weight != float('inf'):
                li2.append(result[1])
            result[1] = li[i]
        else:
            li2.append(li[i])
    return result, li2

定义生成哈夫曼树的方法：

def makeHuffman(source):
    m2, data = min2(source)
    print(m2[0].data, m2[1].data)
    left = m2[0]
    right = m2[1]

    sumLR = left.weight + right.weight
    father = BinaryTree(None, sumLR)
    father.left = left
    father.right = right
    if data == []:
        return father
    data.append(father)
    return makeHuffman(data)

定义广度优先遍历方法：

# 递归方式实现广度优先遍历
def breadthFirst(gen, index=0, nextGen=[], result=[]):

    if type(gen) == BinaryTree:
        gen = [gen]
    result.append((gen[index].data, gen[index].weight))
    if gen[index].left != None:
        nextGen.append(gen[index].left)
    if gen[index].right != None:
        nextGen.append(gen[index].right)

    if index == len(gen)-1:
        if nextGen == []:
            return
        else:
            gen = nextGen
            nextGen = []
            index = 0
    else:
        index += 1
    breadthFirst(gen, index, nextGen,result)

    return result

输入数据：

# 某篇文章中部分字母根据出现的概率规定权重
sourceData = [('a', 8), ('b', 5), ('c', 3), ('d', 3), ('e', 8), ('f', 6), ('g', 2), ('h', 5), ('i', 9), ('j', 5), ('k', 7), ('l', 5), ('m', 10), ('n', 9)]
sourceData = [BinaryTree(x[0], x[1]) for x in sourceData]

创建哈夫曼树并进行广度优先遍历：

huffman = makeHuffman(sourceData)
print(breadthFirst(huffman))

OK ，我们的哈夫曼树就介绍到这里了，你还有什么不懂的问题记得留言给我哦。