【欧拉降幂】Super_log

In Complexity theory, some functions are nearly O(1)O(1), but it is greater then O(1)O(1). For example, the complexity of a typical disjoint set is O(nα(n))O(nα(n)). Here α(n)α(n) is Inverse Ackermann Function, which growth speed is very slow. So in practical application, we often assume α(n) \le 4α(n)≤4.

However O(α(n))O(α(n)) is greater than O(1)O(1), that means if nn is large enough, α(n)α(n) can greater than any constant value.

Now your task is let another slowly function log*log∗ xx reach a constant value bb. Here log*log∗ is iterated logarithm function, it means “the number of times the logarithm function iteratively applied on xx before the result is less than logarithm base aa”.

Formally, consider a iterated logarithm function log_{a}^*loga∗​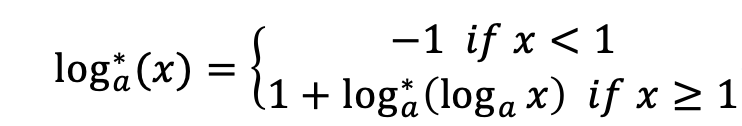

Find the minimum positive integer argument xx, let log_{a}^* (x) \ge bloga∗​(x)≥b. The answer may be very large, so just print the result xx after mod mm.

Input

The first line of the input is a single integer T(T\le 300)T(T≤300) indicating the number of test cases.

Each of the following lines contains 33 integers aa , bb and mm.

1 \le a \le 10000001≤a≤1000000

0 \le b \le 10000000≤b≤1000000

1 \le m \le 10000001≤m≤1000000

Note that if a==1, we consider the minimum number x is 1.

Output

For each test case, output xx mod mm in a single line.

Hint

In the 4-th4−th query, a=3a=3 and b=2b=2. Then log_{3}^* (27) = 1+ log_{3}^* (3) = 2 + log_{3}^* (1)=3+(-1)=2 \ge blog3∗​(27)=1+log3∗​(3)=2+log3∗​(1)=3+(−1)=2≥b, so the output is 2727 mod 16 = 1116=11.

样例输入复制

5
2 0 3
3 1 2
3 1 100
3 2 16
5 3 233

样例输出复制

1
1
3
11
223

题解：求a^a^...(b次)%n的结果。因为n与a不一定互质，所以要利用广义欧拉定理进行降幂。

AC代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<set>
#include<cmath>
#include<string>
#include<map>
#include<vector>
#include<ctime>
#include<stack>
using namespace std;
#define mm(a,b) memset(a,b,sizeof(a))
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 2e5 + ;
#define inf 0x3f3f3f3f
const double PI = acos(-1.0);

ll gcd(ll a,ll b){return b==?a:gcd(b,a%b);}

#define Mod(a,b) a<b?a:a%b+b  //根据欧拉定理重定义mod

ll fpow(ll a,ll n,ll mod)
{
    ll res=;
    while(n)
    {
        if(n&) res=Mod(res*a,mod);
        a=Mod(a*a,mod);
        n>>=;
    }
    return res;
}

ll phi(ll x)  //求x的欧拉函数
{
    ll ans=x,tp=sqrt(x);
    for(ll i=;i<=tp;++i)
    {
        if(x%i==)
        {
            ans=ans-ans/i;
            while(x%i==) x/=i;
        }
    }
    if(x>) ans=ans-ans/x;
    return ans;
}

ll solve(ll a,ll b,ll m)
{
    if(m==) return ;
    if(b<=) return fpow(a,b,m);
    ll p=phi(m);
    ll t=solve(a,b-,p);  //递归求解
    ll g=gcd(a,m);
    if(g==||b<p) return fpow(a,t,m);
    else return fpow(a,t+p,m);
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        ll a,b,m;
        scanf("%lld %lld %lld",&a,&b,&m);
        ll ans=solve(a,b,m)%m;
        printf("%lld\n",ans);
    }
    return ;
}