Educational Codeforces Round 73 (Rated for Div. 2)

传送门

A. 2048 Game

乱搞即可。

Code

#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e5 + 5;

int n;
int a[N];

void run() {
    cin >> n;
    int cnt = 0, cnt1 = 0;
    for(int i = 1; i <= n; i++) {
        cin >> a[i];
        if(a[i] > 2048) continue;
        if(a[i] == 1) ++cnt1;
        else {
            cnt += a[i] / 2;
        }
    }
    cnt += cnt1 / 2;
    if(cnt >= 1024) cout << "YES" << '\n';
    else cout << "NO" << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

B. Knights

直接按奇偶分类其实就行，但我写了个\(dfs\)...

Code

#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 105;

int n;
int a[N][N];
int dx[8] = {-2, -2, -1, -1, 2, 2, 1, 1};
int dy[8] = {-1, 1, -2, 2, -1, 1, -2, 2};
bool chk(int x, int y) {
    return x <= n && x >= 1 && y >= 1 && y <= n && a[x][y] == 0;
}

void dfs(int x, int y, int c) {
    a[x][y] = c;
    for(int i = 0; i < 8; i++) {
        int nowx = x + dx[i], nowy = y + dy[i];
        if(chk(nowx, nowy)) dfs(nowx, nowy, 3 - c);
    }
}

void run() {
    memset(a, 0, sizeof(a));
    dfs(1, 1, 1);
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(a[i][j] == 1) cout << 'W';
            else cout << 'B';
        }
        cout << '\n';
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    while(cin >> n) run();
    return 0;
}

C. Perfect Team

直接输出就行，但我写了个二分...

Code

#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e5 + 5;

int c, m, x;

bool chk(int q) {
    int nc = c - q, nm = m - q;
    return nc >= 0 && nm >= 0 && nc + nm + x >= q;
}

void run() {
    cin >> c >> m >> x;
    int ans = min(c, m);
    if(x >= ans) {
        cout << ans << '\n'; return;
    }
    int l = 0, r = 100000002, mid;
    while(l < r) {
        mid = (l + r) >> 1;
        if(chk(mid)) l = mid + 1;
        else r = mid;
    }
    cout << r - 1 << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

D. Make The Fence Great Again

题意：

给出\(n\)个数，现在定义一个好的序列为：对于任意相邻的\(i,j\)，满足\(a_i\not ={a_j}\)。

现在你可以每次将一个数增加\(1\)，代价为\(b_i\)。

问将给出的序列变成好的序列的最小代价为多少。

思路：

• 注意到一个数最多增加两次，因为如果增加的次数大于\(2\)的话，就会有空隙，填补那个空隙就行了。
• 那么定义\(dp[i,j]\)表示考虑了前\(i\)个数，最后一个数增加了\(j\)次的最小代价，直接枚举转移即可。

代码如下：

Code

#include <bits/stdc++.h>
#define INF 2000000000000000000
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 3e5 + 5;

ll dp[N][5];
int n;
int a[N], b[N];

void run() {
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i] >> b[i];
    for(int i = 0; i <= n; i++) for(int j = 0; j < 5; j++) dp[i][j] = INF;
    for(int i = 0; i < 5; i++) dp[0][i] = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j < 4; j++) {
            for(int k = 0; k < 4; k++) {
                if(i == 1 || a[i - 1] + k != a[i] + j) {
                    dp[i][j] = min(dp[i - 1][k] + 1ll * j * b[i], dp[i][j]);
                }
            }
        }
    }
    ll ans = INF;
    for(int i = 0; i < 4; i++) ans = min(ans, dp[n][i]);
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

E. Game With String

题意：

给出一个\(01\)序列，两个人来玩博弈游戏，博弈规则如下：

• \(A\)为先手，\(B\)为后手，给出\(a,b,b<a\)，\(A\)能够将\(a\)个连续的\(a\)个\(0\)变为\(1\)；\(B\)能够将连续的\(b\)个\(0\)变为\(1\)。
• 当有一个人无法操作时，则输掉这场游戏。

现给出长度不超过\(10^5\)的序列，问谁胜谁负。

思路：

感觉很有意思的一道博弈题，跟平时遇到的博弈题不一样。感觉不一样就在于游戏规则对于双方来说都不一样，好像是非平衡博弈？

首先有一个很重要的观察：

• 如果存在一段连续的\(0\)的长度\(x\)满足：\(b\leq x<a\)，那么\(B\)必胜。

简要证明

\(B\)会比\(A\)多一次机会。

\(A\)能搞的\(B\)也能搞；若出现一个局面，\(B\)必须用掉这一次机会，那么说明其它位置肯定不存在一段长度大于等于\(b\)了，自然之后\(A\)不能再搞了。

那么现在考虑，在什么样的局面下，\(B\)能够构造出上述观察。

思考可以发现，当存在两段连续\(0\)的个数都大于等于\(2b\)时，\(B\)必然可以构造出这样一段，当然原来就有这么一段就不说了。

发现剩下的情况个数很少，我们直接分类讨论：

• 当不存在任何一个段长度大于等于\(2b\)时，显然此时所有合法段的长度都是不小于\(a\)的（前面的情况已经排除）。那么此时的胜负就根据合法段的奇偶个数。
• 当仅存在一个时，既然只有一段，直接枚举\(A\)在该段上的所有选择，看看存不存在必胜状态就行啦。\(A\)开始必然在这段区间上面选，不然\(B\)可以随便构造出满足“观察”的段。

代码如下：

Code

#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 3e5 + 5;

char s[N];
int a, b;

void A() {
    cout << "YES" << '\n';
}

void B() {
    cout << "NO" << '\n';
}

void run() {
    vector <int> v;
    cin >> a >> b;
    cin >> s + 1;
    int n = strlen(s + 1);
    int cnt = 0;
    for(int i = 1; i <= n; i++) {
        if(s[i] == '.') ++cnt;
        else {
            if(cnt) {
                v.push_back(cnt);
                cnt = 0;
            }
        }
    }
    if(cnt) v.push_back(cnt); cnt = 0;
    int f = 0;
    for(auto it : v) {
        if(it >= 2 * b) ++cnt;
        if(it >= b && it < a) f = 1;
    }
    if(f || cnt >= 2) {
        B(); return;
    }
    if(cnt == 0) {
        for(auto it : v) {
            if(it >= a) ++cnt;
        }
        if(cnt & 1) A();
        else B();
        return ;
    }
    int mx = *max_element(all(v));
    cnt = 0;
    for(auto it : v) {
        if(it != mx && it >= a) ++cnt;
    }
    for(int l = 1;  l + a - 1 <= mx; l++) {
        int r = l + a - 1;
        int left = l - 1, right = mx - r;
        if(left >= 2 * b || right >= 2 * b) continue;
        if((left >= b && left < a) || (right >= b && right < a)) continue;
        int tmp = cnt + (left >= a) + (right >= a);
        if(tmp % 2 == 0) {
            A(); return;
        }
    }
    B();
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

F. Choose a Square

题意：

二维平面上给出\(n\)个点，每个点都有个权值。现在要求选择一个正方形，满足其中一根对角线的两顶点在\(y=x\)这条直线上。

问所选正方形包含了的点的权值和减去边长的最大值。

类似于这样：



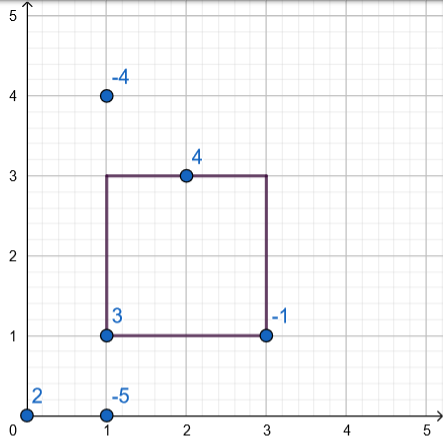
答案为\(4\)。

思路：

• 因为正方形具有对称性，所以我们可以考虑将\(y=x\)这条直线下方的点对称过去处理，那么我们现在就相当于选择一个等腰直角三角形的区域，类似于这样：

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAxcAAAIbCAIAAAAW9/SkAAAgAElEQVR4Ae3dX2xe530fcFEOrH+OvVCIKdBQEFl0wXSsnW1W0E2THLcDBSxtHBMFnBsFci868yoLICNALybmZkAg1bsJIHQXsWChmLUNro2iAcS1gD3PXlGrjZRJkDuJUyahgqTEjNlEteXZ4R751LRsU9T7nvec55znOZ8gkCnyPP8+v+Pgm/O+749Di4uLq/yHAAECBAgQIECgT4HVfV7vcgIECBAgQIAAgesCUpT7gAABAgQIECBQRkCKKqNmDAECBAgQIEBAinIPECBAgAABAgTKCEhRZdSMIUCAAAECBAhIUe4BAgQIECBAgEAZASmqjJoxBAgQIECAAAEpyj1AgAABAgQIECgjIEWVUTOGAAECBAgQICBFuQcIECBAgAABAmUEpKgyasYQIECAAAECBKQo9wABAgQIECBAoIyAFFVGzRgCBAgQIECAgBTlHiBAgAABAgQIlBGQosqoGUOAAAECBAgQkKLcAwQIECBAgACBMgJSVBk1YwgQIECAAAECUpR7gAABAgQIECBQRkCKKqNmDAECBAgQIEBAinIPECBAgAABAgTKCEhRZdSMIUCAAAECBAhIUe4BAgQIECBAgEAZASmqjJoxBAgQIECAAAEpyj1AgAABAgQIECgjIEWVUTOGAAECBAgQICBFuQcIECBAgAABAmUEpKgyasYQIECAAAECBKQo9wABAgQIECBAoIyAFFVGzRgCBAgQIECAgBTlHiBAgAABAgQIlBGQosqoGUOAAAECBAgQkKLcAwQIECBAgACBMgJSVBk1YwgQIECAAAECUpR7gAABAgQIECBQRkCKKqNmDAECBAgQIEBAinIPECBAgAABAgTKCEhRZdSMIUCAAAECBAhIUe4BAgQIECBAgEAZASmqjJoxBAgQIECAAAEpyj1AgAABAgQIECgjIEWVUTOGAAECBAgQICBFuQcIECBAgAABAmUEpKgyasYQIECAAAECBKQo9wABAgQIECBAoIyAFFVGzRgCBAgQIECAgBTlHiBAgAABAgQIlBGQosqoGUOAAAECBAgQkKLcAwQIECBAgACBMgJSVBk1YwgQIECAAAECUpR7gAABAgQIECBQRkCKKqNmDAECBAgQIEBAinIPECBAgAABAgTKCEhRZdSMIUCAAAECBAhIUe4BAgQIECBAgEAZASmqjJoxBAgQIECAAAEpyj1AgAABAgQIECgjIEWVUTOGAAECBAgQICBFuQcIECBAgAABAmUEpKgyasYQIECAAAECBKQo9wABAgQIECBAoIyAFFVGzRgCBAgQIECAgBTlHiBAgAABAgQIlBGQosqoGUOAAAECBAgQkKLcAwQIECBAgACBMgJSVBk1YwgQIECAAAECUpR7gAABAgQIECBQRkCKKqNmDAECBAgQIEBAinIPECBAgAABAgTKCEhRZdSMIUCAAAECBAhIUe4BAgQIECBAgEAZASmqjJoxBAgQIECAAAEpyj1AgAABAgQIECgjIEWVUTOGAAECBAgQICBFuQcIECBAgAABAmUEpKgyasYQIECAAAECBKQo9wABAgQIECBAoIyAFFVGzRgCBAgQIECAgBTlHiBAgAABAgQIlBGQosqoGUOAAAECBAgQkKLcAwQIECBAgACBMgJSVBk1YwgQIECAAAECUpR7gAABAgQIECBQRkCKKqNmDAECBAgQIEBAinIPECBAgAABAgTKCEhRZdSMIUCAAAECBAhIUe4BAgQIECBAgEAZASmqjJoxBAgQIECAAAEpqsl74MUXX3z++eeb3IG1CRAgQIAAgbICQ4uLi2XHGjeowMMPP/zmm2/+8Ic/HHQi4wkQIECAAIHoAp5FRSf/YMHwICr85/jx4x5HfUDinwQIECBAICUBz6Iaq1Z4EBVSVFj+i1/8osdRjZXBwgQIECBAoKyAZ1Fl5QYb9/5zqBeLOTyOGszSaAIECBAg0IyAZ1HNuC89iCqW9ziqmTJYlQABAgQIDCDgWdQAeGWH3vggqpjD46iylsYRIECAAIHGBDyLaoD+Yw+iih14HNVAJSxJgAABAgQGEJCiBsArO/THP/5xMXTLli3hi3PnzhV//fznP1984U8CBAgQIECg/QJSVJM1GhoaCstr2dVkDaxNgAABAgTKCnhfVFk54wgQINBtgRNnF46+drnbBk7fdQEpqut3gPMTIECghMBz//3i/iNn7lj3qRJjDSGQjYB/AbIppYMQIEAgkkCIUM+9fPHA9MSm4bWRlrQMgVYKSFGtLItNESBAoJUCv3jr3cOzF07MLYhQrayPTcUWkKJii1uPAAECiQqECHXwhXOX56+FCOW1vESLaNvVCviMXrWe/c3mM3r9ebmaAIHmBEKEOvDs2ZHhNbsnN4tQzdXByu0S8O7ydtXDbggQINBCgUvzbz/x1PEQoaYf2SJCtbBAttSUgGdRTclfX9ezqCb1rU2AQG8Cc397NXwcb/LBu6d2jvY2wlUEuiLgfVFdqbRzEiBAoIRAaAoVIlR4FW/XtpESww0hkLeAFJV3fZ2OAAEC5QWKjgbhVbztExvLz2IkgXwFpKh8a+tkBAgQGEAgRKjZY1d0NBiA0ND8BaSo/GvshAQIEOhLYKkp1MyecX01+6JzcdcEpKiuVdx5CRAgsJJA0dHg+p+aQq3k5GcErgv4jF6T94HP6DWpb20CBD4hoCnUJ0h8g8BKAvpFraTjZwQIEOiOQOhooClUd8rtpJUIeBZVCWPJSTyLKglnGAECVQtoClW1qPk6IeB9UZ0os0MSIEBgBYGiKZSOBisQ+RGBZQWkqGVZfJMAAQJdEdAUqiuVds4aBKSoGlBNSYAAgUQEnjl6/tVT85pCJVIu22ydgBTVupLYEAECBCIIhI/jHXzh3NzFq5pCRdC2RK4CUlSulXUuAgQI3FRAU6ib0vgBgX4EfEavH62qr/UZvapFzUeAwK0FNIW6tZErCPQmoF9Ub06uIkCAQBYCRVOoe0fXh0/k3bHOyxFZFNUhmhPwr1Bz9lYmQIBAXIEQofYdOr17cvOubSNxV7YagTwFpKg86+pUBAgQ+JjAKyffCG8n1xTqYyz+SmAQASlqED1jCRAgkIaAplBp1MkuUxOQolKrmP0SIECgTwFNofoEczmBXgWkqF6lXEeAAIHkBJaaQoW+mt5Lnlz5bLj9AjodNFkjnQ6a1Lc2gdwFio4G4ZR7vz4mQuVebedrRsCzqGbcrUqAAIFaBUKEmnn69a33bAifyBOhaqU2eZcF9IvqcvWdnQCBPAWKplD3b71TU6g8C+xUrRHwLKo1pbARAgQIVCFw4uzC/iNnNIWqwtIcBG4hIEXdAsiPCRAgkJCAplAJFctWMxCQojIooiMQIEDgukDRFOrJx+57YOwuIgQIRBCQoiIgW4IAAQK1C4S+5CfmFkJHg03Da2tfzAIECLwvIEW5EQgQIJC2QNEU6vL8NU2h0i6k3ScooF9Uk0XTL6pJfWsTyEKgaAq1Yd1tPo6XRT0dIjEBz6ISK5jtEiBAYEng0vzbB549qynUEogvCEQWkKIig1uOAAEC1QiEplD7Dp2e2jE6tXO0mhnNQoBAnwJSVJ9gLidAgEALBDSFakERbIHAKinKTUCAAIHEBI6+dvnw7IXwRqjtExsT27rtEshLwLvLm6ynd5c3qW9tAmkKhKZQs8euTH91i6ZQaRbQrrMS8Cwqq3I6DAECeQsUTaFm9oxrCpV3oZ0uFQEpKpVK2ScBAp0W0BSq0+V3+LYKeEWvycp4Ra9JfWsTSEegaAo1Mrwm/I7hO9b5f7/pVM5OcxdYnfsBnY8AAQJpC4SmUE88dVyESruKdp+pgP9Pk2lhHYsAgSwENIXKoowOka2AFJVtaR2MAIHUBTSFSr2C9p+9gBSVfYkdkACBJAVCR4PnXr6oKVSSxbPpzghIUZ0ptYMSIJCOQBGhDkxP6GiQTtHstIsCUlQXq+7MBAi0ViB8HC/0JT8xtyBCtbZGNkZgSUCKWqLwBQECBBoW0BSq4QJYnkCfAvpF9QlW6eX6RVXKaTICaQtoCpV2/ey+kwL6RXWy7A5NgEDLBEJHg6IpVHg7ub6aLSuO7RC4qYBnUTelifADz6IiIFuCQPsFQoTaf+TM5IN3T+0cbf9u7ZAAgSUB74taovAFAQIEGhDQFKoBdEsSqEhAiqoI0jQECBDoX0BTqP7NjCDQIgEpqkXFsBUCBDolECLU7LErOhp0qugOm5mAFJVZQR2HAIEEBIqOBnMXr87sGddXM4GC2SKBmwhIUTeB8W0CBAjUI1B0NLj+5/SEj+PVY2xWApEEfEYvEvSyy/iM3rIsvkkgYwFNoTIurqN1UEC/qA4W3ZEJEGhGQFOoZtytSqA2Aa/o1UZrYgIECNwgECLUvkOnd09u3rVt5IZv+5IAgYQFpKiEi2frBAikIlA0hQp9ybdPbExlz/ZJgMAtBaSoWxK5gAABAgMJaAo1EJ/BBFosIEW1uDi2RoBA+gLPHD3/6ql5TaHSr6QTEFhGQIpaBsW3CBAgMLjAUlMoHQ0GxzQDgXYKSFHtrItdESCQtoCmUGnXz+4J9CagX1RvTvVcpV9UPa5mJdCwgKZQDRfA8gRiCegXFUvaOgQIdEOgaAp17+j68Ik8rcm7UXOn7K6AV/S6W3snJ0CgcgFNoSonNSGBNgtIUW2ujr0RIJCSwCsn3zj4wjlNoVKqmb0SGExAihrMz2gCBAi8L6AplBuBQAcFpKgOFt2RCRCoWEBTqIpBTUcgEQEpKpFC2SYBAq0U0BSqlWWxKQKRBHQ6iAS97DI6HSzL4psEUhEoOhqE3e79+piP46VSNfskUKGAZ1EVYpqKAIEOCYQINfP061vv2bB7crMI1aHCOyqBGwT0i7oBw5cECBDoTaBoCnX/1js1heoNzFUE8hTwLCrPujoVAQL1CZw4u7D/yJnwCGrXtpH6VjEzAQLtF5Ci2l8jOyRAoEUCR1+7fHj2gqZQLSqJrRBoTkCKas7eygQIpCZQNIV68rH7Hhi7K7W92y8BAtULSFHVm5qRQDcFvvv9l/7kxdOrh4Ye/c1f/dY3duSHEPqSn5hbODA9sWl4bX6ncyICBEoISFEl0AwhQODjAiFC/fGfv75+eOuqVUN/9INT77z7y2//7kMfvyjZvxdNoS7PXwsRysfxki2jjROoXkC/qOpNe59Rv6jerfq78sTDq958sb8hrh5M4F/+4Xdv3/hPb7t9XZjmvXf+/p03fvg//s23B5uydaPfueff3T72ndZty4YIEGhOwLOo5uytXJ9AiFAPLdY3vZk/KbD6+3+4avXQB98fWvWpO/MowaX5tw88e1ZTqA8q658ECHxEQL+oj3D4CwEC5QS+8tD4z39y5r133goPov7uJ2d/+8tfKDdPq0aFplB7D578FxPDmkK1qi42Q6A9Ap5FtacWdkIgYYHiXVDh3eXhDF/7jfEM3hSlKVTCt6OtE4gl4H1RsaSXW8f7opZTqeJ7Lw3l8XJSFRbmKCNQdDTQFKqMnTEEuiTgWVSXqu2sBAj0IBAi1OyxK5pC9UDlEgJdF5Ciun4HOD8BAjcKFE2hZvaMawp1I4uvCRBYVkCKWpbFNwkQ6JyAplCdK7kDExhYQIoamNAEBAikLxAiVOhoMDK8ZvrxLfpqpl9PJyAQSUCng0jQliFAoLUCoSnUE08dDxFq9+RmEaq1ZbIxAi0U8CyqhUWxJQIE4gmEplD7Dp2e2jE6tXM03qpWIkAgCwEpKosyOgQBAqUENIUqxWYQAQL/ICBFuRUIEOiogKZQHS28YxOoTkCKqs7STAQIpCNQRKgD0xM6GqRTNDsl0DoBKap1JbEhAgRqFQgfxzs8e+HE3IIIVauzyQl0QUCK6kKVnZEAgX8QKDoaXP9zesLH8dwWBAgMKCBFDQhoOAECyQgsNYXaOzkmQiVTNhsl0GIB/aJaXBxbI0CgOoHQ0aBoChV+x7AIVZ2rmQh0WsCzqE6X3+EJdEQgRKj9R85oCtWRcjsmgWgCUlQ0agsRINCMQNEUKjyC2j6xsZkdWJUAgUwFpKhMC+tYBAi8L6AplBuBAIH6BKSo+mzNTIBAwwIhQs0eu6KjQcNlsDyBfAWkqHxr62QEOiwQPo538IVzcxevzuwZ11ezwzeCoxOoV0CKqtfX7AQIxBfQFCq+uRUJdFNAiupm3Z2aQLYCmkJlW1oHI9A+Af2i2lcTOyJAoKyAplBl5YwjQKCMgGdRZdSMIUCghQIhQu07dHr35OZd20ZauD1bIkAgPwEpKr+aOhGBLgpoCtXFqjszgaYFpKimK2B9AgQGFtAUamBCExAgUEZAiiqjZgwBAu0ReObo+VdPzWsK1Z6K2AmB7ghIUd2ptZMSyE1gqSlUiFB+wXBu1XUeAikISFEpVMkeCRD4hICmUJ8g8Q0CBGILSFGxxa1HgMDgAppCDW5oBgIEBhfQL2pwQzMQIBBVoGgKde/o+ulHtnghLyq9xQgQ+KiAZ1Ef9fA3AgTaLVB0NNAUqt1VsjsCXRGQorpSaecsIfDd77/0Jy+eXj009Ohv/uq3vrGjxAyGVCvwysk3wu8YDo+gtk9srHZmsxEgQKCEgBRVAs2QTgiECPXHf/76+uGtq1YN/dEPTr3z7i+//bsPdeLkbT2kplBtrYx9EeiugPdFdbf2Tr6yQHgKFSLUbbevv+32dXd+dmv468rX+2mtAqEp1OyxK6GjgadQtTqbnACBvgQ8i+qLy8UdEggv5K1aPfTBgZe++OAb/hlLoGgKdXn+mqZQscitQ4BArwKeRfUq5bquCXzlofGf/+TMe++89d47f/93Pzn721/+QtcE2nDeoqPB1bfem3l83Mfx2lAReyBA4EYBz6Ju1PA1gQ8FindBFS/kfe03xr0p6kOaWF+FCDXz9Otb79kQPpEnQsVStw4BAn0IDC0uLvZxuUsrFRgKrxmtWqUElaK+P9lLQ6secmNX7xpzxtAUat+h05MP3v2NXZ+Lua61CBAg0LuAZ1G9W7mSAIFIAppCRYK2DAECgwlIUYP5GU2AQNUCR1+7fHj2gqZQVbuajwCB6gWkqOpNzUiAQGmBoinUk4/d98DYXaUnMZAAAQJxBKSoOM5WIUDg1gKhL/mJuYXQ0WDT8NpbX+0KAgQINC0gRTVdAesTILBqlaZQ7gICBFIU0C8qxarZM4GsBIqmUOFImkJlVVeHIdABASmqA0V2RAItFrg0//begydHhteEt5NrCtXiQtkaAQLLCHhFbxkU3yJAII5A0RRqasfo1M7ROCtahQABAhUKSFEVYpqKAIE+BDSF6gPLpQQItFJAimplWWyKQO4CRUcDTaFyr7PzEchcQIrKvMCOR6CFAkWE+s6eL4TfkdfC7dkSAQIEehSQonqEchkBAhUIhI/jhb7kmkJVQGkKAgRaICBFtaAItkCgGwKaQnWjzk5JoEMCUlSHiu2oBBoUKJpCXe9o8LiOBg3WwdIECFQpoF9UlZrmIkBgWYHQFOqJp45rCrUsjm8SIJCugGdR6dbOzgmkIRCaQu0/ckZTqDSqZZcECPQjIEX1o+VaAgT6FNAUqk8wlxMgkJKAFJVSteyVQF8CP7967d9+90//6tT5L/3a5/7gya98esOavoYPfrGmUIMbmoEAgTYLeF9Um6tjbwQGEvjef/qLU+d+tvFz/+RHcz8LXw80V/+Diwh1YHpi+8TG/kcbQYAAgQQEpKgEimSLBMoJ/NlfnF131+bVqz8V/gxfl5ukxKiio8HssSshQm0aXltiBkMIECCQhIBX9JIok00SKClw2+3rSo4sO6zoaHD9z+mJO9b5X5iyjsYRIJCCgGdRKVTJHgmUEvjXO35l4dLf/PKX7761cOGhB7eWmqO/QUtNoWYeHxeh+rNzNQECCQpIUQkWzZYJ9Cbwe7/zpfvHht84/8N/vOUz39r9z3sbVP6q0NFAU6jyfEYSIJCgwNDi4mKC285ky0NDQ+EkSlB9OV8aWvWQG7t61xVmLJpCTT5499TO0RUu8yMCBAjkJOBdCzlV01kINCNQNIWafmSLj+M1UwCrEiDQkIAU1RC8ZQnkIqApVC6VdA4CBPoWkKL6JjOAAIElgWeOnn/11LyOBksgviBAoFMCUlSnyu2wBCoTKJpCzV28OrNnXFOoylhNRIBAUgJSVFLlslkC7RDQFKoddbALAgQaFpCiGi6A5QkkJ7DUFGrv5JimUMmVz4YJEKhQQL+oCjFNRSB/gaIp1L2j68Mn8kSo/OvthAQIrCjgWdSKPH5IgMANAiFC7Tt0evfk5l3bRm74ti8JECDQUQEpqqOFd2wC/QpoCtWvmOsJEMheQIrKvsQOSKACAU2hKkA0BQEC2QlIUdmV1IEIVC2gKVTVouYjQCATASkqk0I6BoE6BJaaQoW+mt5LXoewOQkQSFpAikq6fDZPoEYBTaFqxDU1AQJZCEhRWZTRIQhULRAi1MzTr2+9Z4OmUFXTmo8AgXwE9IvKp5ZOQqAqgaIp1P1b79QUqipS8xAgkKWAZ1FZltWhCJQXKDoaaApVXtBIAgQ6IyBFdabUDkqgB4FXTr5x8IVz4RHU9omNPVzuEgIECHRaQIrqdPkdnsCNAkVTqCcfu++Bsbtu/L6vCRAgQGBZASlqWRbfJNA5gfAI6sTcQuhosGl4becO78AECBAoJSBFlWIziEBGAkVTqMvz1zSFyqiqjkKAQAwBKSqGsjUItFagaAoVtjfz+Li+mq0tk40RINBOASmqnXWxKwIxBC7Nv33g2bOhKVT4RJ4IFUPcGgQI5CUgReVVT6ch0LNAaAq179DpqR2jUztHex7kQgIECBD4UECK+tDCVwS6I6ApVHdq7aQECNQnIEXVZ2tmAi0VOPra5cOzFzSFaml5bIsAgXQEpKh0amWnBKoQCE2hZo9d0RSqCktzECDQdQEpqut3gPN3SqBoCjWzZ1xTqE7V3WEJEKhJQIqqCda0BNoloClUu+phNwQIZCGwOotTOAQBAisJaAq1ko6fESBAoKyAFFVWzjgCiQiEplB7D54cGV4T3k6uKVQiRbNNAgTSEPCKXhp1sksC5QQ0hSrnZhQBAgR6EZCielFyDYEkBTSFSrJsNk2AQDoCUlQ6tbJTAv0IhI4Gz718UVOofsxcS4AAgf4EpKj+vFxNIAmBIkIdmJ7Q0SCJetkkAQKJCkhRiRbOtgksLxA+jhf6kp+YWxChlgfyXQIECFQnIEVVZ2kmAk0LaArVdAWsT4BAtwSkqG7V22kzFiiaQl3vaPC4jgYZ19nRCBBokYB+US0qhq0QKC0QmkI98dRxTaFKAxpIgACBEgKeRZVAM4RAuwRCU6j9R85M7Rid2jnarp3ZDQECBLIWkKKyLq/DdUBAU6gOFNkRCRBoqYAU1dLC2BaBXgQ0hepFyTUECBCoSUCKqgnWtARqFwgRavbYFR0Naoe2AAECBG4iIEXdBMa3CbRYYKkp1MyecX01W1woWyNAIHMBKSrzAjtefgJFR4Prf05P3LHOv8L5VdiJCBBIRsD/BCdTKhslEASWmkLtnRwTodwSBAgQaFZAv6hm/a1OoA+B0NFAU6g+vFxKgACBmgU8i6oZ2PQEKhLQFKoiSNMQIECgMgEpqjJKExGoT6BoCjX9yJbtExvrW8XMBAgQINCXgBTVF5eLCTQgoClUA+iWJECAQA8CUlQPSC4h0JzAM0fPv3pqXlOo5ipgZQIECNxUQIq6KY0fEGhWIHwc7+AL5+YuXtUUqtlCWJ0AAQI3E5Cibibj+wSaFNAUqkl9axMgQKA3ASmqNydXEYgooClURGxLESBAoLyAflHl7YwkUIdA0RTq3tH14RN5+mrWIWxOAgQIVCXgWVRVkuYhUIFAiFD7Dp3ePbl517aRCqYzBQECBAjUKSBF1alrbgL9CLxy8o3wdnJNofoxcy0BAgSaFJCimtS3NoElAU2hlih8QYAAgVQEpKhUKmWfOQtoCpVzdZ2NAIF8BaSofGvrZK0U+PnVa//xv/7lD17+32F3/+rXxx5/9MHD/+1iaAoV+mp6L3krK2ZTBAgQuKnA0OLi4k1/6Ac1CwwNDYUVlKB65peGVj3U0hv792ae+9Hcz9bdtTmc+hfz5//Rp9du//UH9359TISq/jYwIwECBGoW0OmgZmDTE/iowF/+r/N3fPZXPrVmQ/jvnSP3/eSnPxWhPirkbwQIEEhGQIpKplQ2mofAl37tcwuX/ubda1fDf39+5cwD45s9hcqjsk5BgEAHBaSoDhbdkZsU+IMnv7L9i5+7On/uvV/839/aMfa93/+tJndjbQIECBAYQMC7ywfAM5RA/wI/OveLn/6/4f/w+/9s+8TG/kcbQYAAAQItEpCiWlQMW8leoGgK9eRj9z0wdlf2h3VAAgQIZC8gRWVfYgdsi0DoS35ibiF0NNg0vLYte7IPAgQIEBhAQIoaAM9QAr0J/OKtd0OEujx/TVOo3sBcRYAAgTQEvLs8jTrZZboCIUIdePZs2P/M4+M+jpduHe2cAAECnxTwLOqTJr5DoDKBS/Nvhwi19Z4Nuyd1NKhM1UQECBBoiYAU1ZJC2EaGAnN/e3XfodNTO0ando5meDxHIkCAQOcFpKjO3wIA6hE4cXZh/5Ez4RHUrm0j9axgVgIECBBoWECKargAls9S4Ohrlw/PXph+ZIumUFnW16EIECBQCEhR7gQCFQuEplCzx65oClUxq+kIECDQPgEpqn01saOUBYqmUDN7xjWFSrmM9k6AAIGeBKSonphcROCWAppC3ZLIBQQIEMhMQIrKrKCO04xA0RRqZHjN9ONbNIVqpgZWJUCAQHQBXTejk1swO4HQFOqJp46HCKUpVHa1dSACBAisJOBZ1Eo6fkbglgKaQt2SyAUECBDIVUCKyrWyzhVDQFOoGMrWIECAQFsFpKi2Vsa+Wi8QOho89/JFTaFaXygbJECAQF0CUlRdsubNW6CIUL2a7AkAABIlSURBVAemJ3Q0yLvQTkeAAIEVBKSoFXD8iMAyAuHjeKEv+Ym5BRFqGR3fIkCAQJcEpKguVdtZBxbQFGpgQhMQIEAgHwEpKp9aOkndAppC1S1sfgIECKQloF9UWvWy28YEQkeDoilUeDu5vpqNlcHCBAgQaJOAZ1Ftqoa9tFUgRKj9R85M7Rid2jna1j3aFwECBAjEFpCiYotbLzkBTaGSK5kNEyBAII6AFBXH2SqpCmgKlWrl7JsAAQL1C0hR9RtbIVmBEKFmj13R0SDZAto4AQIE6hWQour1NXuiAkVHg7mLV2f2jOurmWgRbZsAAQJ1C0hRdQubPz2BoqPB9T+nJ3wcL7362TEBAgRiCUhRsaStk4jAUlOovZNjIlQiRbNNAgQINCOgX1Qz7lZtp4CmUO2si10RIECgnQKeRbWzLnbVgECIUPsOnd49uXnXtpEGlrckAQIECKQmIEWlVjH7rUegaAoV+pJvn9hYzwpmJUCAAIHcBKSo3CrqPCUENIUqgWYIAQIECEhR7oGuCzxz9Pyrp+Y1her6feD8BAgQ6F9AiurfzIhcBJaaQulokEtJnYMAAQJRBaSoqNwWa4+AplDtqYWdECBAIFEBKSrRwtn2QAKaQg3EZzABAgQIvC+gX5QboXMCRVOoe0fXh0/k6avZufI7MAECBKoT8CyqOkszpSCgKVQKVbJHAgQIpCEgRaVRJ7usROCVk28cfOGcplCVYJqEAAECBKQo90BXBDSF6kqlnZMAAQKxBKSoWNLWaVRAU6hG+S1OgACBPAWkqDzr6lRLAppCLVH4ggABAgSqFZCiqvU0W7sEio4GYU/6ararMHZDgACBLASkqCzK6BDLCYQINfP061vv2bB7crOOBssJ+R4BAgQIDCSgX9RAfAa3VqBoCnX/1js1hWptjWyMAAECqQsMLS4upn6GdPc/NDQUNq8ElVfw7Kk/nXl+JDyC2rVtpPLJTUiAAAECBAoBr+i5E3ITOPra5cOzI5pC5VZX5yFAgED7BKSo9tXEjgYQKJpCPfnYfQ+M3TXANIYSIECAAIFbC0hRtzZyRSoCoS/5ibmF8HG8TcNrU9mzfRIgQIBAugJSVLq1s/MPBYqmUJfnr+lo8CGKrwgQIECgZgHvLq8ZeMXpvbt8RZ5ef1g0hdqw7jYfx+uVzHUECBAgUIWAZ1FVKJqjOYFL828fePasplDNVcDKBAgQ6K6AFNXd2mdw8tAUat+h01M7Rqd2jmZwHEcgQIAAgbQEpKi06mW3HwqcOLuw/8gZTaE+FPEVAQIECMQVkKLielutIoGio4GmUBVxmoYAAQIEygh4d3kZtarGeHd5OckQoWaPXZn+6hZNocoBGkWAAAEClQh4FlUJo0niCRRNoWb2jGsKFQ/dSgQIECCwnIAUtZyK77VSQFOoVpbFpggQINBdAa/oNVl7r+j1rl80hRoZXhPeTn7HOum/dzlXEiBAgEBdAqvrmti8BKoTCE2hnnjquAhVnaiZCBAgQKACAf+fvgJEU9QqoClUrbwmJ0CAAIHSAlJUaToDYwhoChVD2RoECBAgUEpAiirFZlAUAU2hojBbhAABAgRKCkhRJeEMq1ugiFAHpid0NKib2vwECBAgUE5AiirnZlSNAuHjeIdnL5yYWxChalQ2NQECBAgMLCBFDUxogkoFio4G1/+cntDRoFJakxEgQIBAxQL6RVUM2td0+kV9jEtTqI+B+CsBAgQItFlAv6g2V6dbewsdDYqmUOF3DHsK1a3aOy0BAgTSFPAsqsm6eRa1pB8i1P4jZyYfvHtq5+jSN31BgAABAgTaLOB9UW2uTlf2VjSFCo+gtk9s7MqZnZMAAQIE0heQotKvYeIn0BQq8QLaPgECBLorIEV1t/ZtOHmIULPHruho0IZa2AMBAgQI9CsgRfUr5vpqBMLH8Q6+cG7u4tWZPeP6alZjahYCBAgQiCsgRcX1ttr7AppCuREIECBAIAMBn9Frsojd/IyeplBN3nPWJkCAAIHqBPSLqs7STD0IaArVA5JLCBAgQCANAa/opVGnPHYZItS+Q6d3T27etW0kjxM5BQECBAh0WUCK6nL1o55dU6io3BYjQIAAgfoFpKj6ja2wapWmUO4CAgQIEMhPQIrKr6atO9EzR8+/empeU6jWFcaGCBAgQGAwASlqMD+jVxRYagoVIpRfMLwilR8SIECAQHoCUlR6NUtlx5pCpVIp+yRAgACBcgL6RZVzq2ZUxv2iNIWq5hYxCwECBAi0WEC/qBYXJ9mtFU2h7h1dP/3IFi/kJVtGGydAgACBWwh4Re8WQH7cr0DR0UBTqH7dXE+AAAECyQlIUcmVrNUbfuXkG+F3DIdHUNsnNrZ6ozZHgAABAgQGFpCiBiY0wQcCmkJ9IOGfBAgQINAJASmqE2WOcEhNoSIgW4IAAQIEWiUgRbWqHElupmgKdXn+mqZQSdbPpgkQIECgrIBOB2XlqhiXQaeDoqNBwNj79TEfx6vipjAHAQIECCQj4FlUMqVq4UZDhJp5+vWt92wIn8gToVpYIFsiQIAAgVoF9IuqlTfnyYumUPdvvVNTqJzL7GwECBAgcHMBz6JubuMnNxfQFOrmNn5CgAABAl0RkKK6UukKz3n0tcuHZy9oClUhqakIECBAIEUBKSrFqjW556Ip1JOP3ffA2F1N7sPaBAgQIECgaQEpqukKJLV+6Et+Ym4hdDTYNLw2qY3bLAECBAgQqF5AiqreNMsZNYXKsqwORYAAAQKDCOgXNYjeoGNT6RdVNIXasO42H8cbtOTGEyBAgEBGAjodZFTMeo5yaf7tvQdPjgyvEaHqATYrAQIECKQq4BW9VCsXZ9+hKdS+Q6endoxO7RyNs6JVCBAgQIBAKgJSVCqVamCfmkI1gG5JAgQIEEhHQIpKp1Zxd1p0NNAUKq661QgQIEAgJQEpKqVqRdtrEaG+s+cL4XfkRVvUQgQIECBAIC0BKSqtetW+2/BxvNCXXFOo2qEtQIAAAQLpC0hR6dewuhNoClWdpZkIECBAIH8B/aKarHGr+kUVTaFCR4Pdk5vvWCdeN3ljWJsAAQIEkhDQLyqJMtW+ydAU6omnjmsKVTu0BQgQIEAgIwHPoposZkueRYWmUPuPnJl88G5NoZq8G6xNgAABAqkJeOEmtYpVvV9NoaoWNR8BAgQIdEVAiupKpZc9p6ZQy7L4JgECBAgQ6EVAiupFKc9righ1YHpi0/DaPE/oVAQIECBAoE4BKapO3bbOrSlUWytjXwQIECCQkoAUlVK1Ktlr0dHg+p/TEzoaVEJqEgIECBDopoDP6DVZ9/if0dMUqsl6W5sAAQIE8hLQLyqveq54mtDRQFOoFYX8kAABAgQI9CHgWVQfWJVfGvNZlKZQlZfPhAQIECDQcQHvi+rEDVA0hZp+ZMv2iY2dOLBDEiBAgACB+gWkqPqNm15BU6imK2B9AgQIEMhTQIrKs65Lp3rm6PlXT81rCrUE4gsCBAgQIFCVgBRVlWTr5gkfxzv4wrm5i1dn9ozrq9m68tgQAQIECKQvIEWlX8PlTqAp1HIqvkeAAAECBKoU8Bm9KjX7naumz+hpCtVvIVxPgAABAgRKCOgXVQKt1UOKplD3jq4Pn8jTmrzVpbI5AgQIEEhcwCt6iRfwo9sPEWrfodO7Jzfv2jby0Z/4GwECBAgQIFCxgBRVMWiD02kK1SC+pQkQIECggwJSVCZF1xQqk0I6BgECBAikIyBFpVOrm+9UU6ib2/gJAQIECBCoS0CKqks2zrxLTaFCX03vJY9jbhUCBAgQIFAISFEJ3wmaQiVcPFsnQIAAgfQF9ItqsoaD9IsKEWrm6de33rMhfCLPU6gmq2htAgQIEOiqgH5RSVa+aAp1/9Y7NYVKsn42TYAAAQJZCHhFL70yFh0NNIVKr3J2TIAAAQJ5CUhRidXzlZNvhN8xHB5BbZ/YmNjWbZcAAQIECOQlIEWlVM+iKdSTj933wNhdKe3bXgkQIECAQI4CUlQyVQ2PoE7MLYSOBpuG1yazaRslQIAAAQL5CkhRCdS2aAp1ef6aplAJVMsWCRAgQKAzAjodNFnqXjodFE2hwi73fn1MR4Mmq2VtAgQIECDwUQHPoj7q0bK/XZp/+8CzZzWFallZbIcAAQIECFwXkKLaex+EplD7Dp2e2jE6tXO0vbu0MwIECBAg0FUBKaqlldcUqqWFsS0CBAgQIPCBgBT1gUSb/nn0tcuHZy9oCtWmmtgLAQIECBD4uIB3l39cJObfl313eWgKNXvsyvRXt2gKFbMW1iJAgAABAv0KeBbVr1i91xdNoWb2jGsKVS+02QkQIECAwMACfhvxwIQVTRA6Gux/9kx4R7m+mhWJmoYAAQIdFXjzzTcffvjh559/vqPnj3hsr+hFxP7EUkuv6BVNoTasuy28F0pTqE84+QYBAgQI9CEQUtRnPvOZMODLX/7yN7/5za997Wt9DHZpPwKeRfWjVc+1oSnU3oMnR4bXiFD1AJuVAAECHRV48cUXH330Uc+l6iu/Z1H12d565vAs6tOfve/+R/79hb/+L+f/+j/feoArCBAgQIBAKQHPpUqx3WKQZ1G3AKr1x4uLi987/Gf/539+X4Sq1dnkBAgQIECgDgHPoupQNScBAgQIEGhMYOl9UcUOPIWqrxI6HdRna2YCBAgQINCkgPxUt74UVbew+QkQIECAQGwB+SmOuFf04jhbhQABAgQIEMhNwLvLc6uo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchOQonKrqPMQIECAAAECcQSkqDjOViFAgAABAgRyE5Cicquo8xAgQIAAAQJxBKSoOM5WIUCAAAECBHITkKJyq6jzECBAgAABAnEEpKg4zlYhQIAAAQIEchP4/0mSVF9YWeFRAAAAAElFTkSuQmCC" alt="">

• 注意到最终三角形的边上一定存在至少一个点，那么也就是说有用的横纵坐标就为这些点的坐标。
• 直接枚举\(x,y\)显然复杂度不能承受，考虑当我们枚举\(x\)时，选择一个最大的\(y\)，就类似于维护一个区间最大值。
• 对于一个位置\(x=x_0\)，显然随着\(y\)增大包含的点越多，并且对于一个\(y=y_0\)而言，与\(y=x\)这条直线所形成的三角形区域是必选的。类似于这样：

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAr8AAAHgCAIAAAAjS5IGAAAABmJLR0QA/wD/AP+gvaeTAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAgAElEQVR4nO3dbXBV930n8CODzaOhltdgi+IWS7S4IbY3wdmuHfzQB2WaTkPMdtd+saS4+2Q1L7rdxZOZ7WxNdqczm4G6b9Kq7c7GrplOYNsK00zSRUlbLK1ItqIJSuXFDbrBhdVFiEi2mnsjYV/MvjiOqmIQ9/zPuc+fzyvb4ugeJUj3q9/5/7//titXrkQAAGW7qdY3AAA0GOkBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkmnm9HDs2LGXX3651ncBAM2m7cqVK7W+h0p5/PHH33zzzW984xu1vhEAaCpNO3s4duzYsWPHTp48afwAANlq2tnD448/fuzYsSiKHnjgAeMHAMhQc84e4sFD/M/GDwCQreacPcwPHmLGDwCQoSacPSwcPMSMHwAgQ004e7hq8BAzfgCArDRhenj99dfjf9i0aVMURWfOnIn/9Yd/+IdrdEcA0FSaMD3Ma2tri6Koib9AAKiJJlz3ANAERsZmjg5fqPVdwLVJDwB1p28gv+/Q6dUrltb6RuDa/NUEqC99A/m+wfz+nq13ti+v9b3AtUkPAPWiMFs60H9uJDcjOlDnpAeAulCYLfUeOXNh+tL+nq2eWVDn7LkAqL3CbGn/wbH17ct2dW8UHah/Vk0C1NjE9Nwzz59c376sZ8cm0YGGYPYAUEu58eK+Q6e7t63b+UhHre8FyiXkAtTMyNjMvkOnd3Vv/MiD62t9L5CA9ABQG/HOzJ4dmx7eenut7wWSkR4AaqBvIN9/YtLOTBqU9ABQVfOlDnt3bxEdaFDSA0D1xDszC7MlpQ40NHsuAKpEqQNNQ98DQDXkxotKHWgaZg8AFafUgSYj/wJUVlzqYGcmzUR6AKggpQ40JekBoFJeOnr2+KvTSh1oPtIDQPbi47Zz+aJSB5qS9ACQMaUOND17LgCypNSBVqDvASAzcanDPR0rlTrQ3PzlBshGbrz43IunHLdNK5AeADIwNDrVe+SMnZm0COkBIC2lDrQa6QEgFaUOtCDpASDQfKmDnZm0Gjs2AULEOzOjKNrzVJfoQKvxNx4gscJsae8Lr3VuWKXUgdak7wEgmbjU4b7ONUodaFn+3gMkEB+3rdSBFic9AJRLqQPEpAeAssSlDs8+ufn+rrW1vheoMekB4MZ6j5wZyc0odYCY9ACwmLjU4cL0JaUOME/fA8B1xaUOq1Yssb0CFvLNAHBtE9Nz+w+OKXWA9/L9AHAN8XHbO7d37Hyko9b3AnVHegC4mlIHWJz0APAPHB2+cKD/nFIHWIRVkwB/r28g339isudjm5Q6wCLMHgDeFZc67N29RakDLE56AFDqAMl4cgG0urjUYX37MjszoUxO6AZa2sT03DPPnxQdIBHfKkDrUuoAYaQHoEUpdYBg0gPQiuLjtpU6QBjpAWg5cXRw3DYEkx6AFlKYLR3oPzeSmxEdIA3pAWgVSh0gK/oegJag1AEypO8BaH658WJc6tCzY5PoAOmZPQBNLjde3HfodPe2dUodICsyONDMlDpAJUgPQNNS6gAVIj0AzalvIN9/YtLOTKgE6QFoNvHOzFy+uHf3FtEBKkF6AJpKvDOzMFtS6gCVY88F0DyUOkB16HsAmoRSB6ga32BAM8iNF5978ZSdmVAd0gPQ8OJSBzszoWqkB6CxKXWA6pMegAb20tGzx1+dVuoAVSY9AA1pvtTBzkyoPt9yQONR6gC1pe8BaDBKHaDm9D0AjSQudbinY6VSB6gh33tAw1DqAHVCegAaw9DoVO+RM3ZmQj2QHoAGoNQB6or0ANQ7pQ5Qb6QHoH4pdYD6ZMcmUKfinZlRFO15qkt0gLriGxKoR4XZ0t4XXuvcsEqpA9QhfQ9A3YlLHe7rXKPUAeqTb0ugvsTHbSt1gHomPQB15OjwhQP95+zMhDonPQD1Ii51ePbJzfd3ra31vQCLkR6gMXzmc6984dipm9ranvjJH/uVT2yv9e1kr/fImZHcjFIHaAjSAzSAz3zulcN/9trK9s4oavuDL736VumdT/3io7W+qczEpQ4Xpi8pdYBGoe+B5EYej948VuubaC0f/t3P3HL7B5bcsiKKostvfe+tqW/873/3qVrfVMbe2vBrt3R9utZ3AZRFzCe5N49Fj8pkVXXT5343uqnt+//WFi1d0xz/F0xMz+0/OKbUARqOvgdoAD/76JbvXjx9+a3Zy2997+8ujv3cY/fW+o4ykBsv7ukdfWhru1IHaDi+Y6EBxKscvnDsVBRFH/+JLU2w6EGpAzQ06x5I7pW25hibUyuO24ZGZ/YAVFXfQL7/xKRSB2ho0gNQPXGpw97dW5Q6QEOTHoBqUOoAzcT3MFBxhdnS/oNj69uX9TxtewU0Azs2gcqamJ575vmT69uXKXWApuE7Gaig3HjxuRdP7dzesfORjlrfC5AZ6QGoFKUO0KykB6AilDpAE5MegOzF0cFx29CspAcgS4XZ0oH+cyO5GdEBmpj0AGQm3plZmC0pdYDm5tsbyMZ8qcOe7i7RAZqbvgcgA7nxYlzq4LhtaAW+yYG0cuPFfYdOK3WA1iE9AKnEpQ52ZkJL8eSC2puYnhsanar1XRCibyAvOkALMnsgxPSvfSDDz/Ynb/9MFEX33vynGX7OMv3fy5ujKPqxJaeDP8PFK+2vv/ODDy75ZnY3VQ3FKyv+6O2P/sItfxx2+a1P/97Nm7b1DeT7T0zamQktyOyBGiteWXHs7R9/dOn/qcmr//5bO1N+hj9866N/+86GTG6mfK+U/kmce4L9aemxNJfPXrq87+Dp/hOTe3dvER2gBZk9EK79v3w9/Sc5NTr1I8MXf/TpryS9sG8g3/3gujTL+4dGp9YOnP/wLz0Z/Bly48W/6h098KsfXL3i18u/qjBb6hvIf+Ijd4e9aGG29MfPn3z2yc3tXWvDPsPE9NxA7+j+nq3t7b8adgP7D44VZi8pdYCWZfZAjR0eOP/TD96R9KqRsZn+E5Mp37oO9J/b1b0xzWfoG8w/sf2upLfRPzz57fz3wl90IN/Vsfr+0OgQRdHhwfPd29aFzQzmSx32Pr1FdICWJT1QS7nxYi5fvL8z8Rvh4cHzD72vPc1LD41OrV6+NM178MjYzEhuJukexcJsKc4cYS9amC0dHjyfJvTEa1TDtlYqdQBi0gO1NDQ6FfC7+8T0XMDb9lXSDx7i3+ADBg9pJgd9A/mHtrZ3blgVdnkURQf6zwXcdhRFufHicy+e2tW9sWfHpuBXB5qD9EDNFGZL/Scmux9cl/TC/uHJgMyxUCaDh7F8ofqDh/4Tkzu3h8emsHlJfOFzL57q2bHpIw+uD351oGlID9TMSG6mq2N10qfvwZljocYdPDy89faUg4dd3RuT3rZSB+Aq0gM1E7Zesm8gf3/n2jS7BBt08DAxPdd/YjL48iiK4kqupMODl46ejUsdRAdgnvRAbYStl3x38LCtxoOHA/3ndm7vqPLgoX94MnijRBRFhdlS0i+8MFvad/D08Ven9UEBV5EeqI2w9ZLxw440Y4NMBg8Tb8wlfXSSyeAhzULR/uHJO29bXv4XHu/MvDCt1AG4BumBxK6UlkRR1Lb81uDPELx2Iexhx0INOngIW2YxL2l2UeoALE56oAbC1ksOjU4V5kppnr437uAhuKEhlqhgKi51uKdjpVIH4HqkB2ogbITw5eGLadYMRhkNHgL2LAyNTqUZPAQ3NMTiSU+ZX3i8M3NX98bgIm2gFUgPVNv8esnPfO6VD3/idx75hd/9zZcGy7lqJDdT28HD0OjUxBtzSe8hbocMzj258eLx0emUg4cy93kOjU7FOzOVOgCLM5ak2uL1kr/1+aHDf/bayvbOKGr7gy+9+lbpnU/94qOLXBVvVkwzSD88kKrgef4zBAweEi1XvErYURrz4uWWv/MfHrjxCw3k+wbzSh2Acpg9UFXz6yW/cOzUyvbOJbesXHLLijV3dH7h2KnFrxoanUrTEBVXHTTc4CG4GnJemU89lDoAiZg9UFXz6yVvamuLbmr7/n9uW+yaLBqiGnTwELa/Y14cPhYfPBRmS71HztiZCSRi9kBVza+X/NlHt3z34unLb81efut7f3dx7Oceu/d6l6Q/3CGTwUNhrpR0NUD6wUPA/o6Fbhg+4p2ZxdnLdmYCifh5QfUs7JeMVznEDyw+/hNbFln0EG9YSHO4QyaDh4AQkH7wEDDtWPjqi4ePwmxp7wuvdW5YleZVgNbkRwaJBbdFXdUv+alffHTxlZKxw4Pnez4WfiR0bQcPwXcetsxiocUftcTHbXdvW2dnJhDAkwuqJKxfMv17/+GB8088kqoloiaDh7BlFvOODl+Irn8gllIHICWzB6okrF8y7J17Xhw+UrZERMnPpUw/eAh40TJf/ejwhQP95+zMBNKQHqiSgBlAbryYfnqfweAh+WdIP3hIc9t9A/nrvXpc6vDsk5vTjHMAPLmgGsLO4+4bzKdpaM5q8FDljoeUt71IL3XvkTNxqYPoAKQkPVANAedxT0zPpSxKymTwELBZI83goTBbSnkYxzV7qQuzpX0HT+fGi/t7tqapzQCISQ9UXNh6yf7hyXoYPCQNAekHD2keecS91Fe9elzqEEWRUgcgK9IDFRewXjJ+D67tioewGUDKwUOa5BFF0eHB893b1i38n3piem5P7+j69mWO2wYyJD1QcQHnccfV1MENUZkMHgIO5Ez59t8/PJlm8JAbLw6NTi181pMbL+7pHe3etk50ALIlPZDYlbeXlP+Hw9ZLHn91OtWv4I05eIiP0wy4NtZ75MzCZz3zpQ5p1o4AXJP0QKCbVpTVNRmwXjLs9/6Fl0fpBg9Hhy+EhYA0g4e+gXxXx+o0X/XEG3PzQaFvIL/v0OmeHZuCSyMAFiE9UEHxesmkb+QpJwcpLw9++pB+xUOarRYLuynjUodP775XHxRQIR6FUkHxeslEyxfigyWTPumYl8mKh7AQcKD/XHC5ZN9A/qGt7SnXeXzkwfXxhs+R3IydmUBFmT1QQQHrJeNdA8FL/Bp08JDmCPL5iojCbKn3yBmlDkAVSA9USsB6yYnpubF8IXiVX/rBQ/CuhwP959KseHhvv1P54nvu3LBq/8Gx1SuWKnUAqkB6oFIC1kumbIhKP3gI2/WQZpnnNfudyhcPHh594PZnnj+p1AGoGumBighYLxlWSTkvk8FD2K6HNN3ScWAKftDQN5Dv2rDq0F+M79ze0bMjcNUFQFLSAxURsF4y3rIY/D7auIOH4Cc1hdnSF7964dzF2Se236XUAagmQ04q4svDFxOtl4wHD88+uTns5WoyePhu8dK//8wXv/3GrRt/4NJ3i5tvXbUs6YumXCL63AuvXSpdfvapzXZmAlVm9kBiV0pLoihqW37dtqjceHEkN5NovWQ8qwjuSqrJ4OGzn//a3+RLS25Z8a3XL3z2819L+qIT03NXFUsn8vv/6+yrZ/7u+V96v+gAVJ/0QPYC1ksG7O1c+HJRusFDWM/jV742tnzNXW1R24q1G7/ytbGkL3qg/1zY4CHemXlk6PyOD991T0fgTg2ANKQHMhawXnJkbKYwVwp++08/eAjb9dB28+q2trawF82NF4+PTgcMHuLjtnPjxU8/vSVNNyVAGtY9kLGA9ZKHB88/9L72sJcbGp1KkzyiFAdMrGnfcH787MrbNszOnPvow53JXnQwn3Q8E30/OqxvX7anu8vOTKCGzB7IWNL1khPTcyO5meDH/4cHwg+milIcMDE0OvVDd635sbuXT539xvs23fYru/5p+deOjM0EfMm58aJSB6BO+BlEluL1knue6ir/kv7hyYDfwmPx4CHNMZJ9A/n7O9cG9DzGp1rc33VfwIse6D+3c3tHoi85N17cd+j0zu0ddmYC9cDsgSwlXS+ZsiGqhoOH4I6H+BiwRF/yyNjMcy+e2tW9UXQA6oT0QGYC1kvGv/qHNUTVdvAQvGIxvrb8gNU3kN936HTPjk12ZgL1Q3ogM0nXS747eNhWs8FD/4nJKg8ehkanJt6YKz8HvHT0bP+Jyf09W0UHoK5Y90Bmkq6XTNMQVcPBw+GBkIcdC68tZ/Dw7nHb+eLe3Vsctw3UG7MHEnvnWl2TAf2SaRqiMhk87NyeeBlB3EwVnHiiKCon8cQ7My9MX9rfs1V0AOqQ2QPZSLpeMk1PQ20HD8HNVGVeq9QBqH9mD2QgYL3kl4cvBg8Pajt4CE485Vwblzrc07FSqQNQz6QHMpB0vWT8mKOGg4eHt95ezcFDYbZUzjaN3Hgx3pn5iY/cHfAqAFUjPZCBpOsl43Mlwn63zmTwEPAZUg4e7rxt+eKrJeJSh54dm9IEI4DqkB5IK+l6ycJsaWh0KqwhKqvBQ8BSxDSDh8ODN0g8Sh2AxiI9kFbS9ZJpGqIacfDQPzy5+OBBqQPQcKQHUkm6XjJ4xWKU0eChe9u6Kg8e4uM0r/fRfQdPH3912s5MoLFID6SSdL3k0OhU0vO756UcPExMz4WdqZFm8LDI8d8LSx1srwAai/RAYlcWtEUlXS95wxUA15N+8NA/PFn9wcP1TuEqzJb2vvDa+vZle5/eIjoADUd6IFzS9ZJpihobdPBwzU6quNThvs41Sh2ABiU9EC7pesngBJB+8HB48Hz1Bw/XPIVr/rhtpQ5A45IeCFQsLU20XjI3Xkx0vORC6QcPQ6NTOx+parnkNTuphkan4p2ZSh2AhiY9EGh0pj3R+se+wXz3tnUBg/qsBg8BL51y8HBV4ukbyPceOfPsk5vtzAQanfRAoD+fvKv89ZIT03MjuZmA3/6jhh08XPWgpPfImbjUIWzZB0BdkR4I9HMdZ8tfLxnvdwgbPAQ/74hVf/Bw1QrNuNQhN15U6gA0DemBQFvXvlHmW3K8cTF4xcOu7o3BGxNqMnhYuEIzLnUozl62MxNoJtIDFXe9jYs3lH7wcKD/XPUHD/N5ZWJ6Li512PNUl+gANBPpgYo7/up02MKF9IOHsMUW8TrNsNQyn1dy48U9vaMPbW1X6gA0H+mBxBZ2Td7Q0OjU6uVLA5YK1njwEBR3cuPF46PTOx/pmC91CFsoClDnpAcqK/gRQMrBw/wbedIL02wQjQ/EUuoAND3pgQoaGZuZeGOu/K0Z89IPHuI38moOHqIo2rm94+alNx0ePK/UAWhu0gMVlGa3ZMMNHqIo6j8x+crId/bu3qLUAWhuFnNRKRPTc2P5wp6nupJe2IiDh8JsqffIGcdtAy3C7IFKCW6ISjl4GBmbSbPVImDwEJc6RFGk1AFoEdIDFREf9BB2InYtyyWTDx4mpuf29I6ub19mZybQOqQHKqJvIN/VsTrsROyUg4exfKFqg4e41KF72zrRAWgp0gPZu+YJk+XIZPCwc3tHdQYPSh2AluW3JbI3kpvp6lgdsO8gk8FD2DrNpIOHvoF832C+Z8cmOzOBFiQ9kFjcNRktu+65FWENUZmUS1Zn8BBHB2dmAi1LeiBjwYdEpB88TLwxF7ZOs/zBQ2G2dKD/3EhuRnQAWpn0QMa+PHzxofe1J72qIQYPSh0AYlZNkqXgYy1TDh7i8FHRwUNc6rB6xVKlDgDSA1nqH54MKHmMHzqk2moRGj7KHDxMTM898/xJpQ4AMemBzAQ3RB3oP5d+8BAQPsq8MDde3Pviazu3d/Ts2BR2hwBNRnoggd/6/Ncee/q/v/hXP3XNj/YN5O/vXJt0LWFtBw83vDAudXhi+11KHQDmSQ+U6/f/5OsvHzsdrdwYLb8ziqLRsQsLP/ru4GFbyOAhbLVjLHiLRzmDh76B/L5Dp3t2bAo+dROgKXmCS7kOfmlkLrp9+fJbb1q6LIqik39z/kMLPjo0OhXQEBW8zXJevHChEoOHvoF8/4lJOzMB3svsgXKdvzizfHV7FEWrou9FUXThu1cWfvTLwxd/+sE7kn7OTAYPAYOBxQcP8c7M/hOTe3dvER0A3svsgXLddcfaQnF6+ap333FvXfX3b6thjw+yGjyEXXi9wUO8M7MwW1LqAHA9Zg+U6xd2/OOb3n7j7bnvvnP57SiKPvi+DfMf+vLwxYB38fSDhyiKsh08xNFhffsypQ4Ai5AeKNdTP/PAv/yZe68Uz165dDGKoge/nx5y48WR3ExtBg/JT9OIrj94yI0XlToAlEN6IIF/8/MfeuXFf/vPtw4t/I99g/mAdYuZDB4y3GqRGy/uO3RaqQNAOaQHUinMlkZyM0lHCPU2eIhLHXZ1b1TqAFAO41lSCWuIqqvBQ3zcds+OTWkaqwBaitkD4eKGqJ3bk/2+nn7wEDdbB1z43sHDS0fPxqUOogNA+cweCBc3RHVuWJXoqvSDh9XLlyatpYreM3iISx1y+aJSB4CkpAcSu1JaEkVR2/Jbv3ryjaQbNTMZPPR8LGRh48LBg1IHgDT83CTc3qe3JL2kVoOHhWdxzZc67OnuEh0AAlj3QPWkHDwUZkvBKx7mDwGPSx3u6Vip1AEgmJ+eVE/6wcOdty1PM3jIjRfjnZnOzARIQ3qgStIPHg4Png9b8RCnlpHcTO+RM3ZmAqTnyQVVUtvBw6W33xEdALJi9kA11HbwsPGOFa+MfGd/z1Y7MwEyIT1QDYcHz6cZPPQPT5Y5ePhu8dLv/dFffmnwW1EU/dSPd/34B7Z86/8V7mxf9vwn32+NJEBW/Dyl4kbGZsbyhT1PdYVdXpgt9Q3mn31yczl/+D/u++I3c2+sWLsxiqK+Pz/956OlTT94+/OfVOoAkCU/Uqm4w4Pnu7etSzN46OpYXeaKh7/867P/6Ic+2NZ2UxRFa+78kcuXS//1X90rOgBky6pJEpvvmiznD8eDh+CzK+PBQ/mNlh96/90zE39TulQsXSq+89Zc+4q31t+2LOylAbge6YHKSjl46BvIlz94iKLoN5792YcfuLs4feZy4W8/tHnZZ599JOx1AViEiS4VlH7FQ/+JyTJXPMS+eabwnbfbf/M/fdDOTIDKkR6ooCoPHvoG8vH6yoBaCADK58kFlZJ+xUP/icnyVzz0HjnTf2Jyf89W0QGg0sweqJSqDR4Ks6XeI2cuTF9y3DZAdZg9UBHpBw+HB8+Xc5xmfNx2FEV7n94iOgBUh5+2VET6wcP9nWs7N6xa/I9NTM/tPzjWuWFVfPp22GsBkJTZA9nLZMXDDQcPufHint7Rh7a29+zYJDoAVJOfuWSvCoOHkbGZfYdO7+re+JEH14e9CgDBzB5I7J1FuyYzGTzs3L7Y5UeHL+w7dLpnxybRAaAmzB7IWKUHD30D+bhCys5MgFoxeyBLlR48xKUOe3dvER0AasjsgSylHzw8vPX2aw4elDoA1A+zBzJTuXLJuNRh9YqlSh0A6oH0QGYyGTzc2b78qv8+MT33zPMn17cvU+oAUCekB7JRocFDXOqwc3uHUgeA+uHHMdmoxOBBqQNAfTJ7IAO58WKawcPE9Nx7Bw99A3mlDgD1yeyBxK68py2qbzCfZvDQPzzZvW3dwsFD30C+bzC/v2fre5dBAFBzZg+klRsvHh+dTjl46H5wXfyv8c7M/hOTogNA3TJ7IK2+wfwT2+/KZPCg1AGgIZg9kEomg4f4cqUOAI1CeiCVlIOH+Z0aufFiXOpgZyZA/ZMeCJd+8DA0OrXzkY7ceHHfodNxqUO2dwhAJfglj3CZDB7i6KDUAaCBmD0Q6NuTpfSDh5uX3qTUAaDhmD0Q6OWvz6UZPBzoP3f3upWvjHzHzkyAhmP2QIjX3/nBr56+FDx4+Ha+OPjNqe/MXNq7e4voANBwzB5I7MrbS7709mNPPPwDYYOHwmzpP/+PU2tWLX3+k++3vQKgEZk9kNjrpY0nLt/38Q+tCbi2MFv69Ze+VZgr/cYviQ4AjUp6ILEvzv3kR2/+i9XLE//liUsdLs5c+mePdKy/bVkl7g2AKvDLH4k9tuz43aULUfTJRFflxovPvXhqV/fGO29b3rlhVYXuDYAqkB5I7H03f+udy7ckumRkbCbemfnw1tsrdFcAVI30QMXFx22LDgBNQ3qgsl46evb4q9NKHQCaifRApcTHbefyRcdtAzQZP9OpiPi47cJsSXQAaD5+rJO9ODqsb1+2p7tLdABoPvoeSOxKaUkURW3Lb73mR+NSh3s6Vvbs2CQ6ADQlP9zJ0nypgzMzAZqY9EBmhkaneo+csTMToOlJD2RDqQNA65AeyIBSB4CWIj2QilIHgBbkxz3h4p2ZURSJDgAtxU98AhVnS3s//1rnhlW7ujeKDgAtRd8DgX7lt//6vs41Sh0AWlDblStXan0PldLW1hZFURN/gbWS+8Yf/7cv3fHz3T+q1AGgNfmtkWSODl840P9DdmYCtDLpgQTiUodnn9x8f9faWt8LADUjPVCu3iNnRnIzSh0AkB64sbjU4cL0JTszAYismuSG4lKHVSuW2F4BQMybAYuZmJ7bf3BMqQMAC3k/4Lri47Z3bu/Y+UhHre8FgDoiPXBtI2Mz+w6d3tW9UakDAFeRHrgGx20DsAirJrla30C+/8Rkz8c2KXUA4JrMHvgH4lKHvbu3KHUA4HqkB96l1AGAMnlyQRR9v9RhffsyOzMBuCEndBNNTM898/xJ0QGAMnmraHVKHQBISnpoaUodAAggPbQupQ4AhJEeWlQcHRy3DUAA6aHlFGZLB/rPjeRmRAcAwkgPrSXemVmYLSl1ACCYvocWotQBgEzoe/iW5akAAAWNSURBVGgVufFiXOrQs2OT6ABAGmYPLSE3Xtx36HT3tnVKHQBIz++gzS8udbAzE4CsSA9NTqkDAJmTHppZ30C+/8SknZkAZEt6aE7xcdu5fHHv7i2iAwDZkh6akFIHACrKnotmo9QBgErT99BUlDoAUAXeYJpHbrz43IunHLcNQKVJD01CqQMAVSM9NAOlDgBUk/TQ8F46evb4q9NKHQCoGumhgc2XOtiZCUA1ectpVEodAKgVfQ8NSakDADWk76HxxKUO93SsVOoAQE1472kw8c5MpQ4A1JD00EiGRqd6j5yxMxOA2pIeGoZSBwDqhPTQGJQ6AFA/pId6F5c6XJi+ZGcmAHXCjs26Fu/MjKJoz1NdogMAdcIbUv0qzJb2vvBa54ZVSh0AqCv6HupUXOpwX+capQ4A1BtvS/VIqQMA9Ux6qDtHhy8c6D9nZyYAdUt6qC9xqcOzT26+v2ttre8FAK5NeqgjvUfOjORmlDoAUOekh7qg1AGABqLvofbiUodVK5bYXgFAQ7Bjs8Ympuf29I6ub18mOgDQKLxd1VJuvPjci6d2bu/Y+UhHre8FAMolPdSMUgcAGpT0UBuO2wagcUkPNRBHh0/vvrdzw6pa3wsAJCY9VFVhtnSg/5xSBwAamvRQPUodAGgO+h6qJC51WN++zHHbADQ6fQ/VMDE998zzJ5U6ANAczB4qLjde3HfodPe2dUodAGgOfg+uLKUOADQf6aGClDoA0JSkh0qJo4OdmQA0H+khe0odAGhu0kPG4p2ZhdmSUgcAmpU9F1lS6gBAK9D3kJnceFGpAwCtwOwhG0odAGgdfkXOQFzqYGcmAC1CekhLqQMArUZ6SOWlo2ePvzptZyYALUV6CBQft53LF/fu3iI6ANBSpIcQSh0AaGX2XCSm1AGAFqfvIZm41OGejpVKHQBoWd7/EsiNF5978ZTjtgFocdJDuZQ6AEBMeiiLUgcAmCc93JhSBwBYSHpYzHypg52ZADDPO+J1KXUAgGvS93BthdnS3hde69ywSqkDAFxF38M1xKUO93WuUeoAAO/lrfFq8c5MpQ4AcD3Swz8wNDrVe+SMnZkAsAjp4e/FpQ7PPrn5/q61tb4XAKhf0sO7eo+cGcnNKHUAgBuSHt4tdbgwfcnOTAAoR6vv2IxLHaIo2vNUl+gAAOVo6ffLiem5/QfHlDoAQCKt+5YZH7e9c3vHzkc6an0vANBIWjQ9KHUAgGCtmB6ODl840H9OqQMAhGm5VZN9A/n+E5M9H9uk1AEAwrTW7CEuddi7e4tSBwAI1iqnZBVmS/sOns6NF/VBAZDGm2+++fjjj7/88su1vpFaaoknF3Gpw6oVS5yZCUBKb7755m233RZF0WOPPfbLv/zLH//4x2t9RzXQ/LOHiem5Pb2j69uXiQ4AZOjYsWNPPPFEi84hrjSvKIpuvWPzw//6D+/+wL+o9f/MADSzxx577PDhw7V+36ueZp49XLly5bMHvvLtr37u7Nf/Z63vBQCaRzOvewCAzM2ve4i15uoH6wAAIERr5oaY9AAAybRyboh5cgEAJNPMqyYBgEqQHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACSkR4AgGSkBwAgGekBAEhGegAAkpEeAIBkpAcAIBnpAQBIRnoAAJKRHgCAZKQHACAZ6QEASEZ6AACS+f8ZRKlCRq6WxwAAAABJRU5ErkJggg==" alt="">

• 所以线段树的做法就很显然了，横坐标直接从后往前枚举，依次加点并且不断在线段树中插入点的信息并更新区间信息，查询的时候就直接查询最大值以及纵坐标即可。
• 为什么是更新区间最大值？
• 因为每插入一个点，它会影响在它右上方的点，当选择右上方的点时，它也必然被包含，类似于这样：（所以直接更新在其上方的区间信息即可）

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAyQAAAIDCAIAAAB6tk1pAAAABmJLR0QA/wD/AP+gvaeTAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAgAElEQVR4nO3df3Td5X0f8OfaEGMMdm019iJihpHcmUZFtLWTNMYmZI1MSBsHN6uddDCStAfE6TndFoPbQYezpDkYq3RnJ4vC1iYeJAc5pQK3DYlEFhyBaYKVFDEx01rXovYkbBHJKEiVTYTv/vjaF8U/ZEn3fu+v7+v1R465unr0PFIkvfW9n/u+qUwmEwAAiMesYm8AAKCSCVsAADEStgAAYiRsAQDESNgCAIiRsAUAECNhCwAgRsIWAECMhC0AgBgJWwAAMRK2AABiJGwBAMRI2AIAiJGwBQAQI2ELACBGwhYAQIyELQCAGAlbAAAxErYAAGIkbAEAxEjYAgCIkbAFABAjYQsAIEbCFgBAjIQtAIAYCVsAADEStgAAYiRsAQDESNgCAIiRsAUAECNhCwAgRsIWAECMhC0AgBgJWwAAMRK2AABiJGwBAMRI2AIAiJGwBQAQI2ELACBGwhYAQIyELQCAGAlbAAAxErYAAGIkbAEAxEjYAgCIkbAFABAjYQsAIEbCFgBAjIQtAIAYCVsAADEStgAAYiRsAQDESNgCAIiRsAUAECNhCwAgRsIWAECMhC0AgBgJWwAAMRK2AABiJGwBAMRI2AIAiJGwBQAQI2ELACBGwhYAQIyELQCAGAlbAAAxErYAAGIkbAEAxEjYAgCIkbAFABAjYQsAIEbCFgBAjIQtAIAYCVsAADEStgAAYiRsAQDESNgCAIiRsAUAECNhCwAgRsJW4uzevfvxxx8v9i4AIClSmUym2HugoK6//vrXXnvt7//+74u9EQBIBFe2kmX37t27d+9+/vnnXdwCgMJwZStZrr/++t27d4cQrrnmGhe3AKAAXNlKkOiyVvRvF7cAoDBc2UqQ7GWtiItbAFAArmwlxcTLWhEXtwCgAFzZSorTLmtFXNwCgLgJW0nx8ssvR/9YtmxZCKG3tzf6zyuuuKJIOwKARBC2EieVSoUQfN0BoDDMbAFQNrp6htv2Hin2LmB6hC0AykNrR//2nfsvmXtBsTcC0+P/sgCUgdaO/tan+5sa6/7FoouKvReYHmELgJI2Mjb+cPuhrvSwpEWZErYAKF0jY+PNu3qPDB1vaqzzACJlyrMRE8ezEYFyMTI23tTSs2TRnJsblkpalC8D8gCUosNDx25/4Pkli+Y0rl8maVHWXNlKHFe2gNKX7hvdvnN/w8rFG9ZWF3svkCt/KwBQWrp6hrfv3H9zw9J1q5YUey+QB8IWACUkqnhoXL9sdV1VsfcC+SFsAVAqWjv62zsHVDxQYYQtAIovW6a19dYVkhYVRtgCoMiiioeRsXFlWlQkz0ZMHM9GBEqKMi0qnp4tAIom3TeqTIuK58pW4riyBZQIZVokhD8jACiCqExLxQNJIGwBUGjKtEgUYQuAgnqo7eCzLw4p0yI5hC0ACmRkbLx5V2+6f1SZFokibAFQCMq0SCzPRkwcz0YECk+ZFkmmZwuAeEVlWldWX6xMi2Tyf3oAYpTuG713x76bG5auW7Wk2HuB4hC2AIjLnu7B5l29Kh5IOGELgFgo04KIsAVA/inTgixhC4B8ypZpqXiAiOqHxFH9AMQnqngIIWzeVCtpQcR3AgD5MTI2vvWrL9VcNk+ZFkykZwuAPIjKtK6uma9MC07j+wGAXHX1DG/fuV+ZFpyVsAVATpRpweSELQBmLirTunPj8vraBcXeC5QoYQuAGWre1duVHlamBZMTtgCYtqhM68jQcWVacF56thJHzxaQo6hMa97c2Z54CFPhmwSAaTg8dKyppUeZFkyd7xMApirdN3rvjn0b1lRvWFtd7L1A2RC2AJgSZVowM8IWAOfXtvfIw+2HlGnBDBiQTxwD8sB0tXb0t3cONH5kmTItmAFXtgCYTFSmtfXWFcq0YGaELQDOTpkW5IWHERPHw4jAVERlWksWzVHxADmaVewNAFByDg8du/2B5yUtyAvfQgD8DGVakF/CFgBvUaYFeSdsAXBSa0d/69P9yrQgv4QtAEI4lbSaGutUPEB+CVsASTcyNv5w+6Gu9LCkBXEQtgASTZkWxE3PVuLo2QKylGlBAejZAkiodN9oVKbVuH6ZpAXxcWUrcVzZAkII6b7R7Tv3N6xcrEwL4uZPGYDEUaYFhSRsASSLMi0oMGELIEFaO/rbOwdUPEAhCVsAiRBVPKT7R7feukLSgkIStgAqX1TxMDI2rkwLCs+zERPHsxEhaZRpQXHp2QKoZMq0oOh84wFUrHTf6L079ql4gOIStgAqU1SmpeIBik7YAqhAyrSgdAhbAJXmobaDz744pEwLSoSwBVA5smVaKh6gdPhWBKgQyrSgNOnZShw9W1CRlGlBydKzBVD2ojKtK6svVqYFJcj3JEB5U6YFJU7YAihje7oHm3f1qniAUiZsAZQrZVpQFoQtgLKkTAvKhbAFUGaUaUF5Uf2QOKofoKxFFQ8hhM2baiUtKAu+UQHKxsjY+NavvlRz2TxlWlBG9GwBlIeoTOvqmvnKtKC8+HYFKANdPcPbd+5XpgXlSNgCKHVte4883H5IxQOUKWELoKRFZVp3blxeX7ug2HsBZkLYAsrYtq98729275uVSt30r3/xP9yyptjbyb/mXb1d6WFlWlDWVD8kjuqHmAzduzJEn95UKhNSIaRSs1IhpELq1P+e+kcqlQohlUmlQkilUme5Qwip1KxZIYTMyfvPCiGcfOus6Ektb92eif6RSkW3p2bNyoRUSEV7OXl75uSC0eIhlZqVOfmxQip18vZMCKfuf/L2TPb+s2YNHLv4wOj89/z8QPb+qdTJI2R3Gx08lZoVffRTmzm58+ztmZ89USo1K5P6mROdXCfacHSO1IRDZW+fNetbz/zjD//vK2+btyQTUv/8+pF3/9I7P7x2xcSThp890bk+7QOvp9I/zvzalbOjL1lmwpfp1Kf9PCf955+mWp8b+bdr5//Mp/3kid76cmRSb50ouj0z4f6nnXT02IkH//afXhn66dZPrjAOD2VN2EocYSsOQ//5V4q9hXN6NbPo5RPvXDX7hVwWefSnHwohfOzCb5XCZvK4TiT30z360w+9/OY7N1/0P/Oyn4kuueU331b72bwvCxSSv5YgbxZ9tjOTyYRMJhUyIWQyJzIhZELm1P+e+kcmkwkhk8pkQshkMme5QwiZTObEwGtvHjhy/NeWX5TJnAghnHzriRMhhFPrnAjRH0yZE+Fkes5kTpxIhUzIhGiRkMn89XPjqRAuXZk6tXjIZE6kTn6skMmciG5PhXBqnUzIhHDq9hDCyLHM97556X0f/Mkl896bvX8mc/II0QeNPnjq5AcN2dtTp3Ye3f7MP1TNCmHu8l8LE25PZX7mRCfXOXEihEz0n5nMyUNld/jMPy0LJ0785OAbsy68dNasWSFkwonxzBuvr1u9/OQ7Rp+QCSeKdn7mp310/MLd/7j28zVPXnjhquhLlprwZTr50Sec6Kwn3X3o2t//+W/NnvMvs5/2EMJbpzj15Uhl3jpRdHtqwv2zJ81kMm++eSIVMrNmpSQtqADCFuRPatbJR/Oi/5p9jnud49+nefK5gyFctLrq8lx2NDI2/p2e55sa6y7MYeJnX/fg8iteXXptrhNRI2PjTz3zfFNj3dzcxo9GxsafeuD5psa6//X45Y9+Z9+lVbUhZH7yavrfNFy14beum+5qL3QP/kLq1Ss/2TTj/ezpHqzueOV9d/y3Ga8wUbpv9N4d+za8v3rD2uq8LAgUnVJTKEUjY+PtnQMNqxbnuE5Xeri2+pIcZ6sf63jlg6venuNO8rWZiets+dR1H/v1q94Y7nljOP3RD6zY8qlpJ62Qj9M91vHKTWvfkcsKWV09w/fu2Hdzw1JJCyqJK1tQivKVS3LPAem+0XT/aH1NHkoH8hVKJq6z5VPXzSxjRXI/Xbpv9PDRY3n5/EQVD8q0oPK4sgWlKC8Xk/KSk/Z0D9605h25PxsuX6Etj+Ev5ON0rU/3N6xcnPvnp7Wjv71z4M6NyyUtqDzCFpScfOWJ3JNEvh7NzMtm8rtOyMfpRsbGu9LDuX9+mnf1tncObL11hdpSqEjCFpScvOSJvOSkfD2ama/QlsfwF/JxutaO/vqaBbmsMDI2vr1lf7pvVG0pVDBhC0qL0fgCrBPJ8XQnv1Irc7ow1tTSc8ncC9SWQmUTtqC05HE0PseclN/R+LyEtnytE/JxuugrNeMH/g4PHbv9geeXLJpzc8NSSQsqm+9wKC15ecqe0fjzyv10uXylTpZprVGmBYngyhaUEKPxBVgn5ON0XT3Dh48em9kzB5VpQdIIW1BCjMbHvU4k99PNeFqrtaN/+879jeuXrVu1ZMYfHSgvwhaUCqPxBVgnkuPpDg8d60oPz+C6VFRb2tRYp0wLEkXYglJhNL4A64R8nK5978DquqppXYAcGRuPyrRUPEACCVtQKrTGx71OJMfTzaDxIap4UKYFiSVsQUkwGl+AdUJeRuPTw7XVl9RcNm/qH7GppWfJojnKtCCxhC0oCUbj414nkvvppnUBMt03GpVpNa5fJmlBYglbUHxG4wuwTiTH03X1DI8cG5/ieHu6b3T7zv0b1lQ3rl82448IVABhC4rPaHwB1gn5ON1jT7/yvnctmso9lWkBWcIWFJ/R+LjXieR4usNDx3r6R6YSnrJlWioegCBsQdEZjS/AOiEfp2vfO9CwcvF5N9Pa0R9VPEhaQETYgiIzGh/3OpEcTxdtZvL8NDI2vr1lf3vnwNZbV6h4ALKELSgmo/EFWCeS4+n2dA9O3vgQVTwcGTquTAs4jbAFxWQ0vgDrhHyc7sm9r9605h3neqsyLWASwhYUk9H4uNeJ5Hi6Pd2DI8fG62vPvhllWsDkhC0oGqPxBVgn5ON0T+599Vyvz5PuG40qHpRpAecibEHRGI2Pe51Ijqc7PHSsKz181s1EZVqN65etW7Uktz0ClUzYguIwGl+AdSI5nq5978BZM7EyLWCKhC0oDqPxBVgn5Hy6kbHxx55+5cxM/FDbQWVawBSZ5YTieKzjlZvWnvPZbVNkNP68cjxd+96B+poFEzPxyNh4867edP9oU2OdcXhgKlzZgiIotdH4vFyeKdnR+FxO1945MLHxYWKZlqQFTJGwBUWQx9H4HHNS9GjmJF2dhdxMHteJ5Hi6Pd2DIYRs44MyLWBmhC0otPyOxueYk/I7Gp97aMvXOpEcTzexyDQq07qy+mJlWsB0CVtQaEbjC7BOyPl06b7RrvRwdI0tqni4uWHpLesuz8vegETx9xkU2uSj8du+8r2/2b1vVip107/+xf9wy5pz3c1o/Hnl3hofvfue7sHmXb0qHoAZc2ULCmryPLHtK9977H+/9LYFNRfMr/n6Ey9u+8r3zrWO0fjJ5Xi67EO9rR39khaQI2ELCmryPPE3u/ddvKhm9tsunv22ufPfXvM3u/ed9W5G488rx9O1dvTXVl/SvndAmRaQO2ELCue8eWJWKhVmpU79V+pcd8tLTnpy76sVPBqf4+na9g4cH3/zhfRPmhrr8lVkDySWsAWFc9488eHrVrz+6v433xh7841//smrPb/5/qvOerfcc1I0/Z2X6ah8hbZ8rRNyPt3//uHA8TdOzLlgtooHIC+ELSic8+aJLZ+67mO/ftUbwz1vDKc/+oEVWz513Zn3yUtOyuNofF5CWx7DX8jtdCNj4198rLf2nfM2b6qVtIC88KMECiTKE5s31U5+ty2fuu6sGSsrX6Pxn7317JfNpqVkR+Nndrp03+i9O/Zdd03V7374CkkLyBdXtqBAtMbHvU5kxqfLlmn9+4+5pgXkk7AFhZCvPGE0/rxmdrq2vUe279zfuH7ZulVL8rINgCxhCwohX3nCaPzkZna61o7+h9sP3blxuYoHIA7CFhRCXvKE0fjzmsHpmnf1RmVa2RecBsgvYQtil688oTV+ctM93cjY+PaW/em+UWVaQKyELYid0fi414lM63QjY+NNLT0hBGVaQNyELYiX0fgCrBOZ+ukODx3b3Ny9ZNGcxvXLJC0gbsIWxMtofAHWCdM5XbpvdHNzd8PKxZIWUBjCFsTLaHzc60SmeLpsmdaGtdV5+bgA5yVsQYyMxhdgnTDl07V29CvTAgpP2IIYGY2Pe53IVE7X2tHf+nT/Z2+9SpkWUGDCFsTFaHwB1olMfrqRsfFsmVa+PiLA1AlbEBej8QVYJ5zvdFHSUqYFFJGwBXExGh/3OpFJTheVaV0y9wJlWkARJTFs3XHHHffff3/el73hhhs2bdo0ODiY95UpR0bjC7BOmPR0h4eO3f7A88q0gKJLXNgaHBw8cODAli1bVq1adVowOnDgwCTv+MQTT7S0tJx244MPPtjS0pJdZ9GiRVVVZm8JwWh8/OtEznW6dN/o1h0vbVhT3bh+WV4+EMCMJS5sVVVVffvb3/7yl7/c2dn5nve8p6urK/umpqam2traMxNV5G//9m8//vGPT3zr4ODg7bff3tHRkQ1YV1xxRZx7p2wYjS/AOpGzni4q07ppzTuUaQGlIKGX1m+77bZ3vetdH/nIR66//vqnnnqqvr4+hNDe3h5C+OAHP3jWd/nSl74UQrjjjjuuuuqq6P4/+MEPQgj19fXPPPNMCGFwcPDll1+O/h259NJLo3uSNKU2Gr95U22OO5n6Zl4fPf7vt33zhy8efPcvXf6nd3740nlzZrbOVJz1dFHFQ+P6ZSoegBKRuCtbWddee+1TTz0VQtiyZUsIoaurK51O33nnnZM8Dvi5z32upqbmt37rt6LHDR966KEQwu23375mzZo1a9Z0dnY2NzevmSBamQRK8mj8Fx/5/ou9R6su/+UX0ke/+Mj3Z7zOVJx5uihpNTXWSVpA6Uhc2Lr77ruzU1b19fVf+9rXtm3bFkJ48MEHQwgf+9jHJnnfqqqqP//zP48CWVdX186dOx955JHMKevWrdu2bVtmgq9//euFORQlJeGj8d/5fs/cBUtnzbpg7oKl3/l+z4zXOa/TTjexTEvFA1BSEhG2Jk6+79y5c8eOHdnLVzfeeGN9ff3g4GBLS8vGjRvPO95eX19/2223DQ4O/u7v/u7ChQvP9ZhjxLB8MhmNn/22uXlZZ3ITTxdVPCjTAkpT5c9sHThwoKamprGxMRq6qq2t/cAHPnDafZ588smjR4/+/u///hTXHB4e/sxnPnPw4MF9+/ZlbzxzZisY20qeKE989tarclynfEfjb1zzCy1t/zB/yfKx4UM3rq6Z8TrnlT1dlLSWLJqzuaFWxQNQglKZTKbYe4jXE0888eEPf/ib3/zmjTfeGEK44YYbPvCBD9x1110T71NbW1tbW/vtb3/7rCt0dXW9/vrr2f+srq5+9NFHpziPtW7dunMtWyypVCqEUPFf9wIb+s+/Ev1j75tXf++n79l80f/MccGmY7933YU/WDX7hVwW+b9vLv+Xs/7fvNRYKWwmj+tEsqfrSy195lf+q4oHoGRV/sOIe/bsWbhwYZS0zur+++9Pp9P33HNPCOHuu+9etWrVaXfYsmXLxLH3Rx999NOf/vTE2azstNbTTz8dQpjx2FZrR//Wr77UtvfIyNj4jM5K8X3vp++57sIf5L7OjRfu/sVZ+3Nc5Bdn7889aeVrM3lcJ5I93YJLLpS0gFJW+Zfcd+7c2dDQcK63Hjhw4L777mtsbLz22mtDCAsWLOjs7Lz//vsnXvr6+te/np2+ii4LnTaMNUlr/LTGtjasrZ43d/bfdR9taulZXVd1ZfXFDasWG0ApI4v+y4829gzXXPZ7uT+YdW1eNpQn+dpMfg/V1TO8fed+FQ9A6avwK1tRocNHP/rRs751cHBw48aNixYt+tznPhfdctddd61cufK+++6bOFN/3sDU2dm5YEF+nsq+btWSrZ9c8eSfrv7gqrcfOXq88YGuzV/qfqjtYLpvNC/rE7f62gXGhgqgtaNf0gLKRYX/VvjGN74Rzt1T+sd//MednZ3PP//8xDj1Z3/2Z2vWrGlqaooG6s8rimXvfe97z3zT4ODgjJ+QuLquKvotsqd7MN03eu+OfaNjbzasWvy+dy2qr81PsIMy9VDbwWdfHPLEQ6BcVPKVrcHBwebm5nMVOtxxxx3Nzc2PPPLIac8WvPbaaxsbG5ubmyd/qcSs5557buHChWd9yuHv/M7v5P6K16vrqm5Zd/nX7l659dYV8y6a3fzXvR/8zJ7tLfv3dHvFaxJnZGx8e8v+Z18c2nrrCkkLKBeVHLb+4i/+4ujRo7fccstptw8PD2eT1qZNm858x9tuuy169/N+iMHBwXvuuecP//APz/qmtra2l19+eSZbP5v62gW3rLv8y//xmsc+/56a6nmPdbzywc/siQbq8/UhoJRFFQ9Hho67pgWUl0p+GPGuu+563/veF02+T/SFL3whhHCupBVCqK+vb2xs/O3f/u3J1z9w4MDGjRtDCJ/+9Kcn3n733XcvWLDgu9/9bgjhE5/4xIz3fy6XzL1gw9rq6BV2Wzv6swP1V9fMf1/dIr+EqEjKtIDyVeE/s05LWk888cRzzz1XU1PzV3/1V2c+8HfHHXesXbs2SmDnHdh68MEH/+iP/iiE8NRTT2UfprzqqqvWrVsXhbmamppHHnnkzKiXX9nUtad78NnuoeZdvfU1C66umb+6ripf1ZFQdNHYYsPKxbesu7zYewGYtsovNY0888wzn//859va2kII27ZtO63UNHLDDTe0tbWd6xMyODj46KOP3n777evWrfvSl770+uuvb9myZdu2baVWEL+ne/CF9E/a9w7Mmzt7dV3VmQP1Sk3jEJWaLvovPyr2RipQlLRubli6btWSYu8FYCYq/MpWCKGlpWXHjh1tbW3RpaYdO3ac9W7RiFX0sOCZ7r///vvuu+/d7373tm3bXn755ej1f0owaYVTT2NsXL+sq2e4Kz3c/Ne96b7RDWurPY2RcqRMC6gAlRy2BgcHly9ffvTo0ShmRY8P7tix47777gsh1NXVzZ8/P4Tw4osvDg8P/+Vf/mUI4awvj/jEE09s2bJl4ozXJz7xic9//vPXXHNNTU1NQ0PDFVdccfnll7/zne8MITz77LPZd4zGtn71V3/1T/7kT2I/7RnqaxdEM/WHh4492z30cPuhzc3dq+uq3vGuD73y4rcKvx+YrtaO/tan+yUtoNxV+MOIXV1dfX19E1+rp6ura8uWLdHjiVnr1q37uZ/7uVtuueVcr+rT0tJy5jR9V1fXN77xjR/+8IfPPffc0aNHz3yvlStXVlVV3XPPPXFPbk1da0f/F77YunDpL0cD9Q2rFps1zgsPI+ZdVKal4gGoABUetjhTNLP1zP/58bPdQ+17B6KBeq8LlCNhK49Gxsabd/Wm+0ebGuv8MQBUAGErcU4bkM8O1C9ZNKe+ZoHRrpkRtvIlqngYGRvf+skVkhZQGYStxDnXsxGjgfr2zgGvCzQDwlZejIyNb/3qSzWXzbu5YamkBVQMYStxzlv9kO4b7UoPP9s91JUeXl1X9Wt1Cz3l/ryErdwp0wIqlbCVOFPv2RoZG2/fO5BNXQbqJyFs5SiqeFCmBVQkYStxZlZqGjXUt+8dWF1XdWX1xQbqTyNs5WJP92Dzrl4VD0ClErYSJ8cG+exAfU31vJrL5jWsXOx1gYKwlYOoTOvOjcvNCAKVSthKnHy9XM+e7sF036iB+oiwNTPNu3q70sPKtIDKJmwlTt5fG7GrZzjdP9reOZDuG21Ytfh9dYsS+GCQsDVdUZnWkaHjKh6AiidsJU58L0R92kB9op7GKGxNS1SmFULYvKlW0gIqnrCVOPGFrYna9h75u+6je7oHEzJQL2xN3eGhY00tPcq0gOQQthKnMGErK3oa47PdQzXV866umb+6rqoiB+qFrSmKyrQ2rKnesLa62HsBKBB/VhKv1XVV0QhXNFB/7459BuoTS5kWkEyubCVOga9snSl6XaBnXxxK941uWFsdXe4q1mbyxZWt82rbe+Th9kPKtIAEErYSp+hhK6uSBuqFrcm1dvS3dw40fmSZy5lAAglbiVM6YWuiiQP15fi6QMLWJJRpAQknbCVOaYatrOzrAtXXLCijgXph66yUaQEEYSuBSjxsZUWvC7SnezCEsLquqsQH6oWtM0VlWvPmzm5cv0zSApJM2EqccglbWdmB+iNDx0v2aYzC1mkODx3buuOl+poFyrQAhK3EKbuwlXV46FhU2VWCA/XC1kTKtAAmErYSp3zD1kStHf3Z1FUKA/XCVpYyLYDTCFuJUxlhK+u0gfpivS6QsBVp7ehvfbpfmRbARMJW4lRY2MqKBurb9w7UVM+ruWxegUe7hK1wKmk1NdapeACYSNhKnEoNW1nRQH1750AhXxco4WFrZGz84fZDyrQAzkrYSpyKD1tZ6b7RrvRwNNrVsGrx1TXz45siSnLYUqYFMDlhK3GSE7ayznxdoNV1VeeKBSNj43u6B6cbyxIbtqIyrSWL5qh4ADgXPxypfJfMvWDD2pM1BNFAfVNLz+q6qiurLz5zoH5P92BTS08IwZPpzuvw0LHNzd2r66oa1y8r9l4ASpewRbKsrqtaXVd156bl0UB94wNd0UB9w8rF0esC/V330RCCvHVe6b7R7Tv3K9MCOC8PIyZOAh9GnNye7sF032h2oL5978DI2Hj0psb1y6aSJP77I9//+L47Qgh/dfWXf+9j7453u6VBmRbA1LmyRdJF17puWXd5V89we+dbSSuE0LyrN4Qwed76X3/9o8d37//4khBC+Nq39l06722bPnRNzFsuMmVaANMyq9gbgFJRX7tgdOzN025s3tX7UNvBSd6r5YmuY+FktcSJCxZ+5fEKn5Fv7ehv7xxoaqyTtACmSNiCk0bGxnv6RybecsncC2oum3eg/58PDx0713u98urwRZcsiv590byFAz/+Sby7LJ6o4qG9c0CZFsC0eBgRTkr3jf6LhRetrqtasnBOTVl6wjAAAAu9SURBVPW8JYvmTCVSvOPtC0ZGh8K8EEI4Nnp08c/Pj32jxRBVPIyMjTc11ql4AJgWPzThpPraBTPomv9363+5+dGu6N+zxo/+zvoKHNjKlmltbqiVtACmy89NyMmmD13z+ugb4YUQQvjtX/9X/+4jv1LsHeVZum/03h37lGkBzJjqh8RR/RCHSm2Qj8q0GlYuVqYFMGOubAFnF5VpqXgAyJGwBZyFMi2AfBG2gNM91Hbw2ReHmhrrVDwA5E7YAt4SlWml+0eVaQHki7AFnKRMCyAOfp4CISjTAoiNl+sBQrpv9PYHnr+y+uLG9cskLYD88lMVki6qLb25Yem6VUuKvReACiRsQaLt6R5s3tWr4gEgPsIWJJcyLYACELYgoZRpARSGsAWV7/XR4//j0eeeePofQwi//t7aT9608uEn+9P9oyoeAArAz1mofJ/Z/s0X0kfnLlgaQmj97v7v7j20+r0rJS2AwlD9AJXvuf9z8JK3/8IFc+ZdMGfe/CXLX/3xjzdvUqYFUCDCFlS+d//S5cOH/2H8+Oj48dHXB/bXr1gqaQEUjLAFle9P7/zw6msuHx3qfXPkn35jTe0X/9NvFHtHAAnir1uofC/0jvz4p4v+7D/9qooHgMITtqDCRWVad25cXl+7oNh7AUgiYQsqWfOu3q70sDItgCIStqAyjYyNN+/qPTJ0XMUDQHEZkIcKNDI23tTSE0LY+skVkhZAcfkpDJXm8NCxppaemsvm3dyg4gGg+PwghoqS7hu9d8e+DWuqN6ytLvZeAAhB2IJK0tUzvH3n/psblq5btaTYewHgJGELKkTb3iMPtx9qXL9MmRZASRG2oBK0dvS3dw4o0wIoQcIWlL2oTGvrrSuUaQGUIGELypgyLYDS56czlKuoTGvJojmNn1wmaQGULKWmUJYODx27/YHnlyyao0wLoMT5GQ3lR5kWQBkRtqDMKNMCKC/CFpST1o7+1qf7lWkBlBFhC8pGlLSaGutUPACUEWELysDI2PjD7Ye60sOSFkDZEbag1CnTAihrfnBDSVOmBVDu9GxB6Ur3jUZlWo3rJS2AcuXHN5SodN/o9p37lWkBlDthC0qRMi2AiiFsQclRpgVQSYQtKC2tHf3tnQMqHgAqhrAFpSKqeEj3j269dYWkBVAxhC0oCVHFw8jYuDItgArjZzoUX7ZMa3NDraQFUGH0bEGRKdMCqGx+skMxpftG792xT8UDQAUTtqBoojItFQ8AlU3YguJQpgWQEMIWFMFDbQeffXFImRZAEghbUFDZMi0VDwAJ4Wc9FI4yLYAE8uMeCkSZFkAy6dmCQojKtK6svliZFkDS+KEPsVOmBZBkwhbEa0/3YPOuXhUPAIklbEGMlGkBIGxBXJRpARCELYiDMi0AsvwagDyLKh5CCJIWAEHYgvwaGRvf+tWXai6bd3PDUkkLgKBnC/Liwl+49sKqn0RlWlfXzFemBUBWKpPJFHsPFFQqlQoh+LrnXc+L39z6+BJlWgCcxh/fkAdte4883L5ExQMAZxK2IFdRmdadG5fX1y4o9l4AKDnCFuSkeVdvV3pYmRYA5yJswQxFZVpHho6reABgEgbkE8eAfF5EZVrz5s72xEMAJueXBEzb4aFjTS09yrQAmAq/J2B60n2j9+7Yt2FN9Ya11cXeCwBlQNiCaejqGd6+c78yLQCmTtiCqYoqHpRpATAtBuQTx4D8zLR29Ld3DjR+ZJkyLQCmxZUtOL+oTGvrrSuUaQEwXcIWTEaZFgA58jBi4ngYceqiMq0li+aoeABgxmYVewNQog4PHbv9geclLQBy5FcInIUyLQDyRdiC0ynTAiCPhC34Gcq0AMgvYQveEiWtpsY6FQ8A5IuwBSGEMDI2/nD7oa70sKQFQH4JW3Cy4mFkbFyZFgB5p2crcfRsnUaZFgCx0rNFoqX7RqMyrcb1yyQtAOLgylbiuLKVle4b3b5zf8PKxcq0AIiPP+VJqKhMS8UDAHETtkgiZVoAFIywReK0dvS3dw6oeACgMIQtEmRkbLx5V2+6f3TrrSskLQAKQ9giKZRpAVAUno2YOMl8NqIyLQCKRc8WlU+ZFgBF5BcPFS7dN3rvjn03Nyxdt2pJsfcCQBIJW1QyZVoAFJ2wRcVSpgVAKRC2qEwPtR189sUhZVoAFJ2wRaXJlmmpeACgFPhVREVRpgVAqdGzlTgV3LOlTAuAEqRniwoRlWldWX2xMi0ASorfSVSCqOJBmRYAJUjYouzt6R5s3tWr4gGA0iRsUd6UaQFQ4oQtypgyLQBKn7BFWYrKtI4MHVfxAECJU/2QOBVQ/RBVPIQQNm+qlbQAKHF+UVFmRsbGt371pZrL5inTAqAs6NminERlWlfXzFemBUC58OuKsqFMC4ByJGxRHtr2Hnm4/ZCKBwDKjrBFGYjKtO7cuLy+dkGx9wIA0yNsUeqad/V2pYeVaQFQpoQtSpcyLQAqgJ6txCmXnq2oTGve3NmeeAhAWVP9QCk6PHRsc3P3kkVzJC0Ayp1fY5ScdN/ovTv2bVhTvWFtdbH3AgC5ErYoLcq0AKgwwhYlJKp4UKYFQCURtigVUdL67K1X1Vw2r9h7AYC8EbYovpGx8YfbDynTAqAiCVsUmTItACqbnq3EKamerahMa8miOTc3LJW0AKhIerYomsNDx25/4HllWgBUNle2EqdErmyl+0a379zfsHKxMi0AKpvLCRSBMi0AkkPYotCUaQGQKMIWBRUlLRUPACSHsEWBKNMCIJmELQohqngYGRtXpgVA0ng2YuIU/tmIyrQASDI9W8Qr3TeqTAuAJHNlK3EKeWVLmRYAuNJAXKIyLRUPACScsEUslGkBQETYIv8eajv47ItDKh4AIAhb5NfI2Hjzrt50/+jWW1dIWgAQhC3ySJkWAJzJsxETJ6ZnIyrTAoCz0rNFHkRlWldWX6xMCwBO4/ciuUr3jd67Y9/NDUvXrVpS7L0AQMkRtsiJMi0AmJywxcwp0wKA8xK2mCFlWgAwFcIW05Yt01LxAADn5Tcl06NMCwCmRc9W4uTSszUyNr71qy/VXDZPmRYATJGeLaYqKtO6uma+Mi0AmDq/MpmSqOJBmRYATJewxfnt6R5s3tWr4gEAZkDY4jyiMq07Ny6vr11Q7L0AQPkRtphM867ervSwMi0AmDFhi7OLyrSODB1X8QAAuVD9kDhTqX6IyrRCCJs31UpaAJALv0c53eGhY00tPcq0ACAv/CrlZ6T7Ru/dsW/DmuoNa6uLvRcAqATCFm9RpgUAeSdscVLb3iMPtx9SpgUA+WVAPnHOOiDf2tHf3jnQ+JFlyrQAIL9c2eJkmdbWW1co0wKAvPNC1Ik2Mja+vWV/um9UbSkAuXjttdeuv/76xx9/vNgbKUUeRkyc7MOIUZnWvLmzG9cvU/EAQC5ee+21hQsXhhDe//73/8Ef/MFHP/rRYu+ohLiylVCHh45tbu5esmiOpAVAHu3evfumm25ylWsiV7YSJ5VKXfr25Vev/8KhH/3lwR99o9jbAaBiucoVcWUrcTKZzBcf/s6Bv/uKpAUABeDKFgCQq+zMVsQ1rYkM6wAAeSNmnUnYAgDyQMw6Fw8jAgDEyIA8AECMhC0AgBgJWwAAMRK2AABiJGwBAMRI2AIAiJGwBQAQI2ELACBGwhYAQIyELQCAGAlbAAAxErYAAGIkbAEAxEjYAgCIkbAFABAjYQsAIEbCFgBAjIQtAIAYCVsAADEStgAAYiRsAQDESNgCAIiRsAUAECNhCwAgRsIWAECMhC0AgBgJWwAAMRK2AABiJGwBAMRI2AIAiJGwBQAQI2ELACBGwhYAQIyELQCAGAlbAAAxErYAAGIkbAEAxEjYAgCIkbAFABAjYQsAIEbCFgBAjIQtAIAYCVsAADEStgAAYiRsAQDESNgCAIiRsAUAECNhCwAgRsIWAECMhC0AgBgJWwAAMRK2AABiJGwBAMRI2AIAiJGwBQAQI2ELACBGwhYAQIyELQCAGAlbAAAxErYAAGL0/wFZ+OfrrHDmVQAAAABJRU5ErkJggg==" alt="">

• 注意一个细节，因为最后还要减去正方形的边长，对于一个点\((x,y)\)而言，正方形边长就为\(y-x\)，减去就是加上\(x-y\)。因为我们是按照\(y\)值建立线段树的，初始答案就为\(-y\)，最后加上枚举的\(x\)就行了。

最后还要注意特判一下答案为负的情况，可能答案不包含任何点。

详见代码：

Code

#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
const int N = 5e5 + 5;

int n;
vector <int> v;
pll tr[N << 2];
ll add[N << 2];

struct node{
    int x, y, c;
    bool operator < (const node &A) const{
        return x < A.x;
    }
}p[N];

void push_up(int o) {
    tr[o] = max(tr[o << 1], tr[o << 1|1]);
}

void push_down(int o, int l, int r) {
    if(add[o]) {
        tr[o << 1].fi += add[o];
        tr[o << 1|1].fi += add[o];
        add[o << 1] += add[o];
        add[o << 1|1] += add[o];
        add[o] = 0;
    }
}

void build(int o, int l, int r) {
    add[o] = 0;
    if(l == r) {
        tr[o] = MP(-v[l], v[l]);
        return;
    }
    int mid = (l + r) >> 1;
    build(o << 1, l, mid); build(o << 1|1, mid + 1, r);
    push_up(o);
}

void update(int o, int l, int r, int x, int c) {
    if(x <= v[l]) {
        tr[o].fi += c;
        add[o] += c;
        return;
    }
    push_down(o, l, r);
    int mid = (l + r) >> 1;
    if(x <= v[mid]) update(o << 1, l, mid, x, c);
    update(o << 1|1, mid + 1, r, x, c);
    push_up(o);
}

pll query(int o, int l, int r, int L) {
    if(L > v[r]) return MP(-1000000009, 0);
    if(L <= v[l]) return tr[o];
    push_down(o, l, r);
    int mid = (l + r) >> 1;
    pll ret = max(query(o << 1, l, mid, L), query(o << 1|1, mid + 1, r, L));
    return ret;
}

void run() {
    v.clear();
    for(int i = 1; i <= n; i++) {
        int x, y, c; cin >> x >> y >> c;
        if(x > y) swap(x, y);
        p[i] = {x, y, c};
        v.push_back(y);
    }
    sort(all(v));
    v.erase(unique(all(v)), v.end());
    build(1, 0, sz(v) - 1);
    sort(p + 1, p + n + 1);
    p[0].x = -1;
    pll ans = MP(-1000000009, 0);
    int ansx;
    for(int i = n; i >= 1; i--) {
        update(1, 0, sz(v) - 1, p[i].y, p[i].c);
        if(p[i - 1].x != p[i].x) {
            pll ret = query(1, 0, sz(v) - 1, p[i].x);
            ret.fi += p[i].x;
            if(ret > ans) {
                ans = ret;
                ansx = p[i].x;
            }
        }
    }
    if(ans.fi < 0) {
        ans = MP(0, 1000000001), ansx = 1000000001;
    }
    cout << ans.fi << ' ' << ansx << ' ' << ansx << ' ' << ans.se << ' ' << ans.se << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    while(cin >> n) run();
    return 0;
}