BZOJ4259：残缺的字符串（FFT与字符串匹配）

很久很久以前，在你刚刚学习字符串匹配的时候，有两个仅包含小写字母的字符串A和B，其中A串长度为m，B串长度为n。可当你现在再次碰到这两个串时，这两个串已经老化了，每个串都有不同程度的残缺。

你想对这两个串重新进行匹配，其中A为模板串，那么现在问题来了，请回答，对于B的每一个位置i，从这个位置开始连续m个字符形成的子串是否可能与A串完全匹配?

Input

第一行包含两个正整数m,n(1<=m<=n<=300000)，分别表示A串和B串的长度。

第二行为一个长度为m的字符串A。

第三行为一个长度为n的字符串B。

两个串均仅由小写字母和*号组成，其中*号表示相应位置已经残缺。

Output

第一行包含一个整数k，表示B串中可以完全匹配A串的位置个数。

若k>0，则第二行输出k个正整数，从小到大依次输出每个可以匹配的开头位置（下标从1开始）。

 

Sample Input

3 7
a*b
aebr*ob

Sample Output

2
1 5

https://www.cnblogs.com/clrs97/p/4814499.html
假设字符串是从第0位开始的，那么对于两个长度都为n的字符串A,B，定义距离函数
dis(A,B)=∑i=0n−(A[i]−B[i])[A[i]!=′∗′][B[i]!=′∗′]
dis(A,B)=∑i=0n−(A[i]−B[i])[A[i]!=′∗′][B[i]!=′∗′]
若把*号都设置为0，那么有
dis(A,B)=∑i=0n−(A[i]−B[i])2A[i]B[i]
dis(A,B)=∑i=0n−(A[i]−B[i])2A[i]B[i]
如果dis(A,B)=0dis(A,B)=，那么A和B完全匹配。

对于这个问题，假设我们枚举B的末尾位置i，设f[i]=dis(A,B[i−m+,i])f[i]=dis(A,B[i−m+,i])，那么B的这一个子串与A完全匹配，有

f[i]=∑j=0m−(A[j]−B[i−m++j])2A[j]B[i−m++j]=
f[i]=∑j=0m−(A[j]−B[i−m++j])2A[j]B[i−m++j]=
如果把A串翻转，并在后面不断补0直至和B串等长的话，那么有

f[i]===∑j=0i(A[j]−B[i−j])2A[j]B[i−j]∑j=0i(A[j]−2A[j]B[i−j]+B[i−j])A[j]B[i−j]∑j=0iA[j]3B[i−j]−∑j=0iA[j]2B[i−j]+∑j=0iA[j]B[i−j]
f[i]=∑j=0i(A[j]−B[i−j])2A[j]B[i−j]=∑j=0i(A[j]−2A[j]B[i−j]+B[i−j])A[j]B[i−j]=∑j=0iA[j]3B[i−j]−∑j=0iA[j]2B[i−j]+∑j=0iA[j]B[i−j]
显然可以分成三段做FFT求出所有的f[i]，时间复杂度为O(nlogn)O(nlog⁡n)。

思路大意就是用乘法表示一段字符串，如果为0，表示匹配。(A[i]-B[i])^2中的平方的原因是为了避免正负抵消为0。

首先需要会使用 FFT，卷积。卷积是指一个倒序，一个正序（序号之和相同）的乘积。

   

   

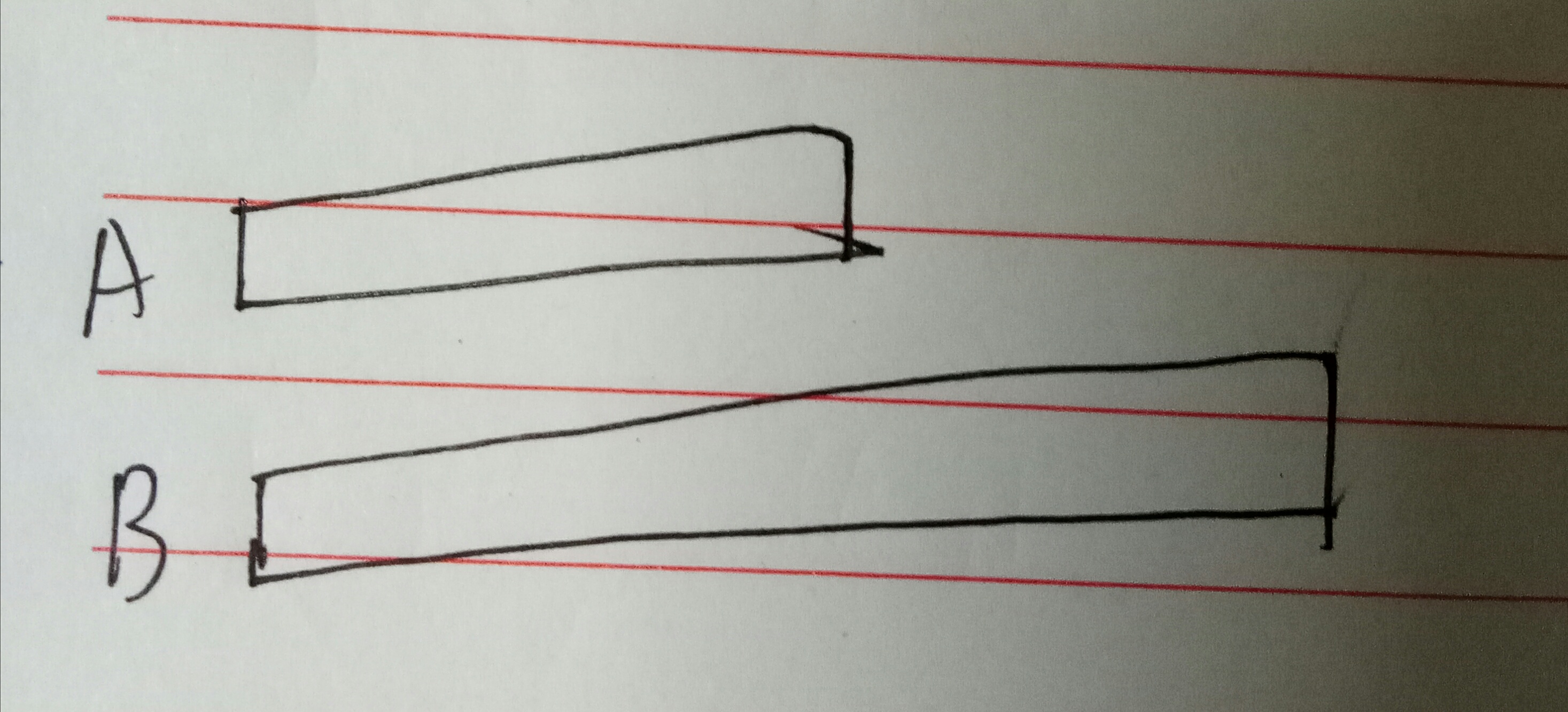
图一：A字符串和B字符串。

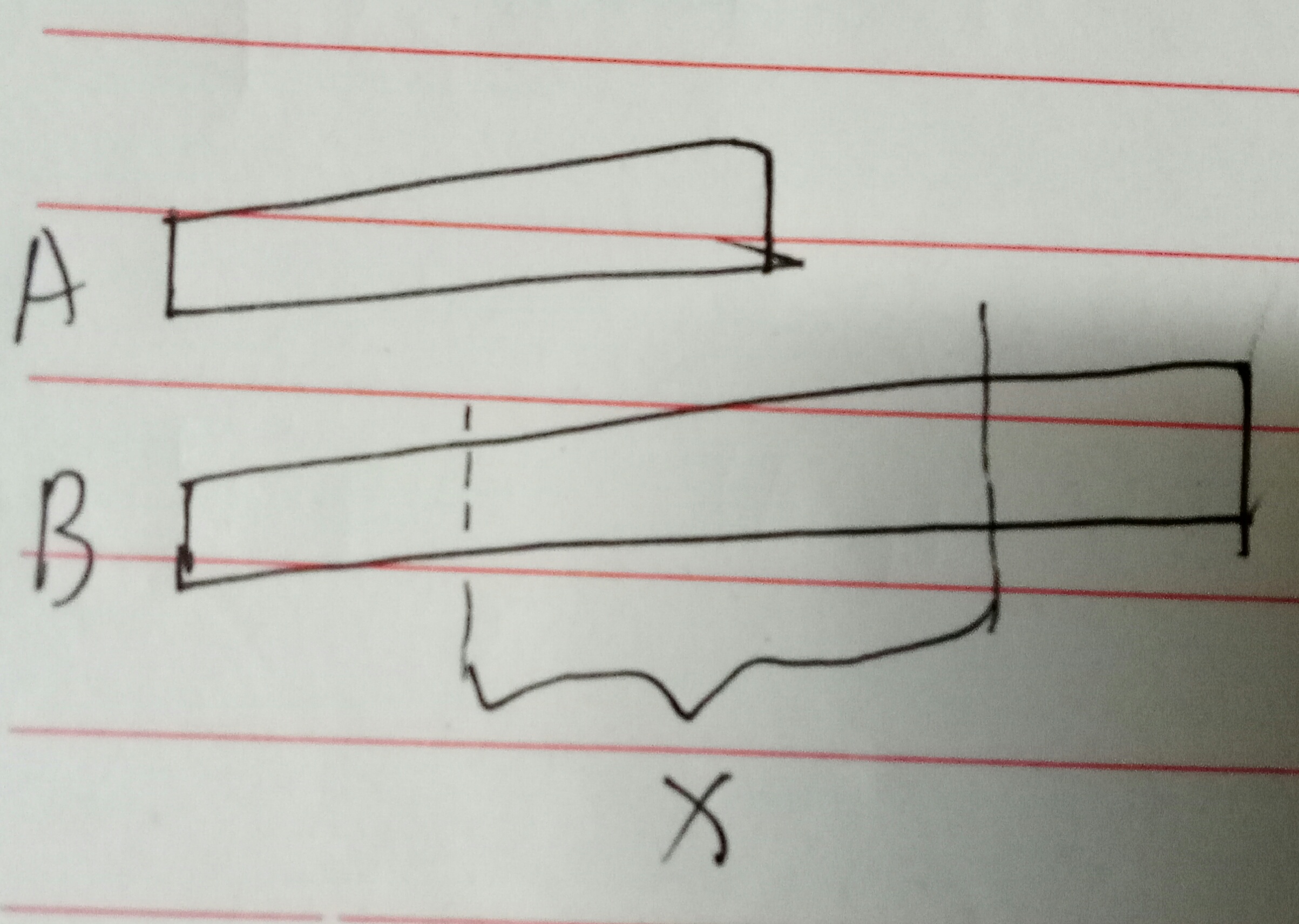
图二：B的x段去匹配A。

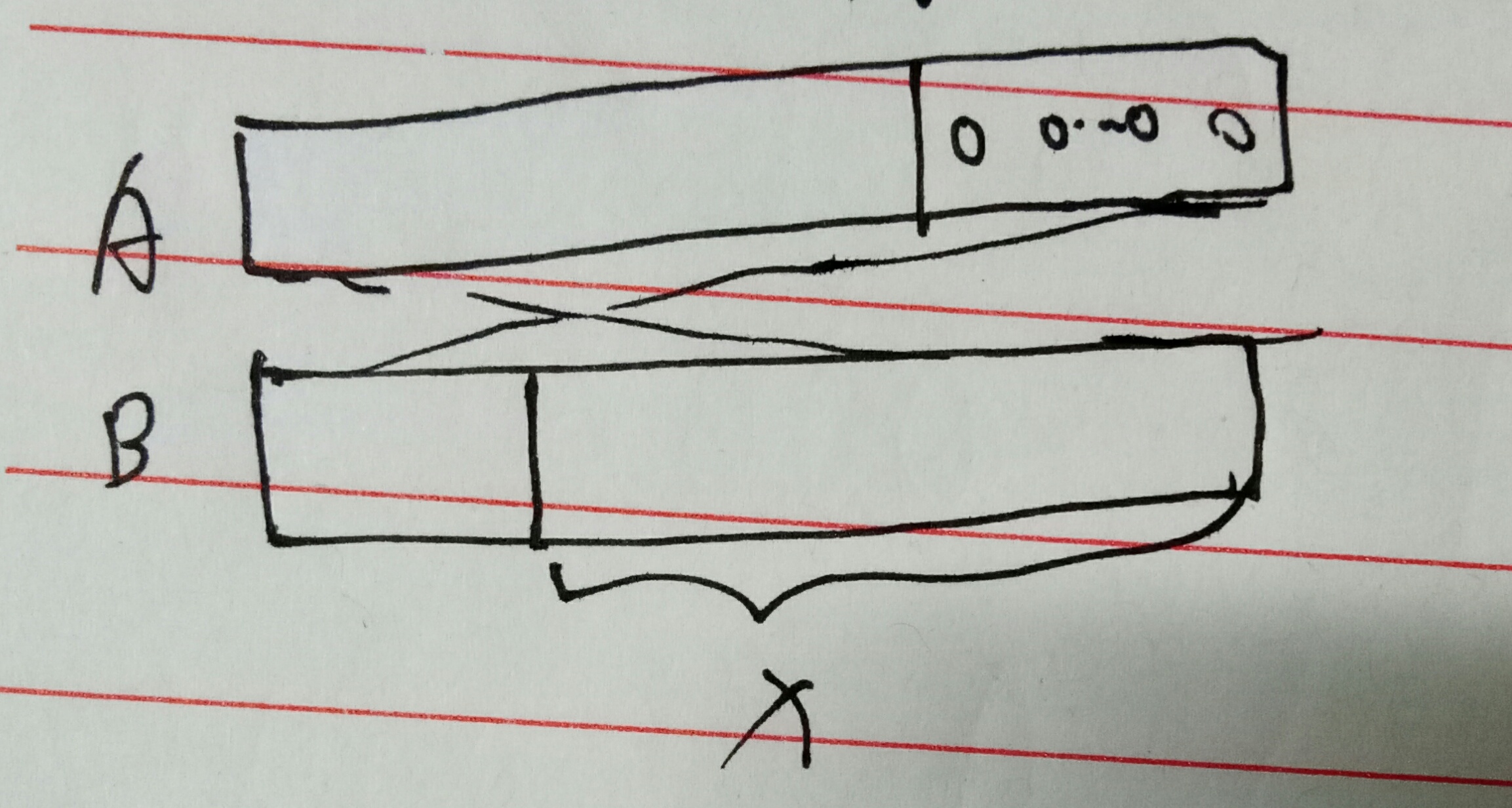
图三：FFT的手段是把原A反转后后面补“0”，变成A'然后求卷积：

B的第一位乘A'的最后一位；B的第二位乘A'的倒二位；B的第三位乘A'的倒三位...B的最后一位匹配A'的第一位

所以会看到B中x前面的部分（b0、b1...bx-1）其实乘的是A后面是“0”，对结果没有影响。

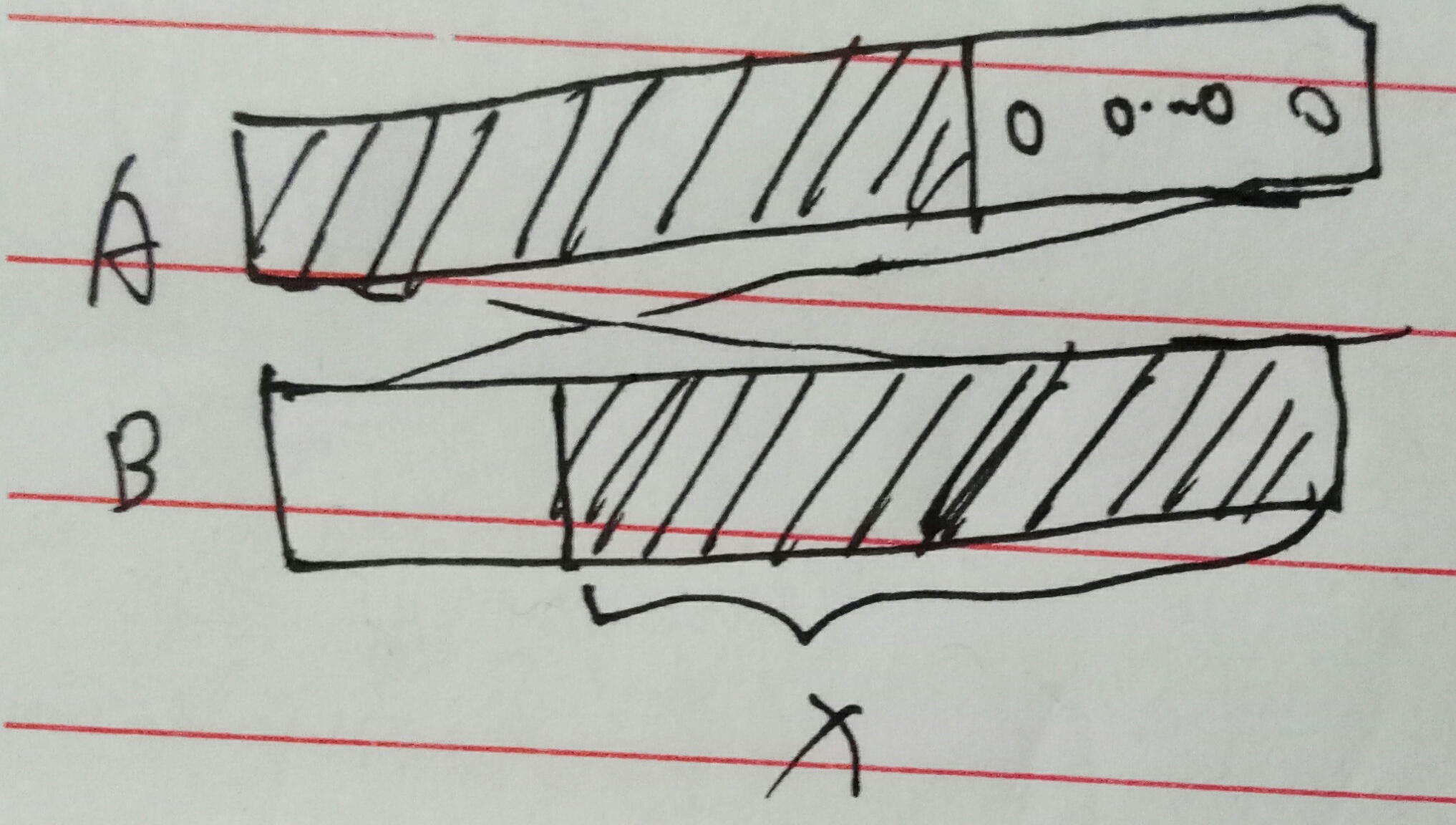
图四：显示的是真正参与匹配的位置，正好就是B的x部分和原来的A的全部。证明方法成立。

所以，我们用F(i)表示B中i为尾的匹配，即：F(i)=A’[0]*B[i]+A’[1]*B[i-1]+A’[2]*B[i-2]+...+A’[i]*B[0]，也即两个序列里下标和为i的A’x和Bi-x相乘。

如果i>=len(A)，且F(i)==0，则以i为尾的部分满足与A匹配。

(所以到现在，字符串的匹配除了常规的hash，kmp，后缀系列之外，  还遇到过bitset，FFT等牛逼技巧，当然splay维护什么的blabla，多得很啊。

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
const int maxn=;
const double pi=acos(-1.0);
using namespace std;
struct complex{
    double r,i;
    complex(){};
    complex(double rr,double ii):r(rr),i(ii){}
    complex friend operator +(complex a,complex b){return (complex){a.r+b.r,a.i+b.i};}
    complex friend operator -(complex a,complex b){return (complex){a.r-b.r,a.i-b.i};}
    complex friend operator *(complex a,complex b){return (complex){a.r*b.r-a.i*b.i,a.r*b.i+a.i*b.r};}
}tmp[maxn];
struct DFT{
    complex a[maxn];
    void fft(int sz,int bg,int step,int opt){
       if(sz==) return;  int m=sz>>;
       fft(m,bg,step<<,opt); fft(m,bg+step,step<<,opt);
       complex w=complex(,),t=complex(cos(2.0*pi/sz),sin(2.0*pi*opt/sz));
       for(int k=;k<m;k++)
       {
            int pos=*step*k;
          tmp[k]=a[pos+bg]+w*a[pos+bg+step];
          tmp[k+m]=a[pos+bg]-w*a[pos+bg+step];
          w=w*t;
       }
       for(int i=;i!=sz;i++) a[i*step+bg]=tmp[i];
    }
}A,B,C;
char c1[maxn],c2[maxn];
int a[maxn],b[maxn],ans[maxn];
int main(){
    int n,m,len=; scanf("%d%d%s%s",&m,&n,c1,c2);
    for(int i=;i<m;i++) if(c1[i]!='*') a[m--i]=c1[i]-'a'+;
    for(int i=;i<n;i++) if(c2[i]!='*') b[i]=c2[i]-'a'+;
    while(len<m+n+) len<<=;

    for(int i=;i<len;i++) A.a[i]=complex(a[i]*a[i]*a[i],), B.a[i]=complex(b[i],);
    A.fft(len,,,); B.fft(len,,,);
    for(int i=;i<len;i++) C.a[i]=C.a[i]+(A.a[i]*B.a[i]);

    for(int i=;i<len;i++) A.a[i]=complex(a[i],), B.a[i]=complex(b[i]*b[i]*b[i],);
    A.fft(len,,,); B.fft(len,,,);
    for(int i=;i<len;i++) C.a[i]=C.a[i]+(A.a[i]*B.a[i]);

    for(int i=;i<len;i++) A.a[i]=complex(a[i]*a[i],), B.a[i]=complex(b[i]*b[i],);
    A.fft(len,,,); B.fft(len,,,);
    for(int i=;i<len;i++) C.a[i]=C.a[i]-complex(,)*(A.a[i]*B.a[i]);

    C.fft(len,,,-);

    for(int i=m-;i<=n;i++) if(C.a[i].r<0.5)  ans[++ans[]]=i-m+;

    printf("%d\n",ans[]);
    for(int i=;i<ans[];i++) printf("%d ",ans[i]);
    printf("%d\n",ans[ans[]]);
    return ;
}