A星算法（Java实现）

一、适用场景

在一张地图中。绘制从起点移动到终点的最优路径，地图中会有障碍物。必须绕开障碍物。

二、算法思路

1. 回溯法得到路径

(假设有路径)採用“结点与结点的父节点”的关系从终于结点回溯到起点，得到路径。

2. 路径代价的估算：F = G+H

A星算法的代价计算使用了被称作是启示式的代价函数。

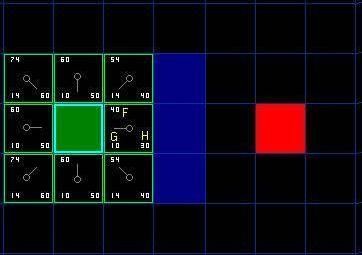
先说明一下各符号意义：G表示的是从起点到当前结点的实际路径代价(为啥叫实际？就是已经走过了，边走边将代价计算好了)。H表示当前结点到达终于结点的预计代价(为啥叫预计？就是还没走过，不知道前面有没障碍、路通不通。所以仅仅能用预计)；F表示当前结点所在路径从起点到终于点预估的总路径代价。

G的计算方式：计算方式有挺多种的，这里我们就用这样的吧，假设每一个结点代表一个正方形，横竖移动距离：斜移动距离=1：1.4（根号2），我们取个整数10和14吧，也就是说当前结点G值=父节点的G+（10或14）。

H的计算方式：估价计算也有非常多种方式，我们这里使用“曼哈顿”法，H=|当前结点x值-终于结点x值|+|当前结点y值-终于结点y值|（”||”表示绝对值）。

例如以下图（图不是自己做的。从网上借来的，自己画的话~…慘不忍睹！）

3. 辅助表：Open、Close列表

在A星算法中，须要使用两个辅助表来记录结点。

一个用于记录可被訪问的结点，成为Open表。一个是记录已訪问过的结点，称为Close表。

这两个表决定了算法的结束：条件是终于结点在Close表中(找到路径)或Open表为空(找不到了路径)。

4. 移动结点、相邻结点的处理

上面的理解的话。如今就来移动当前的节点。寻找路径。

每次从Open表中取出F值最小的结点出来（这里我们使用优先队列来处理比較好），作为当前结点；然后将当前结点的全部邻结点依照邻结点规则增加到Open表中；最后将当前结点放入Close表中。这里就是每次循环的运行内容。

邻结点规则：

(1) 当邻结点不在地图中，不增加Open表；

(2) 当邻结点是障碍物，不增加Open表。

(3) 当邻结点在Close表中。不增加Open表。

(4) 当邻结点不在Open中，增加Open表，设该邻结点的父节点为当前结点；

(5) 当邻结点在Open表中，我们须要做个比較:假设邻结点的G值>当前结点的G值+当前结点到这个邻结点的代价，那么改动该邻结点的父节点为当前的结点(由于在Open表中的结点除了起点。都会有父节点)，改动G值=当前结点的G值+当前结点到这个邻结点的代价

蓝色框框表示在Close表中，绿色的框框表示在Open表中



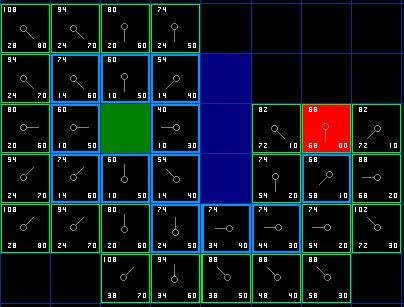
最后回溯得到路径

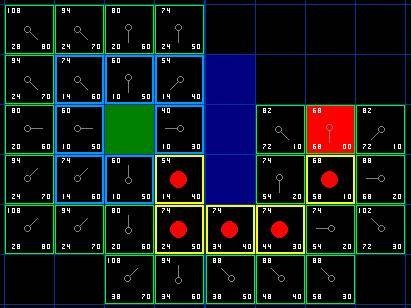
三、代码实现(Java)

1. 输入

(1) 代表地图二值二维数组(0表示可通路。1表示路障)

int[][] maps = {
                { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
                { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
                { 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0 },
                { 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
                { 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0 },
                { 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 },
                { 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 }
                };

(2) 依照二维数组的特点，坐标原点在左上角。所以y是高，x是宽，y向下递增，x向右递增，我们将x和y封装成一个类，好传參，重写equals方法比較坐标(x,y)是不是同一个。

public class Coord
{
    public int x;
    public int y;

    public Coord(int x, int y)
    {
        this.x = x;
        this.y = y;
    }

    @Override
    public boolean equals(Object obj)
    {
        if (obj == null) return false;
        if (obj instanceof Coord)
        {
            Coord c = (Coord) obj;
            return x == c.x && y == c.y;
        }
        return false;
    }
}

(3) 封装路径结点类，字段包含：坐标、G值、F值、父结点。实现Comparable接口，方便优先队列排序。

public class Node implements Comparable<Node>
{

    public Coord coord; // 坐标
    public Node parent; // 父结点
    public int G; // G：是个准确的值。是起点到当前结点的代价
    public int H; // H：是个估值。当前结点到目的结点的预计代价

    public Node(int x, int y)
    {
        this.coord = new Coord(x, y);
    }

    public Node(Coord coord, Node parent, int g, int h)
    {
        this.coord = coord;
        this.parent = parent;
        G = g;
        H = h;
    }

    @Override
    public int compareTo(Node o)
    {
        if (o == null) return -1;
        if (G + H > o.G + o.H)
            return 1;
        else if (G + H < o.G + o.H) return -1;
        return 0;
    }
}

(4) 最后一个数据结构是A星算法输入的全部数据，封装在一起。传參方便。

:grin:

public class MapInfo
{
    public int[][] maps; // 二维数组的地图
    public int width; // 地图的宽
    public int hight; // 地图的高
    public Node start; // 起始结点
    public Node end; // 终于结点

    public MapInfo(int[][] maps, int width, int hight, Node start, Node end)
    {
        this.maps = maps;
        this.width = width;
        this.hight = hight;
        this.start = start;
        this.end = end;
    }
}

2. 处理

(1) 在算法里须要定义几个常量来确定：二维数组中哪个值表示障碍物、二维数组中绘制路径的代表值、计算G值须要的横纵移动代价和斜移动代价。

    public final static int BAR = 1; // 障碍值
    public final static int PATH = 2; // 路径
    public final static int DIRECT_VALUE = 10; // 横竖移动代价
    public final static int OBLIQUE_VALUE = 14; // 斜移动代价

(2) 定义两个辅助表：Open表和Close表。Open表的使用是须要取最小值，在这里我们使用Java工具包中的优先队列PriorityQueue。Close仅仅是用来保存结点，没其它特殊用途。就用ArrayList。

    Queue<Node> openList = new PriorityQueue<Node>(); // 优先队列(升序)
    List<Node> closeList = new ArrayList<Node>();

(3) 定义几个布尔推断方法：终于结点的推断、结点是否能增加open表的推断、结点是否在Close表中的推断。

    /**
     * 推断结点是否是终于结点
     */
    private boolean isEndNode(Coord end,Coord coord)
    {
        return coord != null && end.equals(coord);
    }

    /**
     * 推断结点是否能放入Open列表
     */
    private boolean canAddNodeToOpen(MapInfo mapInfo,int x, int y)
    {
        // 是否在地图中
        if (x < 0 || x >= mapInfo.width || y < 0 || y >= mapInfo.hight) return false;
        // 推断是否是不可通过的结点
        if (mapInfo.maps[y][x] == BAR) return false;
        // 推断结点是否存在close表
        if (isCoordInClose(x, y)) return false;

        return true;
    }

    /**
     * 推断坐标是否在close表中
     */
    private boolean isCoordInClose(Coord coord)
    {
        return coord!=null&&isCoordInClose(coord.x, coord.y);
    }

    /**
     * 推断坐标是否在close表中
     */
    private boolean isCoordInClose(int x, int y)
    {
        if (closeList.isEmpty()) return false;
        for (Node node : closeList)
        {
            if (node.coord.x == x && node.coord.y == y)
            {
                return true;
            }
        }
        return false;
    }

(4) 计算H值，“曼哈顿” 法。坐标分别取差值相加

private int calcH(Coord end,Coord coord)
{
    return Math.abs(end.x - coord.x) + Math.abs(end.y - coord.y);
}

(5) 从Open列表中查找结点

private Node findNodeInOpen(Coord coord)
{
    if (coord == null || openList.isEmpty()) return null;
    for (Node node : openList)
    {
        if (node.coord.equals(coord))
        {
            return node;
        }
    }
    return null;
}

(6) 增加邻结点到Open表

/**
 * 增加全部邻结点到open表
 */
private void addNeighborNodeInOpen(MapInfo mapInfo,Node current)
{
    int x = current.coord.x;
    int y = current.coord.y;
    // 左
    addNeighborNodeInOpen(mapInfo,current, x - 1, y, DIRECT_VALUE);
    // 上
    addNeighborNodeInOpen(mapInfo,current, x, y - 1, DIRECT_VALUE);
    // 右
    addNeighborNodeInOpen(mapInfo,current, x + 1, y, DIRECT_VALUE);
    // 下
    addNeighborNodeInOpen(mapInfo,current, x, y + 1, DIRECT_VALUE);
    // 左上
    addNeighborNodeInOpen(mapInfo,current, x - 1, y - 1, OBLIQUE_VALUE);
    // 右上
    addNeighborNodeInOpen(mapInfo,current, x + 1, y - 1, OBLIQUE_VALUE);
    // 右下
    addNeighborNodeInOpen(mapInfo,current, x + 1, y + 1, OBLIQUE_VALUE);
    // 左下
    addNeighborNodeInOpen(mapInfo,current, x - 1, y + 1, OBLIQUE_VALUE);
}

/**
 * 增加一个邻结点到open表
 */
private void addNeighborNodeInOpen(MapInfo mapInfo,Node current, int x, int y, int value)
{
    if (canAddNodeToOpen(mapInfo,x, y))
    {
        Node end=mapInfo.end;
        Coord coord = new Coord(x, y);
        int G = current.G + value; // 计算邻结点的G值
        Node child = findNodeInOpen(coord);
        if (child == null)
        {
            int H=calcH(end.coord,coord); // 计算H值
            if(isEndNode(end.coord,coord))
            {
                child=end;
                child.parent=current;
                child.G=G;
                child.H=H;
            }
            else
            {
                child = new Node(coord, current, G, H);
            }
            openList.add(child);
        }
        else if (child.G > G)
        {
            child.G = G;
            child.parent = current;
            // 又一次调整堆
            openList.add(child);
        }
    }
}

(7) 回溯法绘制路径

private void drawPath(int[][] maps, Node end)
{
    if(end==null||maps==null) return;
    System.out.println("总代价：" + end.G);
    while (end != null)
    {
        Coord c = end.coord;
        maps[c.y][c.x] = PATH;
        end = end.parent;
    }
}

(8) 開始算法，循环移动结点寻找路径，设定循环结束条件。Open表为空或者终于结点在Close表

public void start(MapInfo mapInfo)
{
    if(mapInfo==null) return;
    // clean
    openList.clear();
    closeList.clear();
    // 開始搜索
    openList.add(mapInfo.start);
    moveNodes(mapInfo);
}

/**
 * 移动当前结点
 */
private void moveNodes(MapInfo mapInfo)
{
    while (!openList.isEmpty())
    {
        if (isCoordInClose(mapInfo.end.coord))
        {
            drawPath(mapInfo.maps, mapInfo.end);
            break;
        }
        Node current = openList.poll();
        closeList.add(current);
        addNeighborNodeInOpen(mapInfo,current);
    }
}

附：源代码地址：点击这里