【CV知识学习】Fisher Vector
在论文《action recognition with improved trajectories》中看到fisher vector,所以学习一下。但网上很多的资料我觉得都写的不好,查了一遍,按照自己的认识陈述一下,望大牛指正。
核函数:
先来看一下《统计学习方法》里叙述的核函数的概念,


可以看到,核函数其实是一个内积,在SVM的公式可以提炼出内积的部分。数据在低维输入空间可能线性不可分,而在高维希尔伯特空间可能线性可分的,因此会经过一个映射函数。事实上,内积中可以理解为相似性即距离。
Fisher核:
Fisher核与Fisher信息矩阵有关,Fisher信息矩阵的意义,在知乎上的答案有了解http://www.zhihu.com/question/26561604。





最后,Fisher核与Fisher信息矩阵有关,得到: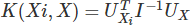 ,而I就是信息矩阵,U就是Score Function。
,而I就是信息矩阵,U就是Score Function。
Fisher Vector在图像上的应用:
图像在这里使用GMM去描述,而图像采集的描述子是在全局范围内的,因此,Fisher向量最后描述的也是全局的特征。一般步骤如下:

先随机选择数据集,去估计GMM的各个参数。Fisher向量应该是Score函数的聚集,但由于会应用到核函数,所以会乘上Fisher信息矩阵。
GMM模型为: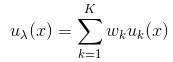
其中(熟悉GMM的人都很容易明白吧),

根据贝叶斯公式,定义描述子属于第i个高斯模型的概率为:
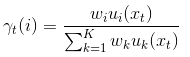
各个参数的Score函数
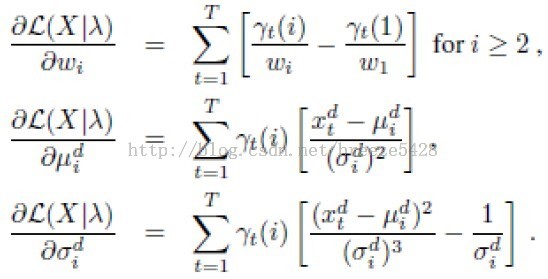
Fisher信息矩阵的近似解为:
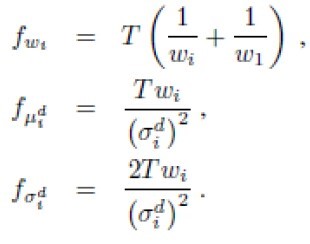
计算FV向量为:
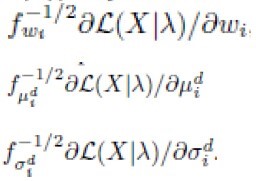
最终的结果为:
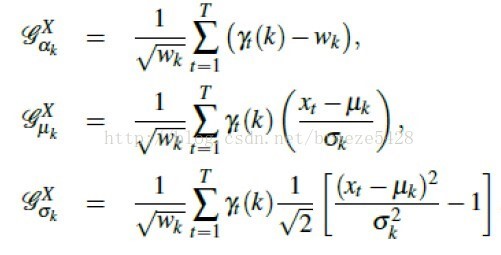
需要注意的是,参数已经在第一步估计出来了。可以看到FV向量的好处是,它把各个大小不同描述子集转化成大小一致的一个特征向量表述。
从原始特征到FV向量的算法表述如下:

其实也没有自己想的东西,本来以为昨晚理解的挺好,今天早上再来想了想,不对啊……直接把知道的写上吧,额,好多博客都没写到点上,哎~~~~~会用就好了~~~~~~~~~~~ T_T
============== 04/12/2016 更==========================
忽然有点明白了,之前一直在想为什么Fisher Vecotr可以作为特征,首先看了两个blog:知乎专栏,CSND
最关键的地方是,fisher vector之所以可以用来做特征分类,还是因为利用了fisher核,注意到它的形式为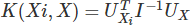 ,而I就是信息矩阵,U就是Score Function。
,而I就是信息矩阵,U就是Score Function。
而fisher 向量的归一化后的每一项,都是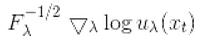 ,即信息矩阵的-1/2次方 * score fucntion。如果两个fisher vector做内积,正好可以得到fisher 核
,即信息矩阵的-1/2次方 * score fucntion。如果两个fisher vector做内积,正好可以得到fisher 核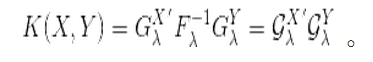
其中信息矩阵为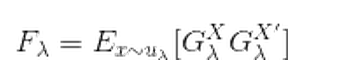
score function 为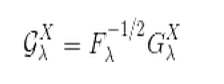
【CV知识学习】Fisher Vector的更多相关文章
- 【CV知识学习】神经网络梯度与归一化问题总结+highway network、ResNet的思考
这是一篇水货写的笔记,希望路过的大牛可以指出其中的错误,带蒟蒻飞啊~ 一. 梯度消失/梯度爆炸的问题 首先来说说梯度消失问题产生的原因吧,虽然是已经被各大牛说烂的东西.不如先看一个简单的网络结构 ...
- 【CV知识学习】early stop、regularation、fine-tuning and some other trick to be known
深度学习有不少的trick,而且这些trick有时还挺管用的,所以,了解一些trick还是必要的.上篇说的normalization.initialization就是trick的一种,下面再总结一下自 ...
- 【CV知识学习】【转】beyond Bags of features for rec scenen categories。基于词袋模型改进的自然场景识别方法
原博文地址:http://www.cnblogs.com/nobadfish/articles/5244637.html 原论文名叫Byeond bags of features:Spatial Py ...
- Fisher Vector Encoding and Gaussian Mixture Model
一.背景知识 1. Discriminant Learning Algorithms(判别式方法) and Generative Learning Algorithms(生成式方法) 现在常见的模式 ...
- 网络知识学习2---(IP地址、子网掩码)(学习还不深入,待完善)
紧接着:网络知识学习1 1.IP地址 IP包头的结构如图 A.B.C网络类别的IP地址范围(图表) A.B.C不同的分配网络数和主机的方式(A是前8个IP地址代表网络,后24个代表主机:B是16 ...
- HTML5标签汇总及知识学习线路总结
HTML5标签汇总,以及知识学习线路总结.
- 安全测试3_Web后端知识学习
其实中间还应该学习下web服务和数据库的基础,对于web服务大家可以回家玩下tomcat或者wamp等东西,数据库的话大家掌握基本的增删该查就好了,另外最好掌握下数据库的内置函数,如:concat() ...
- GCC基础知识学习
GCC基础知识学习 一.GCC编译选项解析 常用编译选项 命令格式:gcc [选项] [文件名] -E:仅执行编译预处理: -S:将C代码转换为汇编代码: -c:仅执行编译操作,不进行连接操作: -o ...
- 毕业设计预习:VHDL入门知识学习(一) VHDL程序基本结构
VHDL入门知识学习(一) VHDL程序基本结构 简介 VHDL程序基本结构 简介 概念: HDL-Hardware Description Language-硬件描述语言-描述硬件电路的功能.信号连 ...
随机推荐
- 在计算机视觉与人工智能领域,顶级会议比SCI更重要(内容转)
很多领域,SCI是王道,尤其在中国,在教师科研职称评审和学生毕业条件中都对SCI极为重视,而会议则充当了补充者的身份.但是在计算机领域,尤其是人工智能与机器学习领域里,往往研究者们更加青睐于会议 我无 ...
- eclipse中folder、source folder和package的区别
今天做ssm项目时,突然发现了这个问题,特别好奇,sqlSessionFactory.xml文件如何找到: 1.放在src/hello目录下: InputStream inputStream = Re ...
- EasyUI tree 异步树与采用扁平化实现的同步树
所谓好记性不如烂笔头,为了以防忘记,才写下这篇博客,废话不多.. 异步树: tips: 可以采用easyui里的原始数据格式,也可以采用扁平化的数据格式. 使用场景: 当菜单模块数量庞大或者无限极 ...
- Mac使用之常用快捷键
正式工作了,公司配给了mac,很多命令跟windows有很大不同,为了自己更好的使用mac本,特此记录平时常用的快捷键命令. 1.复制.保存等:command+c/s等,与windows不同的是ctr ...
- [ Luogu 3927 ] Factorial
\(\\\) \(Description\) 求 \(N!\) 在 \(K\) 进制表示下末尾 \(0\) 的个数. \(N,K\in [1,10^{12}]\) \(\\\) \(Solution\ ...
- 基于SOC方案的嵌入式开发-远程定时设备
Soc方案实现简单的定时开关灯 http://club.gizwits.com/forum.php?mod=viewthread&tid=7787&highlight=%E5%AE%9 ...
- dive into python:模块的导入和搜索文件路径的配置
1.Python中导入模块:import sys:相当于Java中的导入包.类. 比如,我们导入sys模块,使用:import sys; 2.Python中调用函数的时候,会从默认配置的库文件夹中(s ...
- 前端er怎样操作剪切复制以及禁止复制+破解等
前言 有时候我们经常会碰到这些场景:玩掘金.知乎的时候复制一段文字,总是会在内容后面加上一些版权信息,以及像小说网站等都有禁止选中,禁止复制这种功能,还有点击自动复制账号的功能. 我也经常遇到这些场景 ...
- Pro ASP.NET Core MVC 第6版 第二章(前半章)
目录 第二章 第一个MVC 应用程序 学习一个软件开发框架的最好方法是跳进他的内部并使用它.在本章,你将用ASP.NET Core MVC创建一个简单的数据登录应用.我将它一步一步地展示,以便你能看清 ...
- 由DB2分页想到的,关于JDBC ResultSet 处理大数据量
最近在处理DB2 ,查询中,发现如下问题.如果一个查询 count(*),有几十万行,分页如何实现 select row_number() over (order by fid desc ) as r ...
