codeforces_304C_数学题

C. Lucky Permutation Triple

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Bike is interested in permutations. A permutation of length n is an integer sequence such that each integer from 0 to (n - 1) appears exactly once in it. For example, [0, 2, 1] is a permutation of length 3 while both [0, 2, 2] and [1, 2, 3] is not.

A permutation triple of permutations of length n (a, b, c) is called a Lucky Permutation Triple if and only if . The sign ai denotes the i-th element of permutation a. The modular equality described above denotes that the remainders after dividing ai + bi by n and dividing ci by n are equal.

Now, he has an integer n and wants to find a Lucky Permutation Triple. Could you please help him?

Input

The first line contains a single integer n (1 ≤ n ≤ 105).

Output

If no Lucky Permutation Triple of length n exists print -1.

Otherwise, you need to print three lines. Each line contains n space-seperated integers. The first line must contain permutation a, the second line — permutation b, the third — permutation c.

If there are multiple solutions, print any of them.

Examples

input

5

output

1 4 3 2 0
1 0 2 4 3
2 4 0 1 3

input

2

output

-1

Note

In Sample 1, the permutation triple ([1, 4, 3, 2, 0], [1, 0, 2, 4, 3], [2, 4, 0, 1, 3]) is Lucky Permutation Triple, as following holds:

• ;
• ;
• ;
• ;
• .

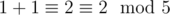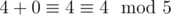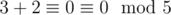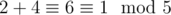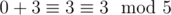In Sample 2, you can easily notice that no lucky permutation triple exists.

题目大意：对于一个整数n有元素是0--n-1的排列，求这样的排列3元组，他满足：
分析：

/* 证明有问题

当n是奇数：

n=1时，0,0,0;
0,1,2，……，n/2，……，n-2，n-1
1,2,3，……，n/2+1，……，n-1，0
1,3,5，……，n，……，2(n-1)-1,n-1 （除最后一个数字都是奇数）
第3行对n取模：1,3,5，……，0，……，n-3，n-1（除了n-1, 趋势：一半奇数，一半偶数）

当n是偶数：
因为偶数不会在取模后改变原数字的奇偶性，所以需要我们构造第三行的数字一半是奇数一半是偶数。
已知：
奇数+奇数=偶数 
偶数+偶数=偶数
奇数+偶数=奇数
所以需要有n/2对奇数+偶数 （1），n/2对同型相加 （2），然而在n是偶数的情况下奇数有n/2个，偶数也是n/2个，在满足（1）的条件下第一行的奇数用完了偶数，所以（2）不能满足。即偶数不能构造3元组。

*/

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int main()
{
    int n,num1[],num2[],num3[];
    scanf("%d",&n);
    if(n%==)
        printf("-1\n");
    else
    {
        for(int i=; i<n; i++)
            num1[i]=i;
        for(int i=; i<n; i++)
            num2[i]=(i+)%n;
        for(int i=; i<n; i++)
            num3[i]=(num1[i]+num2[i])%n;
        for(int i=; i<n; i++)
        {
            printf("%d",num1[i]);
            if(i==n-)
                printf("\n");
            else
                printf(" ");
        }
        for(int i=; i<n; i++)
        {
            printf("%d",num2[i]);
            if(i==n-)
                printf("\n");
            else
                printf(" ");
        }
        for(int i=; i<n; i++)
        {
            printf("%d",num3[i]);
            if(i==n-)
                printf("\n");
            else
                printf(" ");
        }
    }
    return ;
}