P3371 单源最短路径【模板】 洛谷

https://www.luogu.org/problem/show?pid=3371

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

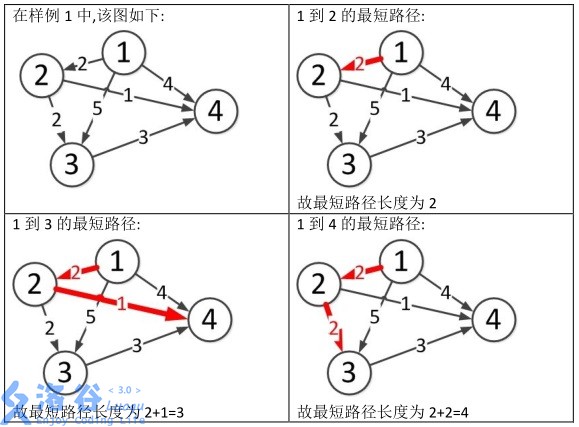
样例说明：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define inf 2147483647
#define maxn 10015
#define ll long long
using namespace std;

ll n,m,s,x,y,z,tot;
ll head[maxn*],d[maxn];
bool vis[maxn];
struct node
{
    ll next,from,val;
}e[];

void add(ll from,ll next,ll val)
{
    tot++;
    e[tot].next=next;
    e[tot].val=val;
    e[tot].from=head[from];
    head[from]=tot;
}

void spfa(ll s)
{
    for(ll i=;i<=n;i++)
        d[i]=inf;
    d[s]=;
    queue<ll>que;
    que.push(s);
    vis[s]=;
    while(!que.empty())
    {
        ll h=que.front();
        que.pop();
        vis[h]=;
        for(ll i=head[h];i!=-;i=e[i].from)
            if(d[e[i].next]>d[h]+e[i].val)
            {
                d[e[i].next]=d[h]+e[i].val;
                if(!vis[e[i].next])
                {
                    que.push(e[i].next);
                    vis[e[i].next]=;
                }
            }
    }
}

int main()
{
    cin>>n>>m>>s;
    memset(head,-,sizeof(head));
    for(ll i=;i<=m;i++)
    {
        cin>>x>>y>>z;
        add(x,y,z);
    }
    spfa(s);
    for(ll i=;i<=n;i++)
        cout<<d[i]<<" ";

    return ;
}