TZOJ 4712 Double Shortest Paths(最小费用最大流)

描述

Alice and Bob are walking in an ancient maze with a lot of caves and one-way passages connecting them. They want to go from cave 1 to cave n. All the passages are difficult to pass. Passages are too small for two people to walk through simultaneously, and crossing a passage can make it even more difficult to pass for the next person. We define di as the difficulty of crossing passage i for the first time, and ai as the additional difficulty for the second time (e.g. the second person's difficulty is di+ai).
Your task is to find two (possibly identical) routes for Alice and Bob, so that their total difficulty is minimized.

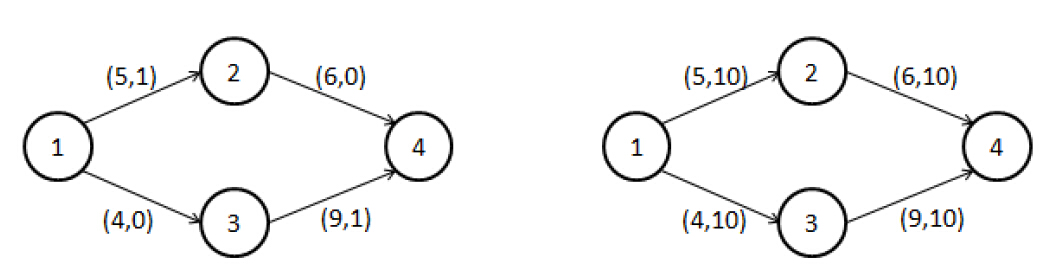
For
example, in figure 1, the best solution is 1->2->4 for both Alice
and Bob, but in figure 2, it's better to use 1->2->4 for Alice
and 1->3->4 for Bob.

输入

There
will be at most 200 test cases. Each case begins with two integers n, m
(1<=n<=500, 1<=m<=2000), the number of caves and passages.
Each of the following m lines contains four integers u, v, di and ai
(1<=u,v<=n, 1<=di<=1000, 0<=ai<=1000). Note that there
can be multiple passages connecting the same pair of caves, and even
passages connecting a cave and itself.

输出

For each test case, print the case number and the minimal total difficulty.

样例输入

4 4
1 2 5 1
2 4 6 0
1 3 4 0
3 4 9 1
4 4
1 2 5 10
2 4 6 10
1 3 4 10
3 4 9 10

样例输出

Case 1: 23
Case 2: 24

题意

找两条从1到N的路使得总花费最小，一条路第一次走花费d，第二次走花费d+a

题解

每个点建两条边一条流量1花费d，一条流量1花费d+a

源点S=0，和1连一条边流量2花费0

汇点T=n+1，和n连一条边流量2花费0

然后跑一边最小费用最大流

代码

 #include<bits/stdc++.h>
 using namespace std;

 const int N=1e5+;
 const int M=2e5+;
 const int INF=0x3f3f3f3f;

 int FIR[N],FROM[M],TO[M],CAP[M],FLOW[M],COST[M],NEXT[M],tote;
 int pre[N],dist[N],q[];
 bool vis[N];
 int n,m,S,T;
 void init()
 {
     tote=;
     memset(FIR,-,sizeof(FIR));
 }
 void addEdge(int u,int v,int cap,int cost)
 {
     FROM[tote]=u;
     TO[tote]=v;
     CAP[tote]=cap;
     FLOW[tote]=;
     COST[tote]=cost;
     NEXT[tote]=FIR[u];
     FIR[u]=tote++;

     FROM[tote]=v;
     TO[tote]=u;
     CAP[tote]=;
     FLOW[tote]=;
     COST[tote]=-cost;
     NEXT[tote]=FIR[v];
     FIR[v]=tote++;
 }
 bool SPFA(int s, int t)
 {
     memset(dist,INF,sizeof(dist));
     memset(vis,false,sizeof(vis));
     memset(pre,-,sizeof(pre));
     dist[s] = ;vis[s]=true;q[]=s;
     int head=,tail=;
     while(head!=tail)
     {
         int u=q[++head];vis[u]=false;
         for(int v=FIR[u];v!=-;v=NEXT[v])
         {
             if(dist[TO[v]]>dist[u]+COST[v]&&CAP[v]>FLOW[v])
             {
                 dist[TO[v]]=dist[u]+COST[v];
                 pre[TO[v]]=v;
                 if(!vis[TO[v]])
                 {
                     vis[TO[v]] = true;
                     q[++tail]=TO[v];
                 }
             }
         }
     }
     return pre[t]!=-;
 }
 void MCMF(int s, int t, int &cost, int &flow)
 {
     flow=;
     cost=;
     while(SPFA(s,t))
     {
         int Min = INF;
         for(int v=pre[t];v!=-;v=pre[TO[v^]])
             Min = min(Min, CAP[v]-FLOW[v]);
         for(int v=pre[t];v!=-;v=pre[TO[v^]])
         {
             FLOW[v]+=Min;
             FLOW[v^]-=Min;
             cost+=COST[v]*Min;
         }
         flow+=Min;
     }
 }
 int main()
 {
     int ca=;
     while(scanf("%d%d",&n,&m)!= EOF)
     {
         init();
         for(int i=,u,v,d,a;i<m;i++)
         {
             scanf("%d%d%d%d",&u,&v,&d,&a);
             addEdge(u,v,,d);
             addEdge(u,v,,d+a);
         }
         S=,T=n+;
         addEdge(S,,,);
         addEdge(n,T,,);
         int cost,flow;
         MCMF(S,T,cost,flow);
         printf("Case %d: %d\n",++ca,cost);
     }
     return ;
 }