Splay模板讲解及一些题目

普通平衡树模板以及文艺平衡树模板链接.

简介

平衡二叉树（Balanced Binary Tree）具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树(摘自百度百科)。

splay又名Splay Balanced Tree(SBT),通过双旋来维持它平衡树的性质.

同时有类似的结构Spaly 我也不知道是不是真的有 , 只用单选来维护平衡树.

struct node{
    int fa;//记录节点父亲
    int ch[2];//ch[0]表示左儿子,ch[1]表示右儿子
    int val;//记录节点权值
    int size;//记录节点子数大小(包括该节点)
    int cnt;//记录同样权值的元素个数
    int mark;//记录反转区间标记(普通平衡树不用)
 }t[N];

另外补充说明一下size在记录子树大小的时候指的是以node为根的整颗子树的元素个数,而不是节点个数(有相同权值的时候都要统计进来).

splay具有这样的性质:

1. 一个节点的权值总比它的左儿子大,比它的右儿子小.
2. splay树的中序遍历结果就是该序列从小到大排列.

下面先介绍一下旋转操作.

旋转首先需要查找一个节点属于左节点还是右节点.

bool get(int x){
    return t[t[x].fa].ch[1] == x;//是右儿子返回1,左儿子返回0
}

并且在将一个节点向上旋的过程中因为节点的关系发生了变化,所以需要重新统计.

void up(int x){
	t[x].size=t[t[x].ch[0]].size+t[t[x].ch[1]].size+t[x].cnt;
}

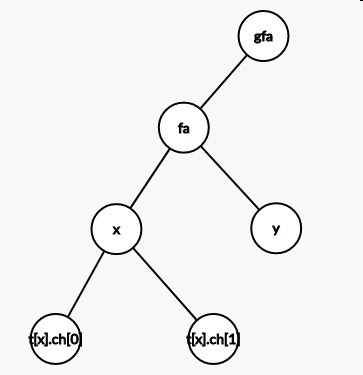
假设现在要将x右旋到fa的位置(向哪个方向旋就叫什么旋),那么步骤如下:

先找出x属于哪边儿子(左儿子还是右儿子):d1(d1为0表示x是左儿子,为1表示是右儿子).图中d1==0(x是左儿子).然后断开x与 t[x].ch[d1^1] 的连边,并将 t[x].ch[d1^1] 连到fa上代替x的位置.

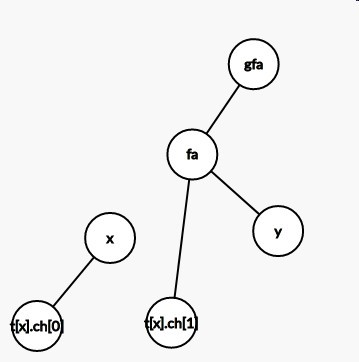
然后断开father与grandfather的连边,将x接上去代替father的位置,并将father以及它整颗子树向下拉.

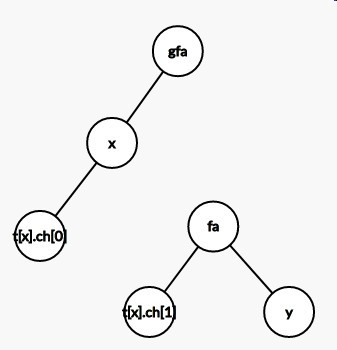
最后再把father与x连边,一次旋转就完成了.

void rotate(int x){
	int fa = t[x].fa , gfa = t[fa].fa;
	int d1 = get(x) , d2 = get(fa);
	t[fa].ch[d1] =  t[x].ch[d1^1] ; t[t[x].ch[d1^1]].fa = fa;
	t[gfa].ch[d2] = x; t[x].fa = gfa;
	t[fa].fa = x; t[x].ch[d1^1] = fa;
	up(fa); up(x);//up是收集节点子树的个数
}

这样旋转后并没有改变它二叉平衡树的性质.并且双旋操作可以减小平衡树的期望深度. (至于为什么可以自己出一组稍微大一点的数据模拟一下)

双旋操作指的是当要旋转的节点与它父亲在同一边时(它和父亲都是左儿子或右儿子),先旋转父亲,再旋转它自己.

play操作其实就是模拟的一个节点向上转的过程,下面直接看注释:

void splay(int x,int goal){//goal是将x旋转到goal的下面
	while(t[x].fa != goal){
	    int fa = t[x].fa , gfa = t[fa].fa;
	    int d1 = get(x) , d2 = get(fa);
	    if(gfa != goal){
		    if(d1 == d2) rotate(fa);//若在同边,则先转father(双旋)
	        else rotate(x);//否则直接将x向上旋
		}
	    rotate(x);//再向上旋一次
	}
    if(goal == 0) root = x;//用goal==0来表示将x转到根节点
}

下面看一下splay过程的图解(splay(x,goal)):

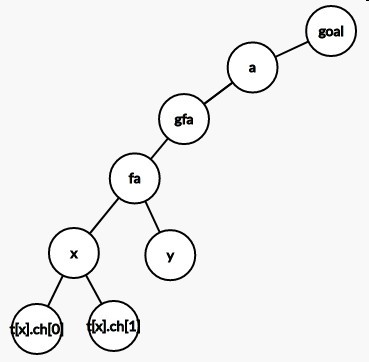
(原图)

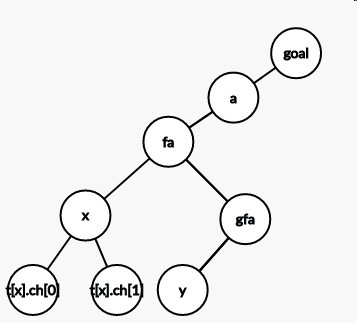
(x与father同侧,先转father)

(再转x)

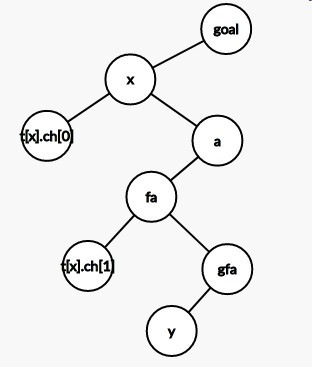
(最后将x旋转到goal的下面).

通过上面这几个函数,我们已经可以维护splay它平衡树的性质了,然后splay还有一些操作:

1. 插入一个数字.
2. 删除一个数字.
3. 查询一个数字的排名.
4. 查找一个数字的前驱/后继.
5. 查询第k小的数字是多少.
6. 查询最值.
   
   
   

首先我们来看如何插入一个数字.

插入节点时是按照新插入的节点权值来遍历splay找到它应该插入的位置的.所以就在遍历splay时记录一下父亲,直到找到应该插入的位置就加新节点.

void insert(int val){
	int node = root , fa = 0;
	while(node && t[node].val != val)
	    fa = node , node = t[node].ch[t[node].val<val];
	if(node) t[node].cnt++;//如果已经存在该权值的节点,则直接给该节点所含相同数字个数++
    else{//否则新开一个编号存节点
	    node = ++cnt; if(fa) t[fa].ch[t[fa].val<val] = node;
	    t[node].fa = fa;
	    t[node].val = val;
	    t[node].cnt = 1;
	    t[node].size = 1;
	}
    splay(node , 0);//将新节点旋到根来维护splay的子树
}

最后将新插入的节点旋到根,新插入节点后的splay树就被维护好了.

查询第k小的数字

我们已经知道了splay的二叉平衡树的性质,并且通过splay操作维持了它平衡树的性质,那么在查询第k小的数字时,就可以直接比较k与节点size的大小来确定第k小的数字在哪个位置了.我们用node来表示当前遍历到的节点(最开始从root出发).

• 如果k比node左子树的size值要小的话,那么第k小一定在node的左子树中.
• 如果k比node左子树和node节点所含数字个数还要多,那么一定在右子树中.
• 如果这两个情况都不满足,则node就是第k小.

int kth(int k){
    int node = root;
    while(1){
		int son = t[node].ch[0];
        if(k <= t[son].size) node = son;
        else if(k > t[son].size+t[node].cnt){
		    k -= t[son].size + t[node].cnt;
		    node = t[node].ch[1];
		}
		else return t[node].val;
	}
}

查询一个数的排名

要查找一个数的排名,首先要找到它在splay树中的位置.同样也是通过权值来遍历.

int find(int val){
	int node = root;
	while(t[node].val!=val && t[node].ch[t[node].val<val])
		node = t[node].ch[t[node].val<val];
	return node;
}

这样找出来的编号就是权值为val的节点.若不存在这样的节点,则会找到叶子节点(此时权值不一定最接近查询的值,但是可以通过这样来找树中的最值).




找到要查的数字后,直接将它旋转到根,此时它左子树的size+1就是它的排名.

int get_rank(int val){
	splay(find(val) , 0);
	return t[t[root].ch[0]].size+1;
}

查找一个数的前驱/后继

为了方便操作,可以先把要查找的值先旋到根.

此时如果要查询前驱,前驱一定就是根节点或是在它的左子树中最大的值.那么先比较根节点的权值与要查询的值,如果要查询前驱并且根节点的权值已经比要找前驱的权值要小了,那么根节点就是要查找的前驱.

为什么一定是这样的呢?因为find找到一个结点要么找到的是该节点,要么就是与要找的权值最接近的节点.所以根节点的权值与查找的权值最接近.而前驱就是比它权值要小的最大的数,所以根节点就是前驱了.

如果根节点不是前驱,那么前驱就是它左子树中的最大值(也就是左子树最右边的节点).

int get_pre(int val,int kind){//前驱后继查询写在了同一个函数里,kind==0表示查找前驱,kind==0表示查找后继
    splay(find(val) , 0); int node = root;
    if(t[node].val<val && kind == 0) return node;
    if(t[node].val>val && kind == 1) return node;//根节点就是前驱/后继的的情况
    node = t[node].ch[kind];
    while(t[node].ch[kind^1])
	    node = t[node].ch[kind^1];//否则找到根节点子树中的最值
	return node;
}

删除一个数

删除一个数,也是先要确定这个节点的位置.但是删除一个节点不能直接将要删除的节点旋转到根.因为如果旋转到根节点之后它有可能还有左右子树.

所以我们可以先找到它的前驱后继,然后将前驱旋到根,后继旋到前驱的下面.此时要删除的点就是后继的左儿子.

因为前驱是第一个比它小的数字,所以它在前驱的右边,后继是第一个比它大的数字,所以他在后继的左边,后继旋到了前驱的下面,那么要删除的节点就一定在前驱后继的中间,也就是后继的左儿子.

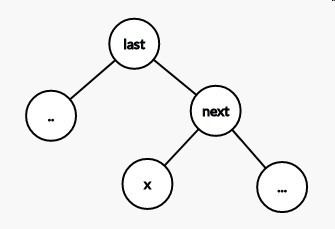
然后找到它的位置进行删除.

void delet(int val){
	int last = get_pre(val,0);
	int next = get_pre(val,1);
	splay(last , 0); splay(next , last);
	if(t[t[next].ch[0]].cnt > 1){
		t[t[next].ch[0]].cnt--;
		splay(t[next].ch[0],0);//同样将未删完的节点转到根重新统计子树大小
	}
	else t[next].ch[0] = 0;//如果能直接删除,则直接去掉这条连边
}

查询最值

查询最值也是通过find函数会找到与一个数最接近的节点的特性,直接find(inf)或者是find(-inf)来找与正无穷最接近的值(最大值)或与负无穷最接近的值(最小值).

到这里,splay的基本操作就讲完了.下面是模板代码.

普通平衡树

#include<bits/stdc++.h>
#define b out(root),cout << endl;
using namespace std;
const int N=100000+5;
const int inf=2147483647;

int n;
int cnt = 0;
int root = 0;

struct splay{
    int ch[2], size, cnt, val, fa;
}t[N];

int gi(){
    int ans = 0 , f = 1; char i = getchar();
    while(i<'0'||i>'9'){if(i=='-')f=-1;i=getchar();}
    while(i>='0'&&i<='9'){ans=ans*10+i-'0';i=getchar();}
    return ans * f;
}

void out(int x){
    if(t[x].ch[0]) out(t[x].ch[0]);
    printf("%d ",t[x].val);
    if(t[x].ch[1]) out(t[x].ch[1]);
}

int get(int x){
    return t[t[x].fa].ch[1] == x;
}

void up(int x){
    t[x].size=t[t[x].ch[0]].size+t[t[x].ch[1]].size+t[x].cnt;
}

void rotate(int x){
    int fa = t[x].fa , gfa = t[fa].fa;
    int d1 = get(x) , d2 = get(fa);
    t[fa].ch[d1]=t[x].ch[d1^1] , t[t[x].ch[d1^1]].fa=fa;
    t[gfa].ch[d2]=x , t[x].fa=gfa;
    t[fa].fa=x , t[x].ch[d1^1]=fa;
    up(fa); up(x);
}

void splay(int x,int goal){
    while(t[x].fa != goal){
	    int fa = t[x].fa, gfa = t[fa].fa;
	    int d1 = get(x), d2 = get(fa);
	    if(gfa != goal){
	        if(d1 == d2) rotate(fa);
	        else rotate(x);
	    }
	    rotate(x);
    }
    if(goal == 0) root = x;
}

int find(int val){
    int node = root;
    while(t[node].val != val && t[node].ch[t[node].val<val])
	    node = t[node].ch[t[node].val<val];
    return node;
}

void insert(int val){
    int node = root, fa = 0;
    while(t[node].val != val && node)
	    fa = node, node = t[node].ch[t[node].val<val];
    if(node) t[node].cnt++;
    else{
	    node = ++cnt;
	    if(fa) t[fa].ch[t[fa].val<val] = node;
	    t[node].size = t[node].cnt = 1;
	    t[node].fa = fa; t[node].val = val;
    }
    splay(node , 0);
}

int pre(int val,int kind){
    splay(find(val) , 0); int node = root;
    if(t[node].val < val && kind == 0) return node;
    if(t[node].val > val && kind == 1) return node;
    node = t[node].ch[kind];
    while(t[node].ch[kind^1])
	    node = t[node].ch[kind^1];
    return node;
}

void delet(int val){
    int last = pre(val,0), next = pre(val,1);
    splay(last , 0); splay(next , last);
    if(t[t[next].ch[0]].cnt > 1){
	    t[t[next].ch[0]].cnt--;
	    splay(t[next].ch[0] , 0);
    }
    else t[next].ch[0] = 0;
}

int kth(int k){
    int node = root;
    if(t[node].size < k) return inf;
    while(1){
	    int son = t[node].ch[0];
	    if(k <= t[son].size) node = son;
	    else if(k > t[son].size+t[node].cnt){
	       k -= t[son].size+t[node].cnt;
	        node = t[node].ch[1];
		}
	    else return t[node].val;
    }
}

int get_rank(int val){
    splay(find(val) , 0);
    return t[t[root].ch[0]].size;
}

int main(){
    insert(-inf); insert(inf);
    int flag, x; n = gi();
    for(int i=1;i<=n;i++){
	    flag = gi(); x = gi();
	    if(flag == 1) insert(x);
	    if(flag == 2) delet(x);
	    if(flag == 3) printf("%d\n",get_rank(x));
	    if(flag == 4) printf("%d\n",kth(x+1));
	    if(flag == 5) printf("%d\n",t[pre(x,0)].val);
	    if(flag == 6) printf("%d\n",t[pre(x,1)].val);
    }
    return 0;
}

当然,这还不够,splay还有一个强大的功能:翻转区间

要找到一段区间,可以利用删除数字的思想.先找到区间左端点的前驱旋转到根,再找到区间右端点的后继旋转到前驱下面,此时要找的区间就能确定就是后继的左子树.然后再给节点打上标记,用线段树的思想不断处理标记,最后再查询的时候再将标记下放,就可以维护出翻转后的序列.

文艺平衡树

#include<bits/stdc++.h>
using namespace std;
const int N=100000+5;
const int inf=2147483647;

int n, m;
int cnt = 0;
int root = 0;

struct node{
    int ch[2], fa, size, mark, val;
}t[N];

bool get(int x){
    return t[t[x].fa].ch[1] == x;
}

void up(int x){
    t[x].size = t[t[x].ch[0]].size + t[t[x].ch[1]].size + 1;
}

void rotate(int x){
	int fa = t[x].fa , gfa = t[fa].fa , d1 = get(x) , d2 = get(fa);
	t[fa].ch[d1] = t[x].ch[d1^1]; t[t[x].ch[d1^1]].fa = fa;
	t[gfa].ch[d2] = x; t[x].fa = gfa;
	t[fa].fa = x; t[x].ch[d1^1] = fa;
	up(fa); up(x);
}

void splay(int x,int goal){
	while(t[x].fa != goal){
	    int fa = t[x].fa , gfa = t[fa].fa;
	    int d1 = get(x) , d2 = get(fa);
	    if(gfa != goal){
	        if(d1 == d2) rotate(fa);
	        else rotate(x);
	    }
	    rotate(x);
	}
	if(goal == 0) root = x;
	//printf("root = %d\n",root);
}

void insert(int val){
	int node = root , fa = 0;
    while(node && t[node].val != val)
	    fa = node , node = t[node].ch[t[node].val<val];
	node = ++cnt;
	if(fa) t[fa].ch[t[fa].val<val] = node;
	t[node].fa = fa;
	t[node].val = val;
	t[node].size = 1;
	splay(node , 0);
}

void pushdown(int x){
	t[t[x].ch[0]].mark ^= 1;
	t[t[x].ch[1]].mark ^= 1;
	t[x].mark = 0;
	swap(t[x].ch[0] , t[x].ch[1]);
}

int kth(int k){
	int node = root;
	while(1){
	    if(t[node].mark) pushdown(node);
	    int son = t[node].ch[0];
	    if(k<=t[son].size) node = son;
	    else if(k>t[son].size+1){
	        k -= t[son].size+1;
	        node = t[node].ch[1];
	    }
	    else return node;
    }
}

void work(int l,int r){
    int left = kth(l) , right = kth(r);
    splay(left , 0) ; splay(right , left);
    t[t[t[root].ch[1]].ch[0]].mark ^= 1;
}

void output(int x){
    if(t[x].mark) pushdown(x);
    if(t[x].ch[0]) output(t[x].ch[0]);
    if(t[x].val>=1 && t[x].val<=n) printf("%d ",t[x].val);
    if(t[x].ch[1]) output(t[x].ch[1]);
}

int main(){
    insert(inf); insert(-inf);
    int x, y; cin >> n >> m;
    for(int i=1;i<=n;i++) insert(i);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
	    work(x , y+2);
    }
    output(root); cout << endl;
    return 0;
}

明白了这几个模板之后,就可以做点简单的题目练练手了.

LIST

1. [HNOI2002]营业额统计
2. [NOI2004]郁闷的出纳员
3. [JSOI2008]最大数
4. [NOI2003]文本编辑器
5. [ZJOI2006]书架
6. [HNOI2004]宠物收养场
7. [HNOI2012]永无乡
8. [NOI2005]维护数列

---

题解

T1:

动态查询前驱并统计答案,没什么好讲的吧.

T2:

对于修改所有人的工资,可以直接用变量保存所有人被修改的工资而不用一个个修改.然后在查询的时候直接找到第一个比劝退标准低的人,删除的时候直接把它以及它左边的全部删掉.也就是在删除的过程中找到它以及它子树的位置旋到根节点的右儿子的左儿子,然后直接删除它的父指针.

T3:

插入的时候直接插入到树的最右边,这样维护的一颗splay的中序遍历结果就是这个序列了.然后在节点维护一个最大值,查找的时候就先找到它前面一个元素的排名旋转到根,那么根节点的右儿子的最大值就是答案了.

T4:

按照题意模拟,可以在插入一个序列的时候先将这个序列处理成一棵树然后再合并.

T5:

可以考虑给每个元素定义一个优先值来维护平衡树的性质(反正当时我做这道题的时候老是搞不清,就这么写了).用一个数组记录一本书的编号映射到树中的优先值.

• 对于要放到书架顶端的书,先将它删除,然后再给它赋一个最小值插入树中.
• 对于要放到书架底端的书同理.
• 对于要与前驱后继交换的书,先交换编号映射的优先值,然后再分别删除,插入这两个点.
• 其他直接模板操作解决.
  
  
  

T6:

因为没有领养者的时候来领养者,或是没有宠物的时候来宠物,都会找到目前树中与该值最接近的一个(前驱后继中取min),所以考虑用一个计数器统计当前领养者/宠物数,来表示目前状态的树为宠物树/领养者树,然后再对这些情况分类讨论一下就可以了.

T7:

链接

<\br>

T8:

按照题意模拟...注意细节,具体代码实现可以戳这里