Codeforces 235E. Number Challenge DP

dp(a,b,c,p) = sigma ( dp(a/p^i,b/p^j,c/p^k) * ( 1+i+j+k) )

表示用小于等于p的素数去分解的结果有多少个

E. Number Challenge

time limit per test

3 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Let's denote d(n) as the number of divisors of a positive integer n.
You are given three integers a, b and c.
Your task is to calculate the following sum:

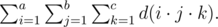
Find the sum modulo 1073741824 (230).

Input

The first line contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 2000).

Output

Print a single integer — the required sum modulo 1073741824 (230).

Sample test(s)

input

2 2 2

output

20

input

4 4 4

output

328

input

10 10 10

output

11536

Note

For the first example.

• d(1·1·1) = d(1) = 1;
• d(1·1·2) = d(2) = 2;
• d(1·2·1) = d(2) = 2;
• d(1·2·2) = d(4) = 3;
• d(2·1·1) = d(2) = 2;
• d(2·1·2) = d(4) = 3;
• d(2·2·1) = d(4) = 3;
• d(2·2·2) = d(8) = 4.

So the result is 1 + 2 + 2 + 3 + 2 + 3 + 3 + 4 = 20.

import java.util.*;

public class CF235E {

	class Triple {

		Triple(){}

		Triple(int _x,int _y,int _z) {
			this.x=_x; this.y=_y; this.z=_z;
			this.sort();
		}

		public int x,y,z;

		void sort() {
			if(this.z<this.y) {
				int t = this.z;
				this.z=this.y;
				this.y=t;
			}
			if(this.z<this.x) {
				int t=this.x;
				this.x=this.z;
				this.z=t;
			}
			if(this.y<this.x) {
				int t=this.x;
				this.x=this.y;
				this.y=t;
			}
		}

		@Override
		public int hashCode() {
			final int prime = 31;
			int result = 1;
			result = prime * result + getOuterType().hashCode();
			result = prime * result + x;
			result = prime * result + y;
			result = prime * result + z;
			return result;
		}

		@Override
		public boolean equals(Object obj) {
			if (this == obj)
				return true;
			if (obj == null)
				return false;
			if (getClass() != obj.getClass())
				return false;
			Triple other = (Triple) obj;
			if (!getOuterType().equals(other.getOuterType()))
				return false;
			if (x != other.x)
				return false;
			if (y != other.y)
				return false;
			if (z != other.z)
				return false;
			return true;
		}

		private CF235E getOuterType() {
			return CF235E.this;
		}
	}

	int a,b,c;
	final int mod = 1073741824 ;

	int[] primes = new int[350];
	int pn=0;

	boolean[] vis = new boolean[2200];

	Map[] map = new Map[333];
	void init() {
		for(int i=2;i<=2100;i++) {
			if(vis[i]==false) {
				primes[pn++]=i;
				for(int j=2*i;j<=2100;j+=i)
					vis[j]=true;
			}
		}
		for(int i=0,j=pn-1;i<=j;i++,j--) {
			int t=primes[i];
			primes[i]=primes[j];
			primes[j]=t;
		}
		for(int i=0;i<333;i++)
			map[i]=new HashMap<Triple,Integer>();
	}

	long gao(int deep,Triple tri) {

		if(deep==pn) return 1;

		if(map[deep].get(tri)!=null) return (long) map[deep].get(tri);
		long ret=0;

		int p=primes[deep];

		for(int x=tri.x,i=0;x!=0;x/=p,i++) {
			for(int y=tri.y,j=0;y!=0;y/=p,j++) {
				for(int z=tri.z,k=0;z!=0;z/=p,k++) {
					ret+=gao(deep+1,new Triple(x,y,z))*(i+j+k+1)%mod;
					if(ret>=mod) {
						ret-=mod;
					}
				}
			}
		}
		map[deep].put(tri, ret);
		return ret;
	}

	CF235E(){
		init();
		Scanner in = new Scanner(System.in);
		a=in.nextInt(); b=in.nextInt(); c=in.nextInt();
		System.out.println(gao(0,new Triple((int)a,(int)b,(int)c)));
	}

	public static void main(String[] args) {
		new CF235E();
	}
}