Floyd判圈算法 Floyd Cycle Detection Algorithm

2018-01-13 20:55:56

Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。该算法据高德纳称由美国科学家罗伯特·弗洛伊德发明，但这一算法并没有出现在罗伯特·弗洛伊德公开发表的著作中。

如果有限状态机、迭代函数或者链表上存在环，那么在某个环上以不同速度前进的2个指针必定会在某个时刻相遇。同时显然地，如果从同一个起点(即使这个起点不在某个环上)同时开始以不同速度前进的2个指针最终相遇，那么可以判定存在一个环，且可以求出2者相遇处所在的环的起点与长度。

一、算法描述

如果有限状态机、迭代函数或者链表存在环，那么一定存在一个起点可以到达某个环的某处(这个起点也可以在某个环上)。

初始状态下，假设已知某个起点节点为节点S。现设两个指针t和h，将它们均指向S。

接着，同时让t和h往前推进，但是二者的速度不同：t每前进1步，h前进2步。只要二者都可以前进而且没有相遇，就如此保持二者的推进。

• 当h无法前进，即到达某个没有后继的节点时，就可以确定从S出发不会遇到环。
• 反之当t与h再次相遇时，就可以确定从S出发一定会进入某个环，设其为环C。

如果确定了存在某个环，就可以求此环的起点与长度。

环长度：上述算法刚判断出存在环C时，显然t和h位于同一节点，设其为节点M。显然，仅需令h不动，而t不断推进，最终又会返回节点M，统计这一次t推进的步数，显然这就是环C的长度。

环入口：为了求出环C的起点，只要令h仍均位于节点M，而令t返回起点节点S，此时h与t之间距为环C长度的整数倍。随后，同时让t和h往前推进，且保持二者的速度相同：t每前进1步，h前进1步。持续该过程直至t与h再一次相遇，设此次相遇时位于同一节点P，则节点P即为从节点S出发所到达的环C的第一个节点，即环C的一个起点。

环入口算法的证明：

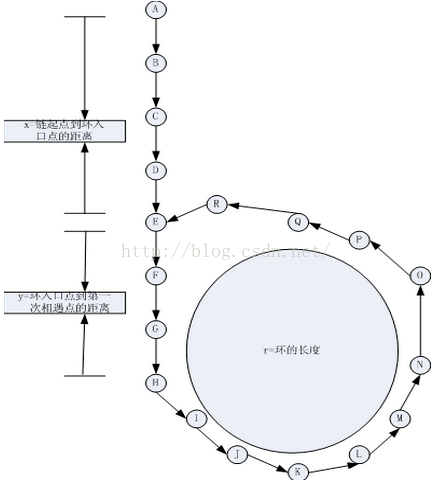
假设慢指针到相遇点的距离为l，则快指针的路程为2l，环的长度为r。

l = x + y；

2l = l + nr；

==> nr = x + y

==> x = nr - y

那么此时，将相遇点的慢指针调到起始点，快指针行进速度和慢指针保持一致，那么当慢指针走了x的路程时，快指针走了nr - y，正好两者在环的入口处相遇。

二、伪代码描述

 1  t := &S
 2  h := &S                                        //令指针t和h均指向起点节点S。
 3  repeat
 4      t := t->next
 5      h := h->next
 6      if h is not NULL                                //要注意这一判断一般不能省略
 7              h := h->next
 8  until t = h or h = NULL
 9  if h != NULL                                       //如果存在环的话
 10     n := 0
 11     repeat                                              //求环的长度
 12             t := t->next
 13             n := n+1
 14     until t = h
 15     t := &S                                     //求环的一个起点
 16     while t != h
 17             t := t->next
 18             h := h->next
 19     P := *t

三、算法复杂度

时间复杂度：注意到当指针t到达环C的一个起点节点P时(此时指针h显然在环C上)，之后指针t最多仅可能走1圈。若设节点S到P距离为m，环C的长度为n，则时间复杂度为O（m+n），是线性时间的算法。

空间复杂度：仅需要创立指针t、指针h，保存环长n、环的一个起点P。空间复杂度为O（1），是常数空间的算法。

四、应用

对于有限状态机与链表，可以判断从某个起点开始是否会返回到访问过运行过程中的某个状态和节点。

对于迭代函数，可以判断其是否存在周期，以及求出其最小正周期。

五、相关算法

虽然Floyd判圈算法已经达到了线性时间复杂度和常数空间复杂度，但是Brent判圈算法将减小时间复杂度的常数系数，平均消耗时间比Floyd判圈算法少36%。

Bruent算法描述：

Bruent算法里有运动的兔子和静止的乌龟。这里的乌龟在兔子行进步数到达step_limit时，会传送到兔子的位置，同时将兔子的行进步数重置为0，同时提高step_limit为原来的两倍。

乌龟和兔子都从名单的顶部开始。兔子每迭代一步。如果是和固定的乌龟一样的位置，那显然是一个循环。如果到达列表的末尾，则没有循环。

为什么要移动乌龟呢？如果一只兔子被卡在一个循环中，没有遇到乌龟，它将永远循环，所以需要将乌龟在一定步数后传送到兔子位置。

为什么每次要花两倍的时间？最终，传送之间的时间长度将比回路的长度更长，因此当兔子完成一圈时，乌龟将在那里等待兔子。

Bruent算法的伪代码描述：

 1 turtle = top
 2 rabbit = top
 3
 4 steps_taken = 0
 5 step_limit = 2
 6
 7 forever:
 8     if rabbit == end:
 9        return 'No Loop Found'
10     rabbit = rabbit.next
11
12     steps_taken += 1
13
14     if rabbit == turtle:
15         return 'Loop found'
16
17     if steps_taken == step_limit:
18         steps_taken = 0
19         step_limit *= 2
20         // teleport the turtle
21         turtle = rabbit

六、相关题目摘录

• Linked List Cycle

问题描述：

问题求解：

    public boolean hasCycle(ListNode head) {
        if (head == null) return false;
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) return true;
        }
        return false;
    }

• Linked List Cycle II

问题描述：

问题求解：

    public ListNode detectCycle(ListNode head) {
        if (head == null) return null;
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) break;
        }
        if (fast == null || fast.next == null) return null;
        slow = head;
        while (slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }

• Happy Number

问题描述：

问题求解：

迭代会生成环，非happy number的环中显然是不可能存在1的，所以如果落入了环中，那么就不可能算得1，否则两者在运算到1后相等。

    public boolean isHappy(int n) {
        int slow = n;
        int fast = n;
        do {
            slow = calc(slow);
            fast = calc(fast);
            fast = calc(fast);
        }while(slow != fast);
        if(slow != 1) return false;
        else return true;
    }

    int calc(int n) {
        int sum = 0;
        while (n > 0) {
            int k = n % 10;
            sum += k*k;
            n /= 10;
        }
        return sum;
    }

• Find the Duplicate Number

问题描述：

问题求解：

经典的判圈算法的题目。

    public int findDuplicate(int[] nums) {
        int slow = 0;
        int fast = 0;
        do {
            slow = nums[slow];
            fast = nums[fast];
            fast = nums[fast];
        } while (slow != fast);
        slow = 0;
        do {
            slow = nums[slow];
            fast = nums[fast];
        } while (slow != fast);
        return slow;
    }