Deep Learning基础--SVD奇异值分解
矩阵奇异值的物理意义是什么?如何更好地理解奇异值分解?下面我们用图片的例子来扼要分析。
矩阵的奇异值是一个数学意义上的概念,一般是由奇异值分解(Singular Value Decomposition,简称SVD分解)得到。如果要问奇异值表示什么物理意义,那么就必须考虑在不同的实际工程应用中奇异值所对应的含义。下面先尽量避开严格的数学符号推导,直观的从一张图片出发,让我们来看看奇异值代表什么意义。
这是女神上野树里(Ueno Juri)的一张照片,像素为高度450*宽度333。
<img src="https://pic2.zhimg.com/50/7aba604694157b53ab901ee4908312cd_hd.jpg" data-rawwidth="498" data-rawheight="536" class="origin_image zh-lightbox-thumb" width="498" data-original="https://pic2.zhimg.com/7aba604694157b53ab901ee4908312cd_r.jpg">我们都知道,图片实际上对应着一个矩阵,矩阵的大小就是像素大小,比如这张图对应的矩阵阶数就是450*333,矩阵上每个元素的数值对应着像素值。我们记这个像素矩阵为
我们都知道,图片实际上对应着一个矩阵,矩阵的大小就是像素大小,比如这张图对应的矩阵阶数就是450*333,矩阵上每个元素的数值对应着像素值。我们记这个像素矩阵为
现在我们对矩阵进行奇异值分解。直观上,奇异值分解将矩阵分解成若干个秩一矩阵之和,用公式表示就是:
其中等式右边每一项前的系数就是奇异值,
和
分别表示列向量,秩一矩阵的意思是矩阵秩为1。注意到每一项
都是秩为1的矩阵。我们假定奇异值满足
(奇异值大于0是个重要的性质,但这里先别在意),如果不满足的话重新排列顺序即可,这无非是编号顺序的问题。
既然奇异值有从大到小排列的顺序,我们自然要问,如果只保留大的奇异值,舍去较小的奇异值,这样(1)式里的等式自然不再成立,那会得到怎样的矩阵——也就是图像?
令,这只保留(1)中等式右边第一项,然后作图:
<img src="https://pic2.zhimg.com/50/ba727031b6fe9449ad3d67caeecf9795_hd.jpg" data-rawwidth="498" data-rawheight="536" class="origin_image zh-lightbox-thumb" width="498" data-original="https://pic2.zhimg.com/ba727031b6fe9449ad3d67caeecf9795_r.jpg">结果就是完全看不清是啥……我们试着多增加几项进来: 结果就是完全看不清是啥……我们试着多增加几项进来:
结果就是完全看不清是啥……我们试着多增加几项进来:,再作图
<img src="https://pic1.zhimg.com/50/26af24cb31adec4d4e16939798fe4f18_hd.jpg" data-rawwidth="498" data-rawheight="536" class="origin_image zh-lightbox-thumb" width="498" data-original="https://pic1.zhimg.com/26af24cb31adec4d4e16939798fe4f18_r.jpg">隐约可以辨别这是短发伽椰子的脸……但还是很模糊,毕竟我们只取了5个奇异值而已。下面我们取20个奇异值试试,也就是(1)式等式右边取前20项构成 隐约可以辨别这是短发伽椰子的脸……但还是很模糊,毕竟我们只取了5个奇异值而已。下面我们取20个奇异值试试,也就是(1)式等式右边取前20项构成
隐约可以辨别这是短发伽椰子的脸……但还是很模糊,毕竟我们只取了5个奇异值而已。下面我们取20个奇异值试试,也就是(1)式等式右边取前20项构成
<img src="https://pic2.zhimg.com/50/7f70625c040ddfc9ed2681365c37c8e5_hd.jpg" data-rawwidth="498" data-rawheight="536" class="origin_image zh-lightbox-thumb" width="498" data-original="https://pic2.zhimg.com/7f70625c040ddfc9ed2681365c37c8e5_r.jpg">虽然还有些马赛克般的模糊,但我们总算能辨别出这是Juri酱的脸。当我们取到(1)式等式右边前50项时: 虽然还有些马赛克般的模糊,但我们总算能辨别出这是Juri酱的脸。当我们取到(1)式等式右边前50项时:
虽然还有些马赛克般的模糊,但我们总算能辨别出这是Juri酱的脸。当我们取到(1)式等式右边前50项时:
<img src="https://pic2.zhimg.com/50/15eecd833bd9c0c6d5a4d33c044f5945_hd.jpg" data-rawwidth="498" data-rawheight="536" class="origin_image zh-lightbox-thumb" width="498" data-original="https://pic2.zhimg.com/15eecd833bd9c0c6d5a4d33c044f5945_r.jpg">我们得到和原图差别不大的图像。也就是说当
我们得到和原图差别不大的图像。也就是说当从1不断增大时,
不断的逼近
。让我们回到公式
矩阵表示一个450*333的矩阵,需要保存
个元素的值。等式右边
和
分别是450*1和333*1的向量,每一项有
个元素。如果我们要存储很多高清的图片,而又受限于存储空间的限制,在尽可能保证图像可被识别的精度的前提下,我们可以保留奇异值较大的若干项,舍去奇异值较小的项即可。例如在上面的例子中,如果我们只保留奇异值分解的前50项,则需要存储的元素为
,和存储原始矩阵
相比,存储量仅为后者的26%。
下面可以回答题主的问题:奇异值往往对应着矩阵中隐含的重要信息,且重要性和奇异值大小正相关。每个矩阵都可以表示为一系列秩为1的“小矩阵”之和,而奇异值则衡量了这些“小矩阵”对于
的权重。
在图像处理领域,奇异值不仅可以应用在数据压缩上,还可以对图像去噪。如果一副图像包含噪声,我们有理由相信那些较小的奇异值就是由于噪声引起的。当我们强行令这些较小的奇异值为0时,就可以去除图片中的噪声。如下是一张25*15的图像(本例来源于[1])
<img src="https://pic4.zhimg.com/50/39f209faded179e3ba45b9304d137b77_hd.jpg" data-rawwidth="150" data-rawheight="250" class="content_image" width="150">但往往我们只能得到如下带有噪声的图像(和无噪声图像相比,下图的部分白格子中带有灰色): 但往往我们只能得到如下带有噪声的图像(和无噪声图像相比,下图的部分白格子中带有灰色):
但往往我们只能得到如下带有噪声的图像(和无噪声图像相比,下图的部分白格子中带有灰色):
<img src="https://pic1.zhimg.com/50/154413815249e578abad23acaf6dfe98_hd.jpg" data-rawwidth="150" data-rawheight="250" class="content_image" width="150">通过奇异值分解,我们发现矩阵的奇异值从大到小分别为:14.15,4.67,3.00,0.21,……,0.05。除了前3个奇异值较大以外,其余奇异值相比之下都很小。强行令这些小奇异值为0,然后只用前3个奇异值构造新的矩阵,得到 通过奇异值分解,我们发现矩阵的奇异值从大到小分别为:14.15,4.67,3.00,0.21,……,0.05。除了前3个奇异值较大以外,其余奇异值相比之下都很小。强行令这些小奇异值为0,然后只用前3个奇异值构造新的矩阵,得到
通过奇异值分解,我们发现矩阵的奇异值从大到小分别为:14.15,4.67,3.00,0.21,……,0.05。除了前3个奇异值较大以外,其余奇异值相比之下都很小。强行令这些小奇异值为0,然后只用前3个奇异值构造新的矩阵,得到
<img src="https://pic3.zhimg.com/50/1df92ac5dc018d63b14c30ae92eff222_hd.jpg" data-rawwidth="150" data-rawheight="250" class="content_image" width="150">可以明显看出噪声减少了(白格子上灰白相间的图案减少了)。
可以明显看出噪声减少了(白格子上灰白相间的图案减少了)。
奇异值分解还广泛的用于主成分分析(Principle Component Analysis,简称PCA)和推荐系统(如Netflex的电影推荐系统)等。在这些应用领域,奇异值也有相应的意义。
考虑题主在问题描述中的叙述:“把m*n矩阵看作从m维空间到n维空间的一个线性映射,是否:各奇异向量就是坐标轴,奇异值就是对应坐标的系数?”我猜测,题主更想知道的是奇异值在数学上的几何含义,而非应用中的物理意义。下面简单介绍一下奇异值的几何含义,主要参考文献是美国数学协会网站上的文章[1]。
下面的讨论需要一点点线性代数的知识。线性代数中最让人印象深刻的一点是,要将矩阵和空间中的线性变换视为同样的事物。比如对角矩阵作用在任何一个向量上
其几何意义为在水平方向上拉伸3倍,
方向保持不变的线性变换。换言之对角矩阵起到作用是将水平垂直网格作水平拉伸(或者反射后水平拉伸)的线性变换。
<img src="https://pic2.zhimg.com/50/012f667312babcd48d6548740b263645_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252"> <img src="https://pic1.zhimg.com/50/83c8636e531a0df1795db6ca4f4f3758_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">如果
<img src="https://pic1.zhimg.com/50/83c8636e531a0df1795db6ca4f4f3758_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">如果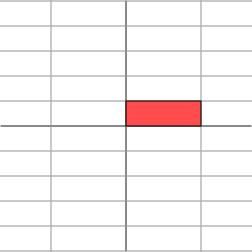 如果
如果不是对角矩阵,而是一个对称矩阵
那么,我们也总可以找到一组网格线,使得矩阵作用在该网格上仅仅表现为(反射)拉伸变换,而没有旋转变换
<img src="https://pic2.zhimg.com/50/8acc7767cfbb297043a13b2e8f2e9329_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252"> <img src="https://pic1.zhimg.com/50/3f9674bd72eaa879f353a0d368033824_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">考虑更一般的
<img src="https://pic1.zhimg.com/50/3f9674bd72eaa879f353a0d368033824_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">考虑更一般的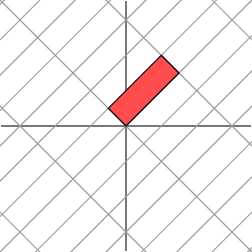 考虑更一般的非对称矩阵
考虑更一般的非对称矩阵
很遗憾,此时我们再也找不到一组网格,使得矩阵作用在该网格上之后只有拉伸变换(找不到背后的数学原因是对一般非对称矩阵无法保证在实数域上可对角化,不明白也不要在意)。我们退求其次,找一组网格,使得矩阵作用在该网格上之后允许有拉伸变换和旋转变换,但要保证变换后的网格依旧互相垂直。这是可以做到的
<img src="https://pic2.zhimg.com/50/356babf4c08d6c0fefc05195ab5da6c1_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252"> <img src="https://pic1.zhimg.com/50/73a69c76a7de9ec012f0ad0240cad6b8_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">下面我们就可以自然过渡到奇异值分解的引入。
<img src="https://pic1.zhimg.com/50/73a69c76a7de9ec012f0ad0240cad6b8_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">下面我们就可以自然过渡到奇异值分解的引入。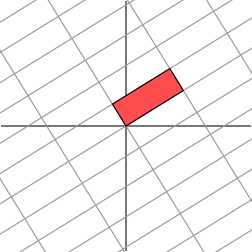 下面我们就可以自然过渡到奇异值分解的引入。奇异值分解的几何含义为:对于任何的一个矩阵,我们要找到一组两两正交单位向量序列,使得矩阵作用在此向量序列上后得到新的向量序列保持两两正交。下面我们要说明的是,奇异值的几何含义为:这组变换后的新的向量序列的长度。
下面我们就可以自然过渡到奇异值分解的引入。奇异值分解的几何含义为:对于任何的一个矩阵,我们要找到一组两两正交单位向量序列,使得矩阵作用在此向量序列上后得到新的向量序列保持两两正交。下面我们要说明的是,奇异值的几何含义为:这组变换后的新的向量序列的长度。
<img src="https://pic4.zhimg.com/50/b62ae777cc9c9234702f61989e59aedf_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252"> <img src="https://pic4.zhimg.com/50/df96a8b5c3b45c90924d4f11b007ca47_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">当矩阵
<img src="https://pic4.zhimg.com/50/df96a8b5c3b45c90924d4f11b007ca47_hd.jpg" data-rawwidth="252" data-rawheight="252" class="content_image" width="252">当矩阵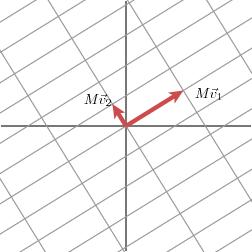
当矩阵作用在正交单位向量
和
上之后,得到
和
也是正交的。令
和
分别是
和
方向上的单位向量,即
,
,写在一起就是
,整理得:
这样就得到矩阵的奇异值分解。奇异值
和
分别是
和
的长度。很容易可以把结论推广到一般
维情形。
下面给出一个更简洁更直观的奇异值的几何意义(参见[2])。先来一段线性代数的推导,不想看也可以略过,直接看黑体字几何意义部分:
假设矩阵的奇异值分解为
其中是二维平面的向量。根据奇异值分解的性质,
线性无关,
线性无关。那么对二维平面上任意的向量
,都可以表示为:
。
当作用在
上时,
令,我们可以得出结论:如果
是在单位圆
上,那么
正好在椭圆
上。这表明:矩阵
将二维平面中单位圆变换成椭圆,而两个奇异值正好是椭圆的两个半轴长,长轴所在的直线是
,短轴所在的直线是
.
推广到一般情形:一般矩阵将单位球
变换为超椭球面
,那么矩阵
的每个奇异值恰好就是超椭球的每条半轴长度。
<img src="https://pic4.zhimg.com/50/34ca30b59f8f462f4aa552f807d2e867_hd.jpg" data-rawwidth="494" data-rawheight="232" class="origin_image zh-lightbox-thumb" width="494" data-original="https://pic4.zhimg.com/34ca30b59f8f462f4aa552f807d2e867_r.jpg">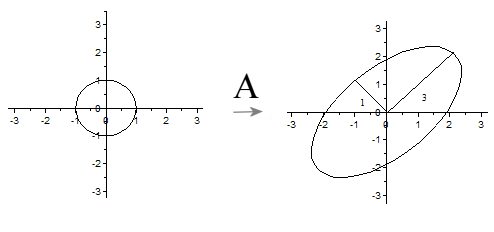
链接:https://www.zhihu.com/question/22237507/answer/53804902
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
参考文献:
[1] We Recommend a Singular Value Decomposition(Feature Column from the AMS)
[2] 徐树方,《矩阵计算的理论与方法》,北京大学出版社。
Deep Learning基础--SVD奇异值分解的更多相关文章
- Deep Learning基础--理解LSTM/RNN中的Attention机制
导读 目前采用编码器-解码器 (Encode-Decode) 结构的模型非常热门,是因为它在许多领域较其他的传统模型方法都取得了更好的结果.这种结构的模型通常将输入序列编码成一个固定长度的向量表示,对 ...
- Deep Learning基础--CNN的反向求导及练习
前言: CNN作为DL中最成功的模型之一,有必要对其更进一步研究它.虽然在前面的博文Stacked CNN简单介绍中有大概介绍过CNN的使用,不过那是有个前提的:CNN中的参数必须已提前学习好.而本文 ...
- Deep Learning基础--参数优化方法
1. 深度学习流程简介 1)一次性设置(One time setup) -激活函数(Activation functions) - 数据预处理(Data Preprocessing) ...
- Deep Learning基础--26种神经网络激活函数可视化
在神经网络中,激活函数决定来自给定输入集的节点的输出,其中非线性激活函数允许网络复制复杂的非线性行为.正如绝大多数神经网络借助某种形式的梯度下降进行优化,激活函数需要是可微分(或者至少是几乎完全可微分 ...
- Deep Learning基础--理解LSTM网络
循环神经网络(RNN) 人们的每次思考并不都是从零开始的.比如说你在阅读这篇文章时,你基于对前面的文字的理解来理解你目前阅读到的文字,而不是每读到一个文字时,都抛弃掉前面的思考,从头开始.你的记忆是有 ...
- Deep Learning基础--Softmax求导过程
一.softmax函数 softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类! 假设我们有一个数组,V,Vi表示V中的第i个元素,那么这个 ...
- Deep Learning基础--随时间反向传播 (BackPropagation Through Time,BPTT)推导
1. 随时间反向传播BPTT(BackPropagation Through Time, BPTT) RNN(循环神经网络)是一种具有长时记忆能力的神经网络模型,被广泛用于序列标注问题.一个典型的RN ...
- Deep Learning基础--各个损失函数的总结与比较
损失函数(loss function)是用来估量你模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好.损失函数是经验 ...
- Deep Learning基础--word2vec 中的数学原理详解
word2vec 是 Google 于 2013 年开源推出的一个用于获取 word vector 的工具包,它简单.高效,因此引起了很多人的关注.由于 word2vec 的作者 Tomas Miko ...
随机推荐
- idea Class<>表示的含义
- 当对象使用sort时候 前提是实现compareTo的方法
- BZOJ4899 记忆的轮廓(概率期望+动态规划+决策单调性)
容易发现跟树没什么关系,可以预处理出每个点若走向分叉点期望走多少步才能回到上个存档点,就变为链上问题了.考虑dp,显然有f[i][j]表示在i~n中设置了j个存档点,其中i设置存档点的最优期望步数.转 ...
- (转)linux下压缩和归档相关命令tar,zip,gzip,bzip2
压缩包也有两种形式,一种是tar.gz包(.tgz包也是这种),一种是tar.bz2包. tar.gz包的解压方法:tar zxvf [PackageName].tar.gz tar.bz2包的解压方 ...
- elasticsearch 第五篇(文档操作接口)
INDEX API 示例: 1 2 3 4 5 PUT /test/user/1 { "name": "silence", "age": 2 ...
- OpenFlow 消息
消息类型 OpenFlow 的消息共分为三类: Controller-to-Switch 顾名思义,此类消息是由控制器主动发出 Features 用于获取交换机特性 Configuration 用于配 ...
- BZOJ 3786: 星系探索 解题报告
3786: 星系探索 Description 物理学家小C的研究正遇到某个瓶颈. 他正在研究的是一个星系,这个星系中有n个星球,其中有一个主星球(方便起见我们默认其为1号星球),其余的所有星球均有且仅 ...
- 洛谷 P3373 【模板】线段树 2 解题报告
P3373 [模板]线段树 2 题目描述 如题,已知一个数列,你需要进行下面三种操作: 1.将某区间每一个数乘上\(x\) 2.将某区间每一个数加上\(x\) 3.求出某区间每一个数的和 输入输出格式 ...
- 20135239益西拉姆 Linux内核分析 操作系统是怎样工作的?
益西拉姆+ 原创作品+ <Linux内核分析>MOOC课程http://mooc.study.163.com/course/USTC-1000029000 ” 堆栈 堆栈是C语言程序运行时 ...
- SpringMVC 之 表单标签
本篇我们来学习Spring MVC表单标签的使用,借助于Spring MVC提供的表单标签可以让我们在视图上展示WebModel中的数据更加轻松. 一.首先我们先做一个简单了例子来对Spring MV ...
