Codeforces - tag::graphs 大合集 [占坑]

520B

给定初始n和目标m,存在两种操作$-1$和$×2$,要求最少操作次数

无脑解法是BFS,不能解决稍大的规模

当n>m时,输出n-m

否则逆向处理,转换为m到n的最小操作次数,存在两种操作$+1$和$/2$(后者只能在偶数时操作)

由$(m+1+1)/2=m/2+1$得尽量多的/2操作可以减少操作次数

因此若操作当前的$m$是偶数时尽量/2,直到$m≤n$时再多操作$(n-m)$次$+1$是最优操作

Challenge: suppose we have a generalized problem: we want to get n starting from m using two operations "subtract a" and "multiply by b". Generalize the solution to find the minimal number of moves to get from n to m in 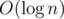time if a and b are coprime. Can you do it if a and b may have common divisors greater than 1?

339C

给出砝码,限定重量类型但个数无限,求能否在天平上按照规则操作$m$次并输出方案

规则1.每次使用的砝码不能与上一次的相同重量

规则2:每次放入砝码后该侧的重量比另一侧天平的重量大

我的想法:设$dp[i][j][k]$:第$i$次放入重量为$j$的砝码使另一侧的天平为$k$

$dp[i][j][k]=dp[i-1][x≠j][y<sum...]$

但官方题解用到了平衡的想法来替代sum

那么$dp[i][j][k]$:存在第$i$次放入重量为$j$的砝码使两侧平衡差为$k$的方案

$dp[i][j][k]=dp[i-1][x≠j][y=j-k>0]$ ,只需存在一对$(x,y)$该方程既为真

说明:记上一次平衡差为$y$,假设砝码放在左边,则$l-r=y$

这次在右边平衡差为$k$,则$r'-l'=k,l'=l,r'=r+j$

$∴y=j-k$

295B

给定一个图,顶点数$n≤500$,图中每对顶点都有两条边分别指向从对中某一点指向另一点,且权值给出

再给定一个删除序列$x[1...n]$,表示要按顺序删除某个点,求每次序列操作前剩余的所有点对的最短距离之和

逆向考虑,floyd三重循环最外层为加入顶点的顺序,那我们把删除序列翻转过来就变为添加序列,既是一个floyd的过程

实现细节上的注意,添加$x[k]$点后先把$x[k]$相关的所有边都优先松弛再进行内循环更新

PS.做完这道题后对floyd的细节有了船新的认识

https://paste.ubuntu.com/p/YVHzf8pk8R/

329B(水)

从起点走到终点，其中有些地方不能走，有些地方存在一些敌人（0~9），且能和我们一样正常移动或者是停留，每次动作都是一个单位的时间，而敌人总是尽量杀向你。求起点到终点能最少干掉敌人的数目。

要注意到的一点是必然能拦截自己的肯定是它们到终点的距离小于自己到终点的距离

然后从终点BFS就ok了

916C(水)

构造一个n个点m条边的图,使得其1到n最短路距离为素数,MST之和为素数,且没环和重边

很显然构造一条链凑数就好

472D(水)

构造一棵树，使得该树中各点对的距离与给出原矩阵的距离相等

不知道为什么，在纸上画了一下就觉得是MST，然后暴力dijkstra检查匹配与否

https://paste.ubuntu.com/p/Cp72FznfkG/

242C(疑)

想了一下没找到快速有效的表示方法，网上题解甚至敢1e9logn暴力
暂时搁置

954D

给了n个点和m条边，还给了起点s和终点t，问最多加多少条边，可以使得起点到终点的最短路不会变小。

分开两边求sssp，然后枚举不存在的边的两个dis的可能性
$dis1[i]+1+dis2[j]≥dis1[ed] \ \& \ dis2[i]+1+dis1[j]≥dis2[st]$

543B

给定一个无向边无权图，给出两个起点$s_i$终点$t_i$和约束条件$l_i$
求最多删除的边数使得$dis[s_1][t_1]≤l_1 \ \& \ dis[s_2][t_2]≤l_2$
首先无相关的边（不在最短路径上的边）肯定是要被叉的
其次最短路径上的边也是可能被叉的，但这时候叉的某一路径可能会影响到两条最短路径
因此暴力枚举共享的端点，计算出当前最短路径下的总边数更新答案（注意枚举是有向的）
也可以想象成不断添加边构成新的符合约束的最短路
https://paste.ubuntu.com/p/PHrBpfXp9y/

25C(水)

给定一个图,每次添加一条边,对所有最短点对距离和

改动floyd,每次只$O(n^2)$更新相关的点

https://paste.ubuntu.com/p/spnMWJSKf3/

229B(水)

普通sssp,存在限制:某时刻某些节点不可经过

每次访问节点时先计算出连续被屏蔽的时间长即可

https://paste.ubuntu.com/p/MS5j4jjbWV/

61D

给定一棵树,求从点1到各点的边权和最小

贪心的做法,找出起点为1的最长的路径,剩下的边都遍历2遍

https://paste.ubuntu.com/p/hdTdHxdgQx/

877D(水)

从起点开始可往四个方向跑,每个方向可走1-k步(障碍物除外),问到达终点的最小时间

预判要走的方向,如果该方向上存在比当前时间还短的状态就无需往后(i-k)搜索

实现上可能有坑,不敲了

14D

给出一棵树，找出两条不相交即没有公共点的路径，使得两个路径的长度的乘积最大。

枚举树中的边，将该边去掉，分成两棵树，分别求出这两棵树的直径，乘起来维护一个最大值即可。

938D

给定一个图,图的自定义终点有点权,求每一个起点到某一个终点的最小点权边权和(其中边要往返,既乘2)

多个源点不定终点看着有点难办,要尝试倒着求,给每个点的连接到汇点$S$,边权为该点的点权,然后剩余的边权全部乘2

那么从S出发的SSSP就是对应的原题过程的逆过程,由此解得

PS.本题存在代码歧视,差不多一样的写法愣是MLE个10倍艹,不提供代码了

SP Last UPD:7.3