机器学习算法（优化）之一：梯度下降算法、随机梯度下降（应用于线性回归、Logistic回归等等）

本文介绍了机器学习中基本的优化算法—梯度下降算法和随机梯度下降算法，以及实际应用到线性回归、Logistic回归、矩阵分解推荐算法等ML中。

梯度下降算法基本公式

常见的符号说明和损失函数

X :所有样本的特征向量组成的矩阵 
x(i) 是第i个样本包含的所有特征组成的向量x(i)=（x(i)1,x(i)2...,x(i)n） 
y(i) 第i个样本的label，每个样本只有一个label，y(i)是标量（一个数值） 
hθ(x(i)) :拟合函数，机器学习中可以用多种类型的拟合函数 
θ 是函数变量，是多个变量的向量 θ=[θ1,θ2,...] 
|hθ(xi)−y(i)| :拟合绝对误差 
求解的目标是使得所有样本点（m个）平均误差最小，即：

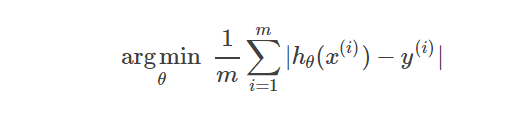
或者平方误差最小，即：

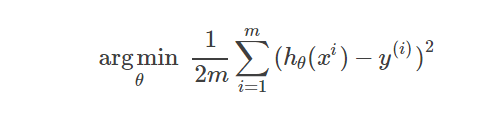
argmin表示使目标函数取最小值时的变量值(即θ）值。

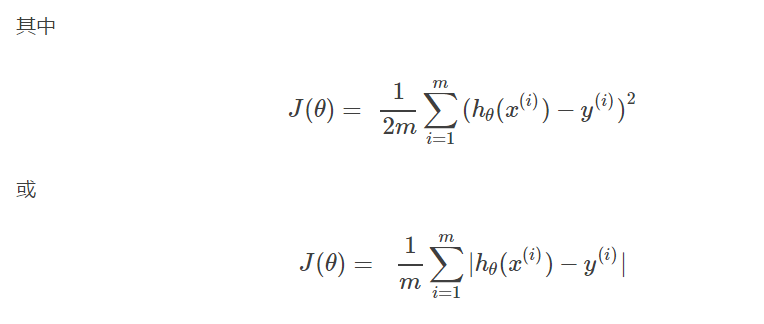
都被称为损失函数（Cost Function） 
J(θ)不只是上面两种形式，不同的机器学习算法可以定义各种其它形式。

梯度下降迭代公式

为了求解θ=[θ1,θ2,...]的值，可以先对其赋一组初值，然后改变θ的值，使得J(θ)最小。函数J(θ)在其负梯度方向下降最快，所以只要使得每个参数θ按函数负梯度方向改变，则J(θ)能最快找到最小值。即

这就是梯度下降算法的迭代公式，其中α表示步长，即往每次下降最快的方向走多远。

线性回归

以多变量线性回归为例： 
拟合函数如下：

Logistic回归

代价函数： 
以Sigmoid函数（Logistic函数）为例说明：

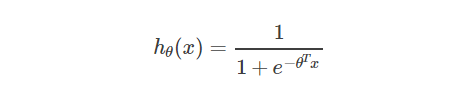
为什么这么定义代价函数呢？我自己通俗理解是，求导后形式简洁，而且： 
y=0，hθ(x)范围为[0，0.5），越接近0.5，代价越高： 
 
由上图可以看出：−log(1−hθ(x(i)))可以很好衡量某一个样本的代价。

y=1时，hθ(x)范围为（0.5，1]，越接近0.5，代价越高： 
 
同样由上图可以看到：−loghθ(x(i))可以很好衡量某一个样本的代价。

迭代更新公式： 
求导过程蛮复杂的，直接给出结果吧:

和线性回归中最后给的更新迭代公式是一模一样的，这也就理解了为什么代价函数设计时比较复杂，还套了log，敢情是为了这？？ 
总之logisitc回归和线性回归最终使用的是一模一样的优化算法。 
还可将这个公式写成用向量来表达的形式：

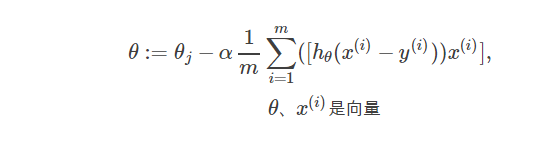
矩阵分解的推荐算法

可以参考我转载的另一篇文章： http://www.cnblogs.com/kobedeshow/p/3651833.html?utm_source=tuicool&utm_medium=referral

随机梯度下降（SGD）

stochastic gradient descent

从梯度上升算法公式可以看出，每次更新回归系数θ时都需要遍历整个数据集。该方法在处理100个左右的数据集尚可，但是如果有数十亿的样本和成千万的特征，这种方法的计算复杂度就太高了。一种改进的方法是一次仅用一个样本点来更新回归系数。由于可以在新样本到来时，对分类器进行增量更新，因此是一个“在线学习”算法，而梯度下降算法一次处理所有的数据被称为“批处理”。更新公式如下：

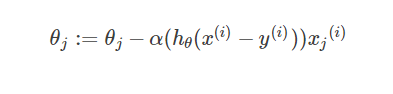
参考文献

（1）Stanford机器学习—第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization 
http://blog.csdn.net/abcjennifer/article/details/7716281?locationNum=2 
（2）机器学习入门：线性回归及梯度下降 
http://blog.csdn.net/xiazdong/article/details/7950084 
（3）梯度下降深入浅出 
http://binhua.info/machinelearning/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B7%B1%E5%85%A5%E6%B5%85%E5%87%BA