Java数据结构和算法（三）：常用排序算法与经典题型

常用的八种排序算法

1.直接插入排序

我们经常会到这样一类排序问题：把新的数据插入到已经排好的数据列中。将第一个数和第二个数排序，然后构成一个有序序列将第三个数插入进去，构成一个新的有序序列。对第四个数、第五个数……直到最后一个数，重复第二步。如题所示：

直接插入排序（Straight Insertion Sorting）的基本思想：在要排序的一组数中，假设前面(n-1) [n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

代码实现：

首先设定插入次数，即循环次数，for(int i=1;i<length;i++)，1个数的那次不用插入。

设定插入数和得到已经排好序列的最后一个数的位数。insertNum和j=i-1。

从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位。

将当前数放置到空着的位置，即j+1。

代码如下：

public void insertSort(int [] a){
        int len=a.length;//单独把数组长度拿出来，提高效率
        int insertNum;//要插入的数
        for(int i=1;i<len;i++){//因为第一次不用，所以从1开始
            insertNum=a[i];
            int j=i-1;//序列元素个数
            while(j>=0&&a[j]>insertNum){//从后往前循环，将大于insertNum的数向后移动
                a[j+1]=a[j];//元素向后移动
                j--;
            }
            a[j+1]=insertNum;//找到位置，插入当前元素
        }
    }

2.希尔排序

针对直接插入排序的下效率问题，有人对次进行了改进与升级，这就是现在的希尔排序。希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

• 插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率
• 但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位

如图所示：

对于直接插入排序问题，数据量巨大时。

将数的个数设为n，取奇数k=n/2，将下标差值为k的数分为一组，构成有序序列。

再取k=k/2 ，将下标差值为k的书分为一组，构成有序序列。

重复第二步，直到k=1执行简单插入排序。

代码实现：

首先确定分的组数。

然后对组中元素进行插入排序。

然后将length/2，重复1,2步，直到length=0为止。

public void sheelSort(int [] a){
        int len=a.length;//单独把数组长度拿出来，提高效率
        while(len!=0){
            len=len/2;
            for(int i=0;i<len;i++){//分组
                for(int j=i+len;j<a.length;j+=len){//元素从第二个开始
                    int k=j-len;//k为有序序列最后一位的位数
                    int temp=a[j];//要插入的元素
                    /*for(;k>=0&&temp<a[k];k-=len){
                        a[k+len]=a[k];
                    }*/
                    while(k>=0&&temp<a[k]){//从后往前遍历
                        a[k+len]=a[k];
                        k-=len;//向后移动len位
                    }
                    a[k+len]=temp;
                }
            }
        }
    }

3.简单选择排序

常用于取序列中最大最小的几个数时。

(如果每次比较都交换，那么就是交换排序；如果每次比较完一个循环再交换，就是简单选择排序。)

遍历整个序列，将最小的数放在最前面。

遍历剩下的序列，将最小的数放在最前面。

重复第二步，直到只剩下一个数。

代码实现：

首先确定循环次数，并且记住当前数字和当前位置。

将当前位置后面所有的数与当前数字进行对比，小数赋值给key，并记住小数的位置。

比对完成后，将最小的值与第一个数的值交换。

重复2、3步。

public void selectSort(int[]a){
        int len=a.length;
        for(int i=0;i<len;i++){//循环次数
            int value=a[i];
            int position=i;
            for(int j=i+1;j<len;j++){//找到最小的值和位置
                if(a[j]<value){
                    value=a[j];
                    position=j;
                }
            }
            a[position]=a[i];//进行交换
            a[i]=value;
        }
    }

4.堆排序

对简单选择排序的优化。

将序列构建成大顶堆。

将根节点与最后一个节点交换，然后断开最后一个节点。

重复第一、二步，直到所有节点断开。

代码如下：

public  void heapSort(int[] a){
           int len=a.length;
           //循环建堆
           for(int i=0;i<len-1;i++){
               //建堆
               buildMaxHeap(a,len-1-i);
               //交换堆顶和最后一个元素
               swap(a,0,len-1-i);
           }
       }
        //交换方法
       private  void swap(int[] data, int i, int j) {
           int tmp=data[i];
           data[i]=data[j];
           data[j]=tmp;
       }
       //对data数组从0到lastIndex建大顶堆
       private void buildMaxHeap(int[] data, int lastIndex) {
           //从lastIndex处节点（最后一个节点）的父节点开始
           for(int i=(lastIndex-1)/2;i>=0;i--){
               //k保存正在判断的节点
               int k=i;
               //如果当前k节点的子节点存在
               while(k*2+1<=lastIndex){
                   //k节点的左子节点的索引
                   int biggerIndex=2*k+1;
                   //如果biggerIndex小于lastIndex，即biggerIndex+1代表的k节点的右子节点存在
                   if(biggerIndex<lastIndex){
                       //若果右子节点的值较大
                       if(data[biggerIndex]<data[biggerIndex+1]){
                           //biggerIndex总是记录较大子节点的索引
                           biggerIndex++;
                       }
                   }
                   //如果k节点的值小于其较大的子节点的值
                   if(data[k]<data[biggerIndex]){
                       //交换他们
                       swap(data,k,biggerIndex);
                       //将biggerIndex赋予k，开始while循环的下一次循环，重新保证k节点的值大于其左右子节点的值
                       k=biggerIndex;
                   }else{
                       break;
                   }
               }
           }
       }

5.冒泡排序

很简单，用到的很少，据了解，面试的时候问的比较多！

将序列中所有元素两两比较，将最大的放在最后面。

将剩余序列中所有元素两两比较，将最大的放在最后面。

重复第二步，直到只剩下一个数。

代码实现：

设置循环次数。

设置开始比较的位数，和结束的位数。

两两比较，将最小的放到前面去。

重复2、3步，直到循环次数完毕。

public void bubbleSort(int []a){
           int len=a.length;
           for(int i=0;i<len;i++){
               for(int j=0;j<len-i-1;j++){//注意第二重循环的条件
                   if(a[j]>a[j+1]){
                       int temp=a[j];
                       a[j]=a[j+1];
                       a[j+1]=temp;
                   }
               }
           }
       }

6.快速排序

要求时间最快时。

选择第一个数为p，小于p的数放在左边，大于p的数放在右边。

递归的将p左边和右边的数都按照第一步进行，直到不能递归。

public void quickSort(int[]a,int start,int end){
           if(start<end){
               int baseNum=a[start];//选基准值
               int midNum;//记录中间值
               int i=start;
               int j=end;
               do{
                   while((a[i]<baseNum)&&i<end){
                       i++;
                   }
                   while((a[j]>baseNum)&&j>start){
                       j--;
                   }
                   if(i<=j){
                       midNum=a[i];
                       a[i]=a[j];
                       a[j]=midNum;
                       i++;
                       j--;
                   }
               }while(i<=j);
                if(start<j){
                    quickSort(a,start,j);
                }
                if(end>i){
                    quickSort(a,i,end);
                }
           }
       }

7.归并排序

速度仅次于快速排序，内存少的时候使用，可以进行并行计算的时候使用。

选择相邻两个数组成一个有序序列。

选择相邻的两个有序序列组成一个有序序列。

重复第二步，直到全部组成一个有序序列。

public  void mergeSort(int[] a, int left, int right) {
           int t = 1;// 每组元素个数
           int size = right - left + 1;
           while (t < size) {
               int s = t;// 本次循环每组元素个数
               t = 2 * s;
               int i = left;
               while (i + (t - 1) < size) {
                   merge(a, i, i + (s - 1), i + (t - 1));
                   i += t;
               }
               if (i + (s - 1) < right)
                   merge(a, i, i + (s - 1), right);
           }
        }  

        private static void merge(int[] data, int p, int q, int r) {
           int[] B = new int[data.length];
           int s = p;
           int t = q + 1;
           int k = p;
           while (s <= q && t <= r) {
               if (data[s] <= data[t]) {
                   B[k] = data[s];
                   s++;
               } else {
                   B[k] = data[t];
                   t++;
               }
               k++;
           }
           if (s == q + 1)
               B[k++] = data[t++];
           else
               B[k++] = data[s++];
           for (int i = p; i <= r; i++)
               data[i] = B[i];
        }

8.基数排序

用于大量数，很长的数进行排序时。

将所有的数的个位数取出，按照个位数进行排序，构成一个序列。

将新构成的所有的数的十位数取出，按照十位数进行排序，构成一个序列。

代码实现：

public void baseSort(int[] a) {
               //首先确定排序的趟数;
               int max = a[0];
               for (int i = 1; i < a.length; i++) {
                   if (a[i] > max) {
                       max = a[i];
                   }
               }
               int time = 0;
               //判断位数;
               while (max > 0) {
                   max /= 10;
                   time++;
               }
               //建立10个队列;
               List<ArrayList<Integer>> queue = new ArrayList<ArrayList<Integer>>();
               for (int i = 0; i < 10; i++) {
                   ArrayList<Integer> queue1 = new ArrayList<Integer>();
                   queue.add(queue1);
               }
               //进行time次分配和收集;
               for (int i = 0; i < time; i++) {
                   //分配数组元素;
                   for (int j = 0; j < a.length; j++) {
                       //得到数字的第time+1位数;
                       int x = a[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
                       ArrayList<Integer> queue2 = queue.get(x);
                       queue2.add(a[j]);
                       queue.set(x, queue2);
                   }
                   int count = 0;//元素计数器;
                   //收集队列元素;
                   for (int k = 0; k < 10; k++) {
                       while (queue.get(k).size() > 0) {
                           ArrayList<Integer> queue3 = queue.get(k);
                           a[count] = queue3.get(0);
                           queue3.remove(0);
                           count++;
                       }
                   }
               }
        }

新建测试类进行测试

public class TestSort {
    public static void main(String[] args) {
        int []a=new int[10];
        for(int i=1;i<a.length;i++){
            //a[i]=(int)(new Random().nextInt(100));
            a[i]=(int)(Math.random()*100);
        }
        System.out.println("排序前的数组为："+Arrays.toString(a));
        Sort s=new Sort();
        //排序方法测试
        //s.insertSort(a);
        //s.sheelSort(a);
        //s.selectSort(a);
        //s.heapSort(a);
        //s.bubbleSort(a);
        //s.quickSort(a, 1, 9);
        //s.mergeSort(a, 3, 7);
        s.baseSort(a);
        System.out.println("排序后的数组为："+Arrays.toString(a));
    }

}

部分结果如下:

9.桶排序（Bucket Sort）

　　要使桶排序正常运行，需要额外的信息：

　　输入A₁，A₂，...，A_N必须只由小于M的正整数构成，即A_i<M。使用一个大小为M的数组result，初始化为全0。数组有M个单元，即M个桶（bucket）。

public static void bucketSort(int[] a){
        //常用写法
        int max = Integer.MIN_VALUE;
        for (int i =0;i<a.length;i++){
            max = Math.max(max,a[i]);
        }

        int[] bucket = new int[max+1];// 定义桶数组，这个数组的特征是长度是排序数组的最大值+1，为什么要+1？因为不+1桶数组最后一位会下标越界

        for (int i =0;i<a.length;i++){
            //桶数组此下标有数据，数值就加一
            bucket[a[i]]++;
        }

        int i = 0;

        for (int j = 0;j<bucket.length;j++){
            while (bucket[j]-->0){
                a[i++]=j;
            }
        }
    }

步骤：

　　result[Ai]中存放的是Ai出现的次数；

读入Ai时，result[Ai]增1；　　

　　所有输入数据读入后，扫描数组result，打印出排序后的数据，result[Ai]值是n，Ai就打印n次.

eg.

输入数组{1,4,5,3,7,8,4,9,6,5,0}，最大为9，另建一个大小为10的数组，初始化为全0。

读入数组：

　　遇到1，将result[1]加1

　　遇到4，将result[4]加1

　　......

　　遇到5，将result[5]加1

　　遇到0，将result[0]加1

得到结果：

　　

打印结果：

　　0 1 3 4 4 5 5 6 7 8 9

时间复杂度：

　　算法用时O(M+N)，M为桶的个数，N为待排序数组的大小。

空间复杂度：

　　O(M+N)

如果输入数据非常庞大，桶的数量会非常多，空间代价将会非常大。　

如果要进行比较可已加入时间，输出排序时间，从而比较各个排序算法的优缺点，这里不再做介绍。

总结：

一、稳定性:

　   稳定：冒泡排序、插入排序、归并排序和基数排序

　　不稳定：选择排序、快速排序、希尔排序、堆排序

二、平均时间复杂度

　　O(n^2):直接插入排序，简单选择排序，冒泡排序。

　　在数据规模较小时（9W内），直接插入排序，简单选择排序差不多。当数据较大时，冒泡排序算法的时间代价最高。性能为O(n^2)的算法基本上是相邻元素进行比较，基本上都是稳定的。

　　O(nlogn):快速排序，归并排序，希尔排序，堆排序。

　　其中，快排是最好的， 其次是归并和希尔，堆排序在数据量很大时效果明显。

三、排序算法的选择

　　1.数据规模较小

　　（1）待排序列基本序的情况下，可以选择直接插入排序；

　　（2）对稳定性不作要求宜用简单选择排序，对稳定性有要求宜用插入或冒泡

　　2.数据规模不是很大

　　（1）完全可以用内存空间，序列杂乱无序，对稳定性没有要求，快速排序，此时要付出log（N）的额外空间。

　　（2）序列本身可能有序，对稳定性有要求，空间允许下，宜用归并排序

　　3.数据规模很大

　　（1）对稳定性有求，则可考虑归并排序。

　　（2）对稳定性没要求，宜用堆排序

　　4.序列初始基本有序（正序），宜用直接插入，冒泡

各算法复杂度如下：

排序算法经典题

三色排序

问题描述

输入一个整型数组，每个元素在0~2之间，其中0，1，2分别代表红、白、蓝。现要求对数组进行排序，相同颜色的在一起，而且按红白蓝顺序先后排列。要求时间复杂度为O(n)。

问题分析

最容易想到的是排序，比如快排，归并，堆排等，但它们的时间复杂度为O(nlogn)，与题意不符。

第二种想到的是计数排序，扫描一遍过去，分别记录0，1，2的个数，然后再对数组进行赋值。时间复杂度为O(2n)，即O(n)，满足条件。

还有一种方法，只需扫描一遍数组即可，其充分利用了元素只有3种的特性：在扫描数组的时候，使用首尾俩个指针，分别指示0、1与1、2边界。比如源数组为{2， 2， 0， 0， 1， 1  }。

第一步：首指针p0，尾指针p1，i标识当前扫描位置，当前位置值为2，需要将其交换至尾指针p1位置，p1要向前移动一位，p0、i位置不变。

第二步：i位置值不为0、2，i要向后移动一位，p0、p1位置不变。

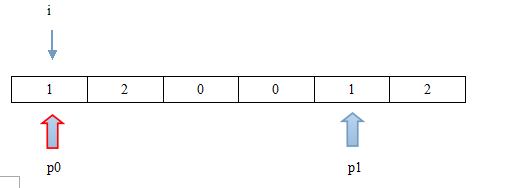
第三步：i位置值为2，需要将其交换至尾指针p1位置，并且p1往前移动一位，i与p0位置不变。

第四步：i位置不为0、2，i要向后移动一位，p0、p1位置不变。

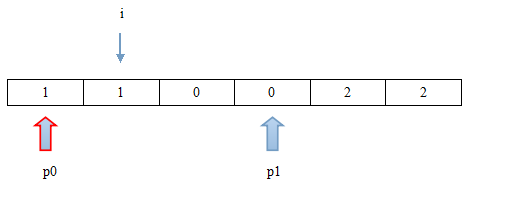
第五步：i位置值为0，需要将其交换至首指针p0位置，并且p0往后移动一位，i与p1位置不变。

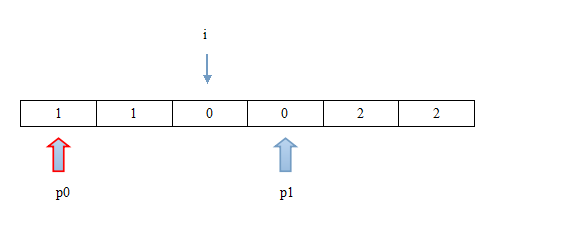
第六步：i位置不为0、2，i要向后移动一位，p0、p1位置不变。

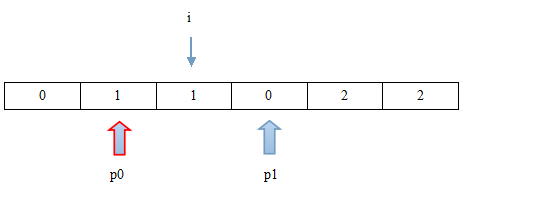
第七步：i位置值为0，需要将其交换至首指针p0位置，并且p0往后移动一位，i与p1位置不变。

第八步：i位置不为0、2，i要向后移动一位，p0、p1位置不变。

第九步：i位置超过p1位置了，结束。

实现代码

public static void sss(int[] a){
//        输入一个整型数组，每个元素在0~2之间，其中0，1，2分别代表红、白、蓝。
//        现要求对数组进行排序，相同颜色的在一起，而且按红白蓝顺序先后排列。要求时间复杂度为O(n)。
//        若为2，值移到尾指针p1，p0和i不变，p1前移一位
//        若为1，i后移一位，p0和p1不变
//        若为0，值移到首指针p0，p1和i不变，p0后移一位，
        int len = a.length;
        int p0 = 0;// 首指针
        int p1 = len-1;// 尾指针
        int i= 0;// 当前位置
        int value;// 当前位置的值
        while(true) {

            value = a[i];

            if (i>p1) {
                break;
            }

            if (value==0) {
                a[i]=a[p0];
                a[p0]=value;
                p0++;
            }else if (value==1) {
                i++;
//                value=a[index];
            }else if (value==2) {
                a[i]=a[p1];
                a[p1] = value;
                p1--;
            }

        }

    }

有序矩阵查找

题目：现在有一个行和列都排好序的矩阵，请设计一个高效算法，快速查找矩阵中是否含有值x。给定一个int矩阵mat，同时给定矩阵大小nxm及待查找的数x，请返回一个bool值，代表矩阵中是否存在x。所有矩阵中数字及x均为int范围内整数。保证n和m均小于等于1000。测试样例：[[1,2,3],[4,5,6],[7,8,9]],3,3,10返回：false

思路：等同于Array1: 二维数组中的查找。常识二维数组的写法不要忘记。已知每一行是有序的，每一列也是有序的，最直接的思路是对全部元素进行遍历，时间复杂度显然是O(n*m)；这里要利用每行每列有序这个特性来简化问题，从右上角元素开始遍历，如果结点x>a[0,m-1]，说明x不在结点这一行中，于是下一次从a[1,m-1]元素进行比较；如果x<a[0,m-1]，说明x不在结点这一列中，于是从a[0,m-2]结点开始遍历，即通过将x与当前矩阵的右上角a[p,q]元素进行比较，如果x小，那么排除右上角结点所在列，即对q--;如果x大，那么排除右上角结点所在行，即进行p++,直到p>n-1或者q<0时结束。这样的时间复杂度是O(n+m)

即最多只需要与n+m个结点进行比较即可作出判断。

实现代码

/**
     * 有序矩阵查找
     * @param a
     * @param x 要比较的数
     */
    public static boolean sss(int[][] a,int x){
        int ni = 0;// 横坐标下标
        int mi = m-1;// 纵坐标下标
        int t = 0;
        boolean result = true;
//        int test = 0;
        while (true) {

//            System.out.println("测试需要循环几次："+(++test));

            if (ni>mi) {
                result = false;
                break;
            }

            if (x>a[ni][mi]) {
                ni++;
            }else if(x<a[ni][mi]){
                mi--;
            }else{
                // 相等直接返回
                break;
            }
        }

        return result;

    }

需要排序的最短子数组

题目

对于一个数组，请设计一个高效算法计算需要排序的最短子数组的长度。
给定一个int数组A和数组的大小n，请返回一个二元组，代表所求序列的长度。(原序列位置从0开始标号,若原序列有序，返回0)。保证A中元素均为正整数。

测试样例：[1,4,6,5,9,10],6
返回：2

思路

从左开始遍历数组，记录下已经遍历部分的最大值max，如果遍历的数值小于max时，记录这种情况下最右的位置right。

从左开始遍历数组，记录下已经遍历部分的最大值min，如果遍历的数值大于min时，记录这种情况下最右的位置left。

代码实现

public int shortestSubsequence(int[] A, int n) {
        int max=A[0],min=A[n-1];
        int right=0,left=0;
        for(int i=0;i<n;i++){
            max=Math.max(max,A[i]);
            if(A[i]<max){
                right=i;
            }
        }

        for(int i=n-1;i>=0;i--){
            min=Math.min(min,A[i]);
            if(A[i]>min){
                left=i;
            }
        }

        return right==left?0:right-left+1;
    }

排序数组中的相邻两数最大差值

题目

给定一个数组A及其大小n，求其排序后的相邻两数的最大差值。（注：要求时间复杂度为O(n)）

思路

题目要求对排序后的数组进行操作，显然需要先对数组进行排序。如果没有要求时间复杂度，那么可以有很多种排序算法，如快速排序、堆排序、归并排序等等。但是这里要求时间复杂度为O(n)，就不能用上述常规的排序算法了。

那么桶排序可以吗？由于我们不知道最大数的位数，因此，如果最大数的位数很大的话，我们就需要成千上万个桶，显然对空间要求太大。我们可以利用桶排序的思想，利用它的变种：

1) 首先求出数组的最大值max和最小值min；

2) 然后将该区间均等的划分为n+1份，即n+1个桶，那么由于只有n个数，因此，必定至少有一个桶为空桶；

3) 遍历数组，将所有数入桶，并记录每一个桶的最大值和最小值；

4) 不用考虑桶内数的差值，因为它都不会大过空桶两边的桶的数的差值；

5) 依次遍历每一个桶，找到一个空桶，记录其前一个非空桶的最大值和其后一个非空桶的最小值，它们的差值就是最大的（考虑有多个空桶的情况）。

代码实现

public static int maxGap(int[] nums) {
        if (nums == null || nums.length < 2) {
            return 0;
        }
        int len = nums.length;
        int min = Integer.MAX_VALUE;
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < len; i++) {
            min = Math.min(min, nums[i]);
            max = Math.max(max, nums[i]);
        }
        if (min == max) {
            return 0;
        }
        boolean[] hasNum = new boolean[len + 1];
        int[] maxs = new int[len + 1];
        int[] mins = new int[len + 1];
        int bid = 0;
        for (int i = 0; i < len; i++) {
            bid = bucket(nums[i], len, min, max); // 算出桶号
            mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i];
            maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i];
            hasNum[bid] = true;
        }
        int res = 0;
        int lastMax = 0;
        int i = 0;
        while (i <= len) {
            if (hasNum[i++]) { //找到第一个不为空的桶
                lastMax = maxs[i - 1];
                break;
            }
        }
        for (; i <= len; i++) {
            if (hasNum[i]) {
                res = Math.max(res, mins[i] - lastMax);
                lastMax = maxs[i];
            }
        }
        return res;
    }
     //使用long类型是为了防止相乘时溢出
    public static int bucket(long num, long len, long min, long max) {
        return (int) ((num - min) * len / (max - min));
    }

有序数组合并

题目

有两个从小到大排序以后的数组A和B，其中A的末端有足够的缓冲空格容纳B。请编写一个方法将B合并入A并排序。

给定两个有序int数组A和B，其中A的缓冲空用0填充，同时给定A和B的真实大小int m和int n，请返回合并后的数组。

解法一：

从结尾开始归并，不会覆盖元素。从A[n+m-1]处开始往前一个元素一个元素的求，每次都要比较A[i]和B[j]的大小。

需要注意的是，要考虑到： A和B有一个为空时的情况

public static void merge(int[] a,int[] b,int m,int n){
    int i , j , k ;
        for( i = m - 1, j = n - 1, k = n + m -1; k >= 0; k--){
            if( i >= 0 &&(j < 0 || a[i] >= b[j]) )
                a[k] = a[i--];
            else
                a[k] = b[j--];
        }
}

解法二：

算法思想是：由于合并后A数组的大小必定是m+n，所以从最后面开始往前赋值，先比较A和B中最后一个元素的大小，把较大的那个插入到m+n-1的位置上，再依次向前推。如果A中所有的元素都比B小，那么前m个还是A原来的内容，没有改变。如果A中的数组比B大的，当A循环完了，B中还有元素没加入A，直接用个循环把B中所有的元素覆盖到A剩下的位置。代码如下:

public static void merge(int[] a,int[] b,int m,int n){
        int count = m + n - 1;
        --m; --n;
        while (m >= 0 && n >= 0) a[count--] = a[m] > b[n] ? a[m--] : b[n--];
        while (n >= 0) a[count--] = b[n--];
}

测试

public static void main(String[] args) {
        int[] a = new int[]{1,4,7,16,25,27,0,0,0,0,0};
        int[] b = new int[]{3,4,8,11,20};
        merge(a, b, 6, 5);
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i]+"\t");
        }
    }

未完