洛谷 P4072 [SDOI2016]征途斜率优化DP

题目描述

$Pine$ 开始了从 $S$ 地到 $T$ 地的征途。

从$S$地到$T$地的路可以划分成 $n$ 段，相邻两段路的分界点设有休息站。

$Pine$计划用$m$天到达$T$地。除第$m$天外，每一天晚上$Pine$都必须在休息站过夜。所以，一段路必须在同一天中走完。

$Pine$希望每一天走的路长度尽可能相近，所以他希望每一天走的路的长度的方差尽可能小。

帮助$Pine$求出最小方差是多少。

设方差是$v$，可以证明，$v\times m^2$是一个整数。为了避免精度误差，输出结果时输出$v\times m^2$。

输入格式

第一行两个数 $n$、$m$。

第二行 $n$ 个数，表示 $n$ 段路的长度

输出格式

一个数，最小方差乘以 $m^2$ 后的值

输入输出样例

输入 #1

5 2

1 2 5 8 6

输出 #1

36

说明/提示

对于 $30\%$ 的数据，$1 \le n \le 10$

对于 $60\%$ 的数据，$1 \le n \le 100$

对于 $100\%$ 的数据，$1 \le n \le 3000$

保证从 $S$ 到 $T$ 的总路程不超过 $30000$ 。

分析

\[s^2 \times m^2=\frac{(v_1-\overline{v})^2+(v_2-\overline{v})^2+...+(v_m-\overline{v})^2}m \times m^2
\]

\[s^2 \times m^2=((v_1-\overline{v})^2+(v_2-\overline{v})^2+...+(v_m-\overline{v})^2) \times m
\]

\[s^2 \times m^2=m\times \sum_{i=1}^mv_i^2+m^2 \times \overline {v}^2-2\times m \times \overline {v} \times sum[n]
\]

又因为$$\overline{v}=\frac{sum[n]}{m}$$

所以

\[s^2\times m^2=m\times \sum_{i=1}^mv_i^2-sum[n]\times sum[n]
\]

后面的值是固定的，所以我们只需要让前面的值最小化即可

我们设$f[i][j]$为前$i$天分成$j$段所得到的最小值

那么就有

\[f[i][k]=\min(f[j][k-1]+(sum[i]-sum[j])^2)
\]

展开就有

\[f[i][k]=f[j][k-1]+sum[i]^2+sum[j]^2-2\times sum[i] \times sum[j]
\]

移项得

\[f[j][k-1]+sum[j]^2=2\times sum[i] \times sum[j]+f[i][k]-sum[i]^2
\]

可以用斜率优化

我们把$f[j][k-1]+sum[j]^2$看成$y$

把$2 \times sum[i]$看成$k$

把$sum[j]$看成$x$

把$f[i][k]-sum[i]^2$看成$b$

这样，对于每一个$i$来说，直线的$k$是确定的

我们要使$f[i][k]$最小，也就是要使$b$最小

我们可以把所有的$j$想象成空间中的点

知道了斜率，知道了直线上的点，那么这条直线就确定了

那么我们考虑什么样的点使直线的$b$最大

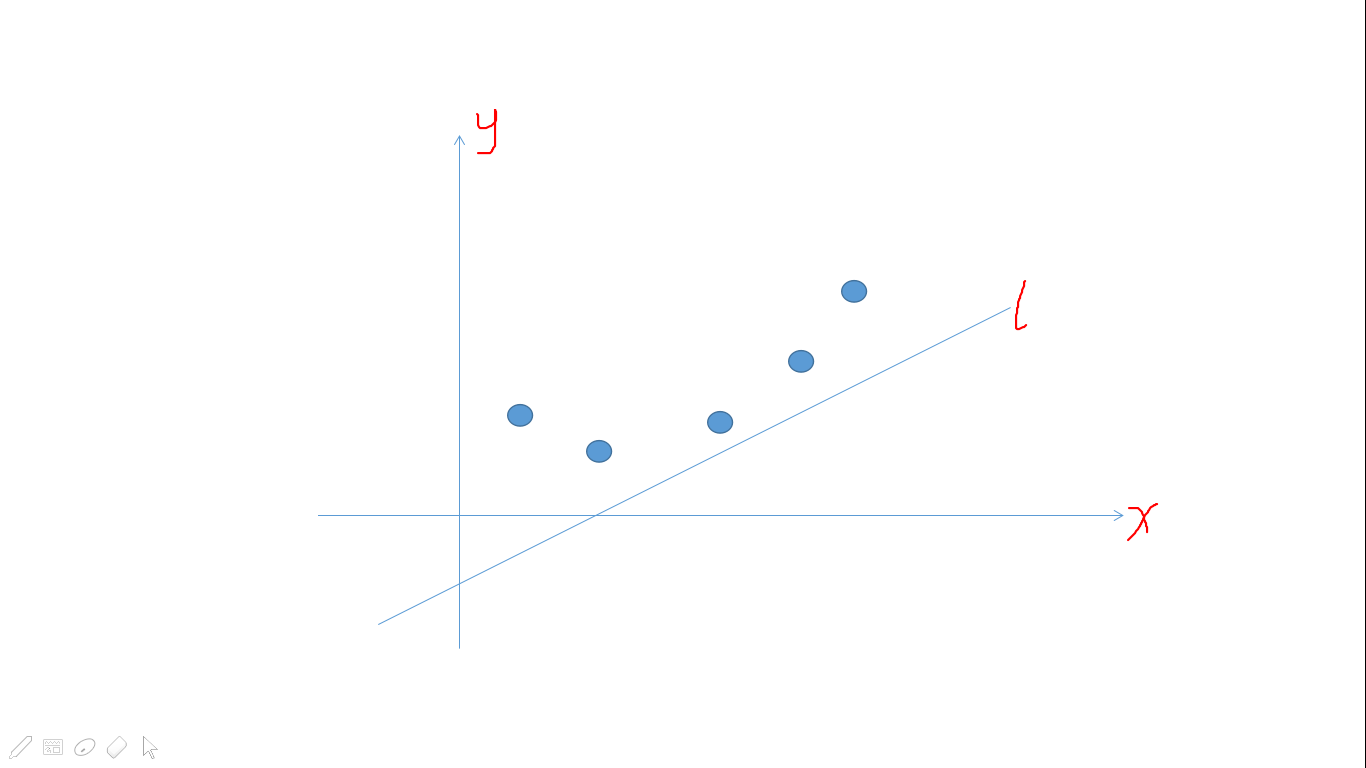
直线$l$是我们要移动的直线，平面中的点是可以转移的$j$值

我们会发现当当前点和后一个点形成的直线的斜率恰好大于直线$l$的斜率是，由当前点转移决策是最优的

这就是代码里面的

while(head<tail && xl(q[head],q[head+1])<2*sum[j]) head++;

f[j]=g[q[head]]+sum[j]*sum[j]+sum[q[head]]*sum[q[head]]-2*sum[j]*sum[q[head]];

我们再去考虑什么样的点肯定不会对结果产生贡献

上面的图中$2$号节点是无论如何也不会更新其它节点的

因为$1$号节点或$3$号节点总会比它更优

这就是代码里的

 while(head<tail && xl(q[tail-1],q[tail])>=xl(q[tail],i)) tail--;

整个过程就相当于维护了一个下凸包

但是，如果斜率不是单调递增，我们就不能从前面清空队列直接转移，只能二分答案

比如上面这幅图如果我们一直从前清空队列的话那么就会把$2$号决策点弹出队列

但是如果之后遇到一个斜率比较小的直线$m$那么就不能转移到最优解

代码

#include<cstdio>

#include<cstring>

inline int read(){

	int x=0,fh=1;

	char ch=getchar();

	while(ch<'0' || ch>'9'){

		if(ch=='-') fh=-1;

		ch=getchar();

	}

	while(ch>='0' && ch<='9'){

		x=(x<<1)+(x<<3)+(ch^48);

		ch=getchar();

	}

	return x*fh;

}

const int maxn=1e6+5;

int a[maxn],sum[maxn],n,m,f[maxn],g[maxn],q[maxn],head,tail;

double xl(int i,int j){

	return (double)(g[i]+sum[i]*sum[i]-g[j]-sum[j]*sum[j])/(double)(sum[i]-sum[j]);

}

int main(){

	n=read(),m=read();

	for(int i=1;i<=n;i++){

		a[i]=read();

		sum[i]=sum[i-1]+a[i];

		g[i]=sum[i]*sum[i];

	}

	for(int i=1;i<m;i++){

		head=tail=1;

		q[1]=i;

		for(int j=i+1;j<=n;j++){

			while(head<tail && xl(q[head],q[head+1])<2*sum[j]) head++;

			f[j]=g[q[head]]+sum[j]*sum[j]+sum[q[head]]*sum[q[head]]-2*sum[j]*sum[q[head]];

			while(head<tail && xl(q[tail],q[tail-1])>xl(q[tail-1],j)) tail--;

			q[++tail]=j;

		}

		for(int j=1;j<=n;j++) g[j]=f[j];

	}

	printf("%d\n",f[n]*m-sum[n]*sum[n]);

	return 0;

}