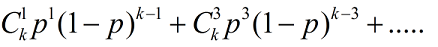【非原创】LightOJ - 1284 Lights inside 3D Grid【概率期望】
学习博客:
题意:
在一个三维的空间,每个点都有一盏灯,开始全是关的,
现在每次随机选两个点,把两个点之间的全部点,开关都按一遍;问k次过后开着的灯的期望数量;
题解:
肯定不能从随机抽取两个数这里入手的,要求开着的灯的数量就从对每一盏灯,操作结束后灯开着的概率,然后将这些概率求和就是对于整个矩阵到最后开着的灯的数量了,这就把矩阵的问题落实到了对于求每个坐标的概率的问题。
对每个点单独计算贡献,即k次过后每个点开关被按了奇数次的期望
一个点如果被包到所选空间里,那么说明选的两个点,x坐标在这个点两侧,y坐标在这个点两侧,z坐标在这个点两侧;
对于一维的,可以用求出两个点在x这一点两侧的概率。然后三维的只要当成三个一维的乘起来就行了。
E=
求法:
代码(亦非原创):
1 #include<bits/stdc++.h>
2
3 using namespace std;
4
5 int t,x,y,z,m;
6
7 int main()
8
9 {
10
11 scanf("%d",&t);
12
13 int cas=0;
14
15 while(t--)
16
17 {
18
19 scanf("%d%d%d%d",&x,&y,&z,&m);
20
21 double ans=0.0;
22
23 for(int i=1;i<=x;i++)
24
25 for(int j=1;j<=y;j++)
26
27 for(int k=1;k<=z;k++)
28
29 {
30
31 double p=0.0;
32
33 p= 1.0-1.0*((x-i)*(x-i)+(i-1)*(i-1))/(x*x);
34
35 p*=1.0-1.0*((y-j)*(y-j)+(j-1)*(j-1))/(y*y);
36
37 p*=1.0-1.0*((z-k)*(z-k)+(k-1)*(k-1))/(z*z);
38
39
40
41 ans+=0.5-0.5*pow(1.0-2*p,1.0*m);
42
43 }
44
45 printf("Case %d: %.11lf\n",++cas,ans);
46
47 }
48
49 return 0;
50
51 }
【非原创】LightOJ - 1284 Lights inside 3D Grid【概率期望】的更多相关文章
- LightOJ 1284 - Lights inside 3D Grid 概率/期望/二项式定理
题意:给你一个长宽高为x,y,z的长方体,里面每个格子放了灯,再给你k次选取任意长方体形状的区块,对其内所有灯开或关操作,初始为关,问亮灯数量的期望值. 题解:首先考虑选取区块的概率,使某个灯在被选取 ...
- LightOJ 1284 Lights inside 3D Grid (数学期望)
题意:在一个三维的空间,每个点都有一盏灯,开始全是关的.现在每次随机选两个点,把两个点之间的全部点,开关都按一遍,问k次过后开着的灯的期望数量: 析:很容易知道,如果一盏灯被按了奇数次,那么它肯定是开 ...
- LightOJ - 1284 Lights inside 3D Grid —— 期望
题目链接:https://vjudge.net/problem/LightOJ-1284 1284 - Lights inside 3D Grid PDF (English) Statistic ...
- LightOJ - 1284 Lights inside 3D Grid (概率计算)
题面: You are given a 3D grid, which has dimensions X, Y and Z. Each of the X x Y x Z cells contains a ...
- LightOJ1284 Lights inside 3D Grid (概率DP)
You are given a 3D grid, which has dimensions X, Y and Z. Each of the X x Y x Z cells contains a lig ...
- Lights inside 3D Grid LightOJ - 1284 (概率dp + 推导)
Lights inside 3D Grid LightOJ - 1284 题意: 在一个三维的空间,每个点都有一盏灯,开始全是关的, 现在每次随机选两个点,把两个点之间的全部点,开关都按一遍:问k次过 ...
- LightOj_1284 Lights inside 3D Grid
题目链接 题意: 给一个X * Y * Z 的立方体, 每个单位立方体内都有一盏灯, 初始状态是灭的, 你每次操作如下: 1)选择一个点(x1, y1, z1) 再选择一个点(x2, y2, ...
- uva 11605 - Lights inside a 3d Grid(概率)
option=com_onlinejudge&Itemid=8&page=show_problem&problem=2652" style=""& ...
- 3D Grid Effect – 使用 CSS3 制作网格动画效果
今天我们想与大家分享一个小的动画概念.这个梦幻般的效果是在马库斯·埃克特的原型应用程序里发现的.实现的基本思路是对网格项目进行 3D 旋转,扩展成全屏,并呈现内容.我们试图模仿应用程序的行为,因此 ...
随机推荐
- 记录Js动态加载页面.append、html、appendChild、repend添加元素节点不生效以及解决办法
今天再优化blog页面的时候添加了个关注按钮和图片,但是页面上这个按钮和图片时有时无,本来是搞后端的,被这个前端的小问题搞得抓耳挠腮的! 网上各种查询解决方案,把我解决问题的艰辛历程分享出来,希望大家 ...
- 24V降压3.3V芯片,低压降线性稳压器
PW6206系列是一款高精度,高输入电压,低静态电流,高速,低压降线性稳压器具有高纹波抑制.在VOUT=5V&VIN=7V时,输入电压高达40V,负载电流高达300mA,采用BCD工艺制造.P ...
- JavaScript中创建对象的三种方式!
JavaScript中创建对象的三种方式! 第一种 利用对象字面量! // 创建对象的三种方式! // 1 对象字面量. var obj = { // 对象的属性和方法! name: 'lvhang' ...
- LoadRunner监控Centos和Ubuntu资源之服务器配置
Centos 我用的版本是Centos6.8 首先更新源以及基础操作我就不说了,直接上步骤: Step 1 安装相关程序 执行命令:yum install inetd,这一步是为了安装rstatd ...
- Jmeter的Cookie管理器调试与参数化
默认系统都是需要登录,才能操作其它接口,所以需要添加一个HTTP Cookie 管理器,默认Cookie管理器是关闭的,需要修改jmeter配置文件jmeter.properties,该文件在jme ...
- C#高级编程第11版 - 第六章 索引
[1]6.2 运算符 1.&符在C#里是逻辑与运算.管道符号|在C#里则是逻辑或运算.%运算符用来返回除法运算的余数,因此当x=7时,x%5的值将是2. [2]6.2.1 运算符的简写 1.下 ...
- 逃逸分析与栈、堆分配分析 escape_analysis
小结: 1.当形参为 interface 类型时,在编译阶段编译器无法确定其具体的类型.因此会产生逃逸,最终分配到堆上. 2.The construction of a value doesn't d ...
- OSS与文件系统的对比 文件存储 块存储 对象存储
基本概念介绍_开发指南_对象存储 OSS-阿里云 https://help.aliyun.com/document_detail/31827.html 强一致性 Object 操作在 OSS 上具有 ...
- how2j 仿天猫j2EE零散笔记
1. 在servlet中拼接 :"http://localhost:8080/tmall/admin_property_list?cid=83" 这句话中的cid=83时, c ...
- Vue技术点整理-Vuex
什么是Vuex? 1,Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式.它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化 2,每一个 Vuex ...