力扣561. 数组拆分 I-C语言实现-简单题

题目

传送门

给定长度为 2n 的整数数组 nums ，你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ，使得从 1 到 n 的 min(ai, bi) 总和最大。

返回该 最大总和 。

示例 1：

输入：nums = [1,4,3,2]

输出：4

解释：所有可能的分法（忽略元素顺序）为：

1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
   
   所以最大总和为 4

示例 2：

输入：nums = [6,2,6,5,1,2]

输出：9

解释：最优的分法为 (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9

提示：

1 <= n <= 104
nums.length == 2 * n
-104 <= nums[i] <= 104

来源：力扣（LeetCode）

解题

模板

int arrayPairSum(int* nums, int numsSize){

}

分析

这里的题目不难，所要思考的是我们对于这个两两分组最小值之和怎样取得最大值。

结果就是尽可能大的和大的一组，使得至少有一个大的进入最后的综合计算，大的数据进入越多就越大，其实也可以理解未计算第二大，第四大，第六大的元素之和，即求取偶数按大小排名元素之和。既然如此我们就可以选择一种新的解决办法，进行排序然后对于偶数项相加就可以得到最后的答案。

第一版 实现办法：

int arrayPairSum(int* nums, int numsSize){
    int x=0,ret=0;
    for(int i=0;i<numsSize;i++){
        for(int k=i;k<numsSize;k++){
            if(nums[i]<nums[k]){
                x=nums[i];
                nums[i]=nums[k];
                nums[k]=x;
            }
        }
    }
    for(int i=0;i<numsSize;i+=2){
        ret+=nums[i];
    }
    return ret;
}

这个代码有问题吗？没有，但是他有一个缺点，复杂度使整个程序运行比较多个变量的数组就会超时

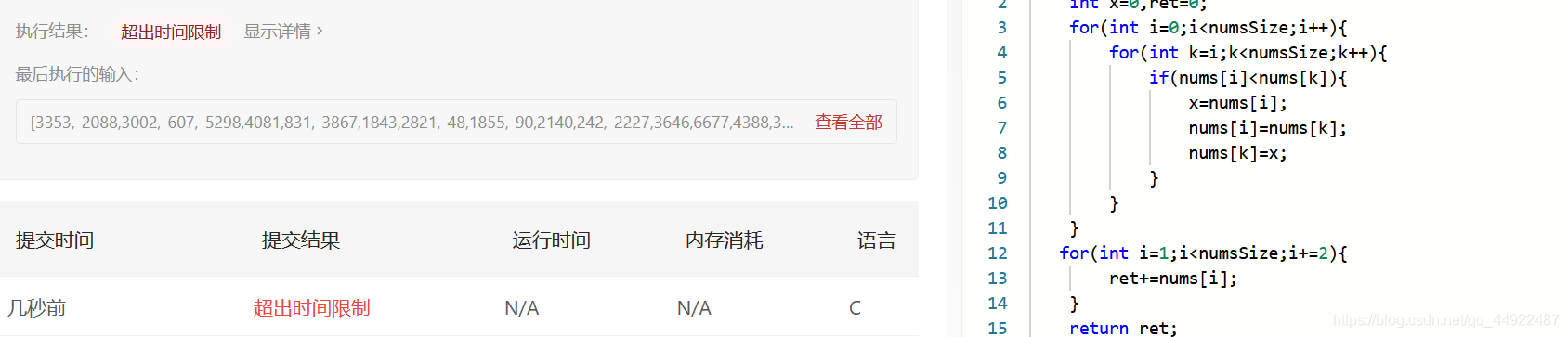
要解决这问题可以使用C语言里的自带的一个数组排序函数qsort()

这里不写具体用法，给个大致的轮廓示意

int compare(const void* a, const void* b) {
    return (*(int*)a)-(*(int*)b);//从小到大
    //return *(int *)b-*(int *)a;//从大到小
}

void func(int* nums, int numsSize) {
    qsort(nums,numsSize,sizeof(int),compare);
}

融合搭配随后的代码里就是这样。

int cmp(int *a, int *b) {
    return *a - *b;
}

int arrayPairSum(int *nums, int numsSize) {
    qsort(nums, numsSize, sizeof(int), cmp);
    int ret = 0;
    for (int i = 0; i < numsSize; i += 2) {
        ret += nums[i];
    }
    return ret;
}

对于再c语言中很多时候借助于已有的函数逻辑来进行编码的确时恒有帮助，日后会再c语言笔记里补充上各大c函数的笔记。