C#中的深度学习（五）：在ML.NET中使用预训练模型进行硬币识别

在本系列的最后，我们将介绍另一种方法，即利用一个预先训练好的CNN来解决我们一直在研究的硬币识别问题。

在这里，我们看一下转移学习，调整预定义的CNN，并使用Model Builder训练我们的硬币识别模型。

我们将使用ML.NET代替Keras.NET。为什么不使用Keras.NET呢?尽管Keras.NET非常简单，易于学习，虽然它包含前面提到的预定义模型，但它的简单性使我们无法自定义CNN架构来适应我们的问题。

ML.NET是一个微软的免费机器学习框架，旨在使用C#和F#进行开发。最重要的是，我们可以将ML.NET与Azure结合使用，这意味着我们可以使用基于云的基础设施来训练我们的模型。让多个虚拟机以分布式方式运行我们的代码可以使训练更快、更准确。

为什么预训练的CNN如此有价值?因为有人花了很多时间和资源培训他们，我们可以利用这一点。我们可以重用嵌入在为网络计算的权值，我们可以将它们重新应用到类似的问题中。也就是说，它们不仅可以应用于CNN最初训练解决的问题。这种方法就被称为迁移学习。它可以为我们节省大量的培训时间，并大大提高所获得的结果。

在迁移学习中，我们不像以前那样从零开始。相反，我们从一个已知的模型开始，该模型具有预定义的体系结构和在第一次请求模型时下载的计算权重。流行的模型包括Inception、ResNet和VGG16等。

要针对我们的问题调整预定义的CNN，我们必须做三件事。首先，我们必须将输入层的形状更改为数据集中图像的维度。其次，我们至少需要更改输出层，以便模型拥有与数据集相同数量的类。第三，我们必须调整模型，让它知道我们对训练预定义模型的层不感兴趣。

完成这些步骤后，我们可以训练或使我们的模型适合于给定的数据集。

让我们开始吧。在Visual Studio中，转到Extensions > Manage Extensions，浏览ML.NET Model Builder。

我们还需要安装Nuget包ML.NET。

为了训练我们的模型来解决硬币识别问题，我们将使用 Model Builder 扩展。

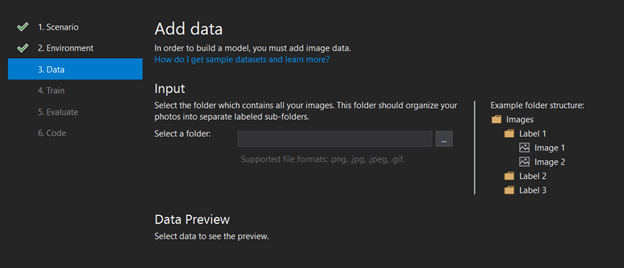
使用这个工具，我们可以轻松地设置数据集并训练模型，它通过 Model Builder中添加的Auto ML特性自动选择模型。自动机器学习(automatic Machine Learning, Auto ML)是一种自动化机器学习模型开发中的耗时任务。所以Model Builder将为我们简化准备数据集的过程，以及选择预先训练好的模型和所有涉及的参数。关于所选的预训练模型，有一点是只有最后一层会被重新训练;其他所有人都保持权重。

对于数据集的情况，唯一的要求是将其组织在文件夹中，这样文件夹名就是其中所有图像的类或标签。

当我们到目前为止使用的硬币数据集被输入到模型构建器中时，AutoML引擎选择ResNet作为预先训练好的架构来用于我们的问题。

一旦训练结束，我们就可以预测新的输入数据，甚至可以得到与为预测而生成的模型相对应的代码。只需这么少的工作，我们就可以在几乎没有任何相关知识的情况下使用ML，通过UI简单地完成所有工作，选择、单击并在最后获得代码。

关于使用C#进行硬币识别的系列文章到此结束。希望你喜欢！如果有任何问题，不要忘记留言或发信息。感谢你的阅读。

欢迎关注我的公众号，如果你有喜欢的外文技术文章，可以通过公众号留言推荐给我。