LOJ10132

在 Adera 的异时空中有一张地图。这张地图上有 N 个点，有 N-1 条双向边把它们连通起来。起初地图上没有任何异象石，在接下来的 M 个时刻中，每个时刻会发生以下三种类型的事件之一：

1. 地图的某个点上出现了异象石（已经出现的不会再次出现）；
2. 地图某个点上的异象石被摧毁（不会摧毁没有异象石的点）；
3. 向玩家询问使所有异象石所在的点连通的边集的总长度最小是多少。

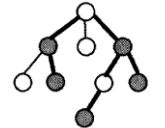
请你作为玩家回答这些问题。下图是一个例子，灰色节点表示出现了异象石，加粗的边表示被选为连通异象石的边集。

输入格式

第一行有一个整数 N，表示点的个数；

接下来 N-1 行每行三个整数 x,y,z，表示点 x 和 y 之间有一条长度为 z 的双向边；

第 N+1 行有一个正整数 M；

接下来 M 行每行是一个事件，事件是以下三种格式之一：

• + x：表示点 x 上出现了异象石；
• - x：表示点 x 上的异象石被摧毁；
• ?：表示询问使当前所有异象石所在的点连通所需的边集的总长度最小是多少。

输出格式

对于每个 ? 事件，输出一个整数表示答案。

样例

样例输入

6
1 2 1
1 3 5
4 1 7
4 5 3
6 4 2
10
+ 3
+ 1
?
+ 6
?
+ 5
?
- 6
- 3
?

样例输出

5
14
17
10

数据范围与提示

对于 30% 的数据，1≤ n,m ≤ 10^3；

对于另 20% 的数据，地图是一条链，或者一朵菊花；

对于 100% 的数据，1≤ n,m ≤ 10^5,1 ≤ x,y ≤ n,x ̸​= y,1 ≤ z ≤ 10^9。

________________________________________________________________________________________

有一个很有趣的结论，把所有的点连接起来的的最短距离刚好是，dfs序中所有选取点相邻两点之间的距离，所以用LCA就可以了。比较麻烦的是选取点的次序，不能暴力，太慢！所以想到了平衡树，太麻烦了。后来看书上说用SET。比赛时不知道会不会挂。

SET用的不熟练，很多是临时查的，所以调了半天！

________________________________________________________________________________________

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 typedef long long ll;
  4 const ll maxn=1e5+10;
  5 struct edge
  6 {
  7     ll u,v,w,nxt;
  8 }e[maxn<<1];
  9 ll head[maxn],js;
 10 ll n,m;
 11 void addage(ll u,ll v,ll w)
 12 {
 13     e[++js].u=u;e[js].v=v;e[js].w=w;
 14     e[js].nxt=head[u];head[u]=js;
 15 }
 16 ll cx[maxn],xh[maxn];
 17 set <ll> s;
 18 ll f[maxn][20],dep[maxn],deps[maxn];
 19 void dfs(ll u,ll fa)
 20 {
 21     dep[u]=dep[fa]+1;
 22     for(ll i=head[u];i;i=e[i].nxt)
 23     {
 24         ll v=e[i].v;
 25         if(v!=fa)
 26         {
 27             f[v][0]=u;deps[v]=deps[u]+e[i].w;
 28             for(int j=1;j<20;++j)
 29             {
 30                 f[v][j]=f[f[v][j-1]][j-1];
 31             }
 32             dfs(v,u);
 33         }
 34     }
 35 }
 36 ll ind;
 37 ll ans;
 38 void dfsf(ll u,ll fa)
 39 {
 40     cx[++ind]=u;xh[u]=ind;
 41     for(int i=head[u];i;i=e[i].nxt)
 42     {
 43         ll v=e[i].v;
 44         if(v!=fa)dfsf(v,u);
 45     }
 46 }
 47 ll lca(ll u,ll v)
 48 {
 49     if(dep[u]<dep[v])swap(u,v);
 50     for(int i=19;i>=0;--i)if(dep[f[u][i]]>=dep[v])u=f[u][i];
 51     if(u==v)return v;
 52     for(int i=19;i>=0;--i)if(f[u][i]!=f[v][i])u=f[u][i],v=f[v][i];
 53     return f[u][0];
 54 }
 55 ll lcaf(ll u,ll v)
 56 {
 57     ll l=lca(u,v);
 58     return deps[u]+deps[v]-deps[l]-deps[l];
 59 }
 60 int main()
 61 {
 62     scanf("%lld",&n);
 63     for(int i=1;i<n;++i)
 64     {
 65         ll u,v,w;
 66         scanf("%lld%lld%lld",&u,&v,&w);
 67         addage(u,v,w);addage(v,u,w);
 68     }
 69     dfs(1,0);
 70     scanf("%lld",&m);
 71     dfsf(1,0);
 72     char ss[3];
 73     int x;
 74     pair<set<ll>::iterator,bool> pr;
 75     set<ll>::iterator it,it2,tp;
 76     while(m--)
 77     {
 78         scanf("%s",ss);
 79         if(ss[0]=='+')
 80         {
 81             scanf("%d",&x);
 82             if(s.size()==0)
 83             {
 84                 s.insert(xh[x]);
 85                 continue;
 86             }
 87             it=s.lower_bound(xh[x]);it2=it;
 88             if(it==s.end())it=s.begin();
 89             if(it2==s.begin()){it2=s.end();it2--;}else it2--;
 90             ans+=lcaf(cx[*it],x)+lcaf(x,cx[*it2])-lcaf(cx[*it],cx[*it2]);
 91             s.insert(xh[x]);
 92         }
 93         else if(ss[0]=='-')
 94         {
 95             scanf("%d",&x);
 96             tp=s.end();tp--;
 97             it=s.lower_bound(xh[x]);it2=it;
 98             if(it==tp)it=s.begin();else it++;
 99             if(it2==s.begin())it2=tp;else it2--;
100             ans+=lcaf(cx[*it],cx[*it2])-lcaf(x,cx[*it])-lcaf(x,cx[*it2]);
101             s.erase(xh[x]);
102         }
103         else
104         {
105             printf("%lld\n",ans/2);
106         }
107     }
108     return 0;
109 }