数据分析First week（7.15~7.21）

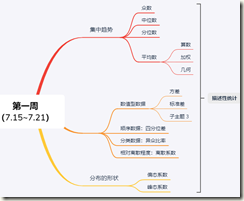
描述统计学

当我们面对大量信息的时候，经常会出现数据越多，事实越模糊的情况，因此我们需要对数据进行简化，描述统计学就是用几个关键的数字来描述数据集的整体情况。

1.集中趋势

1.1 众数

众数是样本观测值在频数分布表中频数最多的那一组的组中值

当众数不止一个时，可以用众数指定具有最高频数的数值组，被称为众数组。

求众数三步法：

① 把数据中的不同类别或数值全部找出来

② 写出每个数值或类别的频数

③ 挑出具有最高频数的一个或几个数值，得出众数。

用众数代表一组数据，可靠性较差，不过，众数不受极端数据的影响，并且求法简便。

在一组数据中，如果个别数据有很大的变动，选择中位数表示这组数据的“集中趋势”就比较适合。

1.2 中位数

当异常值使平均值产生误导时，我们需要使用其他方式表示典型值，我们可以取中位数。

求中位数三步法：

① 从小到大按顺序排列数字

② 如果有奇数个数值，则中位数位于中间的数值。如果有n个数，则中间数的位置为（n+1）/ 2

③ 如果有偶数个数值，则将两个中间数相加，然后除以2。中间位置的算法是（n+1）/2，两个中间数分别位于这两个中间位置的两侧

中位数永远处于中间，它是个中间值。但是碰到数据较多的数据集时，计算中位数相对会比较麻烦

1.3 分位数

分位数指的就是连续分布函数中的一个点，这个点对应概率p。若概率0<p<1，随机变量X或它的概率分布的分位数Y，是指满足条件p(X≤Y )=α的实数。

常用的有中位数（即二分位数）、四分位数、百分位数等。下面介绍下四分位数，

四分位数（Quartile）是统计学中分位数的一种，即把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分位数。

1）第一四分位数(Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字；

2）第二四分位数(Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字；

3）第三四分位数(Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

第三四分位数与第一四分位数的差距又称四分位距。

1.4 平均数

平均数是统计学中最常用的统计量，用来表明资料中各观测值相对集中较多的中心位置。

算数平均数

算术平均数是指在一组数据中所有数据之和再除以数据的个数。它是反映数据集中趋势的一项指标。

把n个数的总和除以n，所得的商叫做这n个数的算术平均数。

加权平均数

加权平均值即将各数值乘以相应的权数，然后加总求和得到总体值，再除以总的单位数。

加权平均值的大小不仅取决于总体中各单位的数值（变量值）的大小，而且取决于各数值出现的次数（频数），由于各数值出现的次数对其在平均数中的影响起着权衡轻重的作用，因此叫做权数。

若n个数的权分别是 那么 做这n个数的加权平均值。

几何平均数

n个观察值连乘积的n次方根就是几何平均数。根据资料的条件不同，几何平均数分为加权和不加权之分。

1) 简单几何平均

2）加权几何平均

特点：

1、几何平均数受极端值的影响较算术平均数小；

2、如果变量值有负值，计算出的几何平均数就会成为负数或虚数；

3、它仅适用于具有等比或近似等比关系的数据；

4、几何平均数的对数是各变量值对数的算术平均数。

2.离中趋势

2.1 数值型数据

方差

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数.

总体方差计算公式：

为总体方差， 为变量， 为总体均值， 为总体例数

但在实际应用中，总体均数难以得到时，应用样本统计量代替总体参数，有样本方差：

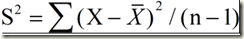
为样本方差，X为变量， 为样本均值，n为样本例数.

在概率分布中，设X是一个离散型随机变量，若E{[X-E（X）]^2}存在，则称E{[X-E（X）]^2}为X的方差，记为D（X）或Var（X），其中E（X）是X的期望值，X是变量值。在应用上引入量 ，称为标准差或均方差.

标准差

标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根.它反映组内个体间的离散程度.

标准差与平均值定义公式：

标准差表示的就是样本数据的离散程度。标准差就是样本平均数方差的开平方，标准差通常是相对于样本数据的平均值而定的，通常用M±SD来表示，表示样本某个数据观察值相距平均值有多远。从这里可以看到，标准差受到极值的影响。标准差越小，表明数据越聚集；标准差越大，表明数据越离散.

极差

极差又称范围误差或全距(Range)，以R表示，是用来表示统计资料中的变异量数(measures of variation)，其最大值与最小值之间的差距，即最大值减最小值后所得之数据.

计算方式 :最直接也是最简单的方法，即最大值－最小值（也就是极差）来评价一组数据的离散度。例如比赛中去掉最高最低分就是极差的具体应用。

在统计中常用极差来刻画一组数据的离散程度，以及反映的是变量分布的变异范围和离散幅度，在总体中任何两个单位的标准值之差都不能超过极差。同时，它能体现一组数据波动的范围。极差越大，离散程度越大，反之，离散程度越小。

2.2 顺序数据--四分位差

前面已经介绍过四分位数，四分位差（quartile deviation），就是上四分位数（Q3）与下四分位数（Q1）的差。

计算公式为：Q = Q3-Q1

四分位差反映了中间50%数据的离散程度，其数值越小，说明中间的数据越集中；其数值越大，说明中间的数据越分散。四分位差不受极值的影响。此外，由于中位数处于数据的中间位置，因此，四分位差的大小在一定程度上也说明了中位数对一组数据的代表程度。四分位差主要用于测度顺序数据的离散程度。对于数值型数据也可以计算四分位差，但不适合分类数据。

2.3 分类数据--异众比率

异众比率指的是总体中非众数次数与总体全部次数之比。换句话说，异众比率指非众数组的频数占总频数的比例。

计算公式1 ：

其中
表示异众比率，
为变量值的总频数；
为众数组的频数 ，m表示数组的数量。

计算公式2：

其中， 表示异众比率，
表示众数次数，N表示总体单位总数（即总体次数）。

异众比率主要适合测度分类数据的离散程度，当然，对于顺序的数据以及数值型数据也可以计算异众比率.

异众比率主要用于衡量众数对一组数据的代表程度。异众比率越大，说明非众数组的频数占总频数的比重越大，众数的代表性就越差；异众比率越小，说明非众数组的频数占总频数的比重越小，众数的代表性越好.

2.4 相对离散程度--离散系数

离散系数是衡量资料中各观测值离散程度的一个统计量。当进行两个或多个资料离散程度的比较时，如果度量单位与平均数相同，可以直接利用标准差来比较。如果单位和（或）平均数不同时，比较其离散程度就不能采用标准差，而需采用标准差与平均数的比值（相对值）来比较 ：

表示总体离散系数和样本离散系数.

离散系数通常可以进行多个总体的对比，通过离散系数大小的比较可以说明不同总体平均指标（一般来说是平均数）的代表性或稳定性大小。一般来说，离散系数越小，说明平均指标的代表性越好；离散系数越大，平均指标的代表性越差.

1.优点

比起标准差来，离散系数的好处是不需要参照数据的平均值。离散系数是一个无量纲量，因此在比较两组量纲不同或均值不同的数据时，应该用变异系数而不是标准差来作为比较的参考。

2.缺点

• 当平均值接近于0的时候，微小的扰动也会对离散系数产生巨大影响，因此造成精确度不足。
• 离散系数无法发展出类似于均值的置信区间的工具

3 分布的形状

3.1 偏态系数

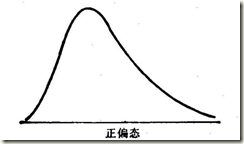
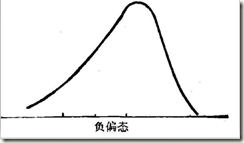
偏态系数以平均值与中位数之差对标准差之比率来衡量偏斜的程度，用SK表示偏斜系数:偏态系数小于0，因为平均数在众数之左，是一种左偏的分布，又称为负偏。偏态系数大于0，因为均值在众数之右，是一种右偏的分布，又称为正偏。

偏态系数是根据众数、中位数与均值各自的性质，通过比较众数或中位数与均值来衡量偏斜度的，即偏态系数是对分布偏斜方向和程度的刻画.

简单偏态系数

计算公式为：

加权偏态系数

计算公式为： 

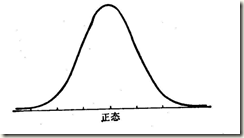
零值：偏态系数的取值为0时，表示数据为完全的对称分布，即正态分布。正值：偏态系数的取值为正数时，表示数据为正偏态或右偏态。负值：偏态系数的取值为负数时，表示数据为负偏态，或左偏态。

3.2 峰态系数

峰态系数( kurtosis)即“峰度”。是用来反映频数分布曲线顶端尖峭或扁平程度的指标.
计算公式：

峰度系数用来度量数据在中心聚集程度。在正态分布情况下，峰度系数值是3（但是SPSS等软件中将正态分布峰度值定为0，是因为已经减去3，这样比较起来方）.大于3的峰度系数说明观察量更集中，有比正态分布更短的尾部；小于3的峰度系数说明观测量不那么集中，有比正态分布更长的尾部，类似于矩形的均匀分布。峰度系数的标准误用来判断分布的正态性。峰度系数与其标准误的比值用来检验正态性。如果该比值绝对值大于2，将拒绝正态性。

在金融中，若某分布与正态分布有相同的方差，但是峰度系数大于3，则呈现“尖峰厚尾”形态，峰度更高，两段的尾部更厚，也就是极值更多的意思。

自言自语

有幸遇到居士，能和那么多伙伴一起学习，感谢为我们解答疑惑的大佬们！！

第一周，由于自己没安排好时间，做的总结也不怎么样，只有一些理论，并没有实际操作，争取下一周用Python写出来。

感谢遇见 ，继续加油！