LR Optimization-Based Estimator Design for Vision-Aided Inertial Navigation

Abstract

我们设计了一个 hybrid 估计器, 组合了两种算法, sliding-window EKF 和 EKF-SLAM.

我们的结果表示, hybrid算法比单一的好.

1. Introduction

EKF-SLAM和sliding-window EKF对相同的测量信息以不同的处理.

我们展示说, 最优的处理方式是, 基于特征跟踪长度 的分布来处理每个特征.

这个分布不是事先知道的(它基于环境, 相机运动), 所以我们从图像序列中学习. 使用了这个信息, 最优的策略来处理特征测量可以通过解决一个 单变量优化问题 来解决.

2. Related Work

a) Exact Reformulations of the SLAM equation

b) Approximations of the SLAM equations

[5-7] 用了SLAM等式的近似来减少计算量, 我们的方法没有写信息丢失, 没有近似, 比起EKF的线性化的不准确.

c) Feature Selection methods

3. Estimators for VIO

MSCKF和EKF-SLAM都用了一样的信息, 只是用不同的方法来组织算力和线性化.

如果测量模型是线性的, 两个方法会有一样的结果,跟IMU位姿的MAP是一样的.

在算力上, 就很不一样了. EKF-SLAM的算力是特征数量的立方(因为在状态向量里, 所有特征是可观的), 而MSCKF是跟特征数量线性的, 而跟特征跟踪的长度立方.

所以,

如果很多特征被跟踪, 即使是在很小的帧中, MSCKF会更好.
如果有很多点被长期跟踪, EKF-SLAM会计算力更低

所以EKF-SLAM和MSCKF是互补的.

4. The Hybrid MSCKF/SLAM Algorithm

A. The MSCKF algorithm for VIO

特征向量:

\[\mathbf{x}_{k}^{T}=\left[\begin{array}{lllll}
\mathbf{x}_{I_{k}}^{T} & \mathbf{x}_{C_{1}}^{T} & \mathbf{x}_{C_{2}}^{T} & \cdots & \mathbf{x}_{C_{m}}^{T}
\end{array}\right]^{T}
\]

IMU的状态是:

\[\mathbf{x}_{I}=\left[\begin{array}{lllll}
\overline{\mathbf{q}}^{T} & \mathbf{p}^{T} & \mathbf{v}^{T} & \mathbf{b}_{g}^{T} & \mathbf{b}_{a}^{T}
\end{array}\right]^{T}
\]

MSCKF用IMU测量来传播当前的IMU状态和协方差矩阵, $P_{k+1|k}$.

我们假设第 $i-th$个特征, 它在 $l$ 个图像被观测到, 然后刚跟踪失效. 这时候, 我们用所有的特征测量来做EKF更新.

观测的非线性等式是: $z_{ij} = h(x_{C_j}, f_i) + n_{ij}$ , for ${h = 1, ..., l}$, $f_i$ 是特征的位置(逆深度表示); $n_{ij} $ 是噪声向量, 零均值高斯, cov是$\sigma^2 \mathbf{I}_2$.

使用所有的观测, 我们计算特征观测 $\hat{f}_i$ , 然后计算残差 $\tilde{z}_{ij} = z_{ij}- h(\hat{x}_{C_j}, \hat{f}_i), j= 1 ... l$. 通过线性化, 这些残差可以被写为:

\[\tilde{\mathbf{z}}_{i j} \simeq \mathbf{H}_{i j} \tilde{\mathbf{x}}_{C_{i}}+\mathbf{H}_{f_{i j} \mathbf{f}_{i}}+\mathbf{n}_{i j}, j=1 \ldots \ell
\]

因为特征没有被包括在MSCKF的状态向量里, 我们把它边缘化掉.

首先, 我们形成这个 $l$ 个残差(一个地图点的所有观测):

\[\tilde{\mathbf{z}}_{i} \simeq \mathbf{H}_{i} \tilde{\mathbf{x}}+\mathbf{H}_{f_{i}} \tilde{\mathbf{f}}_{i}+\mathbf{n}_{i}
\]

这里 $\tilde {z}_i$ 和 $n_i$ 是元素 $\tilde{z}_{ij}$ 和 $n_{ij}$ 组成.

我们定义残差向量 $\tilde{z}^o_i = V^T \tilde{z}_i$, 这里 $V$ 是一个列形成 $H_{fi}$ 左零空间 (left nullspace) 的矩阵. 所以, 我们有:

\[\tilde{\mathbf{z}}_{i}^{o}=\mathbf{V}^{T} \tilde{\mathbf{z}}_{i} \simeq \mathbf{V}^{T} \mathbf{H}_{i} \tilde{\mathbf{x}}+\mathbf{V}^{T} \mathbf{n}_{i}=\mathbf{H}_{i}^{o} \tilde{\mathbf{x}}+\mathbf{n}_{i}^{o}\tag{5}
\]

然后, 我们可以用马氏gating test, 对于残差 $\tilde{z}^o_i$:

\[\gamma=\left(\tilde{\mathbf{z}}_{i}^{o}\right)^{T}\left(\mathbf{H}_{i}^{o} \mathbf{P}_{k+1 \mid k}\left(\mathbf{H}_{i}^{o}\right)^{T}+\sigma^{2} \mathbf{I}\right)^{-1} \tilde{\mathbf{z}}_{i}^{o}
\]

通过把所有的残差堆叠在一起, 我们有:

\[\tilde{z}^o = H^o\tilde{x} +n^o
\]

如果在某个时刻有很多特征要处理, 可以省略更多的计算资源. 在[10]中, 我们可以计算 $H^o$ 的QR分解, 写作 $H^o=QH^r$, 然后用 $\tilde{z}^r$ 来更新:

\[\tilde{\mathbf{z}}^{r}=\mathbf{Q}^{T} \tilde{\mathbf{z}}^{o}=\mathbf{H}^{r} \tilde{\mathbf{x}}+\mathbf{n}^{r}\tag{8}
\]

这里 $n^r$ 是一个 $r\times1$ 的噪声向量, 协方差矩阵 $\sigma^2 \mathbf{I}_r$.

一旦 $\tilde{z}^r$ 和矩阵 $H^R$ 被计算了, 我们计算state correction 和 update covariance矩阵通过标准的EKF公式:

\[\begin{aligned}
\Delta \mathbf{x} &=\mathbf{K} \tilde{\mathbf{z}}^{r} \\
\mathbf{P}_{k+1 \mid k+1} &=\mathbf{P}_{k+1 \mid k}-\mathbf{K} \mathbf{S} \mathbf{K}^{T} \\
\mathbf{S} &=\mathbf{H}^{r} \mathbf{P}_{k+1 \mid k}\left(\mathbf{H}^{r}\right)^{T}+\sigma^{2} \mathbf{I}_{r} \\
\mathbf{K} &=\mathbf{P}_{k+1 \mid k}\left(\mathbf{H}^{r}\right)^{T} \mathbf{S}^{-1}
\end{aligned}
\]

B. Computational complexity of the MSCKF

MSCKF计算特征观察的方式是最优的, 因为除了EKF的线性化[22]之外, 没有用任何近似.

这个在滑窗的状态 $m$ , 包含最少最长的特征跟踪的状态.

如果不是的话, 那么大于 $m$ 过去的观测就没法被处理了. 所以为了利用所有可用的特征, MSCKF必须保持一个足够长的滑窗的状态.

MSCKF的计算量以如下决定:

Eq 5计算的残差和雅克比矩阵. 如果有 $n$ 个特征要处理, 特征跟踪的长度是 $l_i$, 那就需要 $\mathcal{O}(\Sigma_{i=1}^n \mathcal{l}^3_i)$ 个操作.
马氏测试, 需要 $\mathcal{O}(\Sigma_{i=1}^nl^3)$ 个操作.
Eq 8中的计算, 大约是 $\mathcal{O}(\Sigma_{i=1}^nl^3)$个操作
卡尔曼增益和协方差更新的计算, 需要 $\mathcal{O}\left(r^{3} / 6+r(15+6 m)^{2}\right)$ . 这里 $15+6m$ 是状态协方差的大小, $r$ 是 $H^r$ 个行数.

\[r=2(l_{(1)}+l_{(2)}+l_{(3)})-7\tag{13}
\]

这里 l _1,2,3 是三个最长的特征跟踪.

C. The hybrid MSCKF/SLAM algorithm

我们的状态向量是, 有IMU状态, 滑窗的m个相机, 和$s_k$ 个特征.

\[\mathbf{x}_{k}=\left[\begin{array}{ccccccc}
\mathbf{x}_{I_{k}}^{T} & \mathbf{x}_{C_{1}}^{T} & \cdots & \mathbf{x}_{C_{m}}^{T} & \mathbf{f}_{1}^{T} & \cdots & \mathbf{f}_{s_{k}}^{T}
\end{array}\right]^{T}
\]

最优的(考虑计算需求)策略来用特征是简单的:

如果特征的track数少于 $m$, (i.e. $l_i < m$), 那么用MSCKF来处理.
如果大于$m$ 个track, 就初始化到state vector.

\[\tilde{\mathbf{z}}_{k}=\left[\begin{array}{c}
\tilde{\mathbf{z}}_{k}^{r} \\
\tilde{\mathbf{z}}_{1 m} \\
\vdots \\
\tilde{\mathbf{z}}_{s_{k} m}
\end{array}\right] \simeq\left[\begin{array}{c}
\mathbf{H}^{r} \\
\mathbf{H}_{1 m} \\
\vdots \\
\mathbf{H}_{s_{k} m}
\end{array}\right] \tilde{\mathbf{x}}_{k}+\mathbf{n}_{k}=\mathbf{H}_{k} \tilde{\mathbf{x}}_{k}+\mathbf{n}_{k}
\]

在上式中, $\tilde{z}_{jm}$ 是 $s_k$ SLAM特征的残差观测, $H_{jm}$ 是相关的雅克比. 每个残差是一个 $2\times1$ 的向量, $H_{jm}$ 是一个 $2\times(15+6m+3s_k)$ 的矩阵.

为了初始化新的特征, $m$ 个观测会用来三角化 然后计算它的初始协方差 和 跟其他滤波状态的互相关.

我们用逆深度, 因为它很棒的线性化特性. 最新的相机clone, $x_{C_m}$ 是用作"anchor" state.

5. 优化Hybrid EKF的表现

$m$ 的选择有一个深渊的影响在算法的视觉需要上.

A. Operation count for each update

每个迭代的浮点运算的数量:

\[\begin{aligned}
f_{k}=& \alpha_{1} \sum_{i=1}^{n} \ell_{i}^{3}+\alpha_{2}\left(r+2 s_{k}\right)^{3} \\
&+\alpha_{3}\left(r+2 s_{k}\right)\left(15+6 m+3 s_{k}\right)^{2}+l . o . t
\end{aligned}\tag{16}
\]

$\alpha_i$ 是已知常量, $n$ 是MSCKF的特征数, $r$ 是Eq13, $l.o.t.$ 表示lower order terms.

上式的三个项对应MSCKF残差的计算, 矩阵 $\mathbf{S}$ 的Cholesky factorization, 和协方差的更新等式.

$r$ 表示约束的个数, it is bounded above by $6m-7$: 滑窗中的位置量是 $6m$, 特征估计不能提供任何全局pose和scale的信息, 也就是7个自由度; 如果有很多特征, 我们有$r \approx 6m-7 $:

\[\begin{aligned}
f_{k} \approx & \alpha_{1} \sum_{i=1}^{n} \ell_{i}^{3}+\alpha_{2}\left(6 m+2 s_{k}-7\right)^{3} \\
&+\alpha_{3}\left(6 m+2 s_{k}-7\right)\left(15+6 m+3 s_{k}\right)^{2}
\end{aligned}
\]

B. Minimizing the average operation count

我们现在来决定 $m$ 的最优值, 来最小化 hybrid EKF的时间.

Eq 16提供了一次滤波更新计算的操作数. 第一眼看的时候, 我们可能会觉得是根据 $m$ 来最小化公式. 但是实际是一个病态的问题. 举例, 如果$m=20$ , 这时候有10个特征有20个track; 这时候我们可以选择提升window size或者是加到state vector. 但是最优解是基于未来的行为的, 如果有>>20个track, 自然是加到状态里好. 如果只有21个track, 自然increase $m$ 是更好的做法.

我们可以用统计数据. 在滤波操作的时候, 我们收集数据来学习probability mass function(pmf) 在特征跟踪长度上 $p(l_i)$. 用pmfs, 我们可以计算平均下来EKF更新的操作数 $\bar{f}(m)$.

我们发现这个cost curve是 quasiconvix(准凸面).

所以, 为了减少优化需要的时间, 我们从一个足够好的初始猜测(e.g. the last computed threshold)通过局部搜索来做优化. 因为特征track的数据特征会会随着时间改变, 我们在15秒的区间做pmf的学习.

注意在现代电脑, flop计算来model计算量的cost不一定是永远work的, 因为表现还会被一些因素影响, 比如: vectorization, cache access patterns, data locality, etc.

6. Experimental Results

我们基于数据集[26]来做测试, 有29.6km长的轨迹.

**我们发现纯MSCKF得到最高的精度. 我们把这个归因于两个原因: 1. MSCKF特征都显式的边缘化了, 也没有Gaussianity假设给pdf在特征位置误差上(在SLAM里是这么做的). 2. 特征的所有测量都在MSCKF里联合用了, 这样外点会被更容易的检测, 也可以计算更好的线性点. ** ???

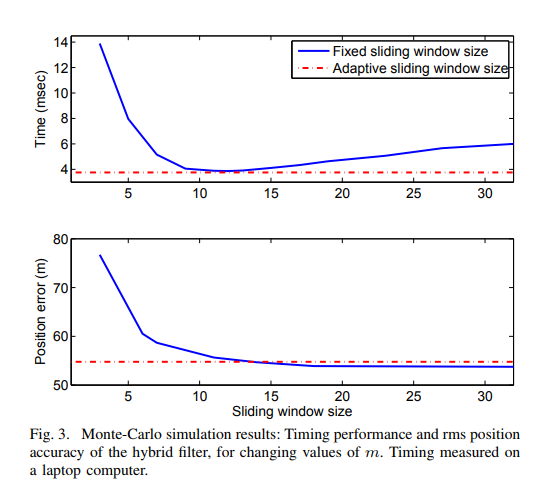
通过融合MSCKF和EKF-SLAM, 可能丢失了一些精度, 因为在状态向量里的特征被假设是Gaussian的. 但是, 我们可以看到, 如果window的size大于一个值(比如9), 精度的变化就可以忽略不计了.

这个insight是, 如果有足够数量的观测来初始化特征, 那么特征的errors'pdf就变得"足够高斯", 这样hybrid filter的精度就跟MSCKF很接近了, 在我们的优化中, 我们不允许 $m$ 的值比一个阈值(7)小.

Fig. 3的时间损耗是在Core i7(2.13 GHz)上算的. 如果在这个平台上, 是很容易实时的, hybrid filter需要4msec之内(在最优的值 $m$ 的时候).

B. Real-world data

每帧平均track 540个特征点, 平均track长度是5.06帧.

在移动处理器上跑的时候, MSCKF平均更新时间是139ms, EKF是774ms, hybrid是77ms.

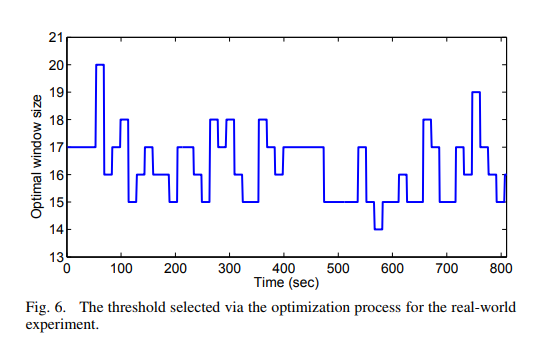
我们每15秒计算一次, 这个过程要0.31ms.

7. Discussion and Concluding Remarks

没啥