P2585 三色二叉树 题解

题目

一棵二叉树可以按照如下规则表示成一个由0、1、2组成的字符序列，我们称之为"二叉树序列S"：

\[S=\left\{
\begin{aligned}
0 &\ \ 表示该树没有子节点 \\
1S_1 &\ \ 表示该树有一个子节点,S_1为其子树的二叉树序列 \\
2S_1S_2 &\ \ 表示该树有两个子节点,S_1和S_2分别表示其两个子树的二叉树序列
\end{aligned}
\right.
\]

例如，下图所表示的二叉树可以用二叉树序列S=21200110来表示:

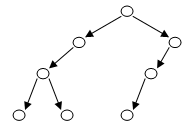
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且，一个节点与其子节点的颜色必须不同，如果该节点有两个子节点，那么这两个子节点的颜色也必须不相同。给定一棵二叉树的二叉树序列，请求出这棵树中最多和最少有多少个点能够被染成绿色

输入格式

输入文件仅有一行，不超过\(5\times 10^5\)个字符，表示一个二叉树序列

输出格式

输出文件也只有一行，包含两个数，依次表示最多和最少有多少个点能够被染成绿色

输入样例

1122002010

输出样例

5 2

题解

直接用输入DFS来树形DP.

定义maxv和minv两个数组,maxv[i][j]表示以\(i\)号节点为根节点的子树最多能染成绿色的节点数量,当\(j=0\),根节点被染成绿色;当\(j=1\),根节点被染成红色;当\(j=2\),根节点被染成蓝色.

minv类似,代表最少能染成绿色的节点数量.

当根节点有一个子节点时,这个子节点不能和根节点一个颜色,所以从剩下的两种颜色中挑选最大的更新.注意当根节点为绿色时,dp值需要加1(多了根节点一个绿色节点)

当根节点有两个子节点时,这两个子节点不能和根节点一个颜色,而又只剩下两种颜色,所以有两种情况,从这两种情况中选最大的更新即可.同样注意当根节点为绿色时的情况.

那么,怎么DFS这一个特殊序列?

首先可以确定的是,根节点就是第一项,那么通过第一项可以得知根节点有几个子树,如果这棵树不为空,那么左子树的根节点一定是第二项,注意如果只有一棵子树,那么我把唯一的一棵子树看作左子树.

再对左子树进行相同的递归操作,遇到0回溯,因为保证叶节点一定为0,所以不需要检查边界,回溯的时候,可以返回这棵子树在序列中最后一项的位置,这个位置加一就是右子树(如果有两棵子树).

以此类推,就能在不建树的情况下DFS它

代码

#include <iostream>
#include <string>
using namespace std;
const int maxn = 10005;
string s;
int maxv[maxn][3], minv[maxn][3];
int dfs(int root) {
    if (s[root] == '0') {
        maxv[root][0] = minv[root][0] = 1;  // 因为叶节点没有子树,所以若该叶节点不为绿色,这棵子树中绿色节点的个数为0,反之为1
        return root;  // 这棵子树的结尾坐标
    }
    int lend = dfs(root + 1);  // 递归左子树
    if (s[root] == '1') {
        maxv[root][0] = max(maxv[root+1][1],maxv[root+1][2])+1;  // 这个是绿色的,需要额外算上根节点
        maxv[root][1] = max(maxv[root+1][0],maxv[root+1][2]);  // 这两种代表什么颜色其实无关紧要
        maxv[root][2] = max(maxv[root+1][0],maxv[root+1][1]);
        minv[root][0] = min(minv[root+1][1],minv[root+1][2])+1;
        minv[root][1] = min(minv[root+1][0],minv[root+1][2]);
        minv[root][2] = min(minv[root+1][0],minv[root+1][1]);
        return lend; // 如果有一棵子树,左子树的结尾就是这棵子树的结尾
    } else {
        int rend = dfs(lend + 1); // 根据左子树的结尾递归右子树
        maxv[root][0] = max(maxv[root+1][1]+maxv[lend+1][2],maxv[root+1][2]+maxv[lend+1][1])+1;
        maxv[root][1] = max(maxv[root+1][0]+maxv[lend+1][2],maxv[root+1][2]+maxv[lend+1][0]);
        maxv[root][2] = max(maxv[root+1][0]+maxv[lend+1][1],maxv[root+1][1]+maxv[lend+1][0]);
        minv[root][0] = min(minv[root+1][1]+minv[lend+1][2],minv[root+1][2]+minv[lend+1][1])+1;
        minv[root][1] = min(minv[root+1][0]+minv[lend+1][2],minv[root+1][2]+minv[lend+1][0]);
        minv[root][2] = min(minv[root+1][0]+minv[lend+1][1],minv[root+1][1]+minv[lend+1][0]);
        return rend;  // 如果有两棵子树,右子树的结尾才是这棵子树的结尾
    }
}
int main() {
    cin >> s;
    dfs(0);
    // 三种情况选最大/最小
    cout<<max(maxv[0][0], max(maxv[0][1], maxv[0][2]))<<" "<<min(minv[0][0], min(minv[0][1], minv[0][2]))<<endl;
    return 0;
}

P.S.

最近记忆力有点下降,这道题在两个网站上的数据范围不同,我照着第一个写,交到第二个上面,疯狂RE,死盯了半个小时也没找到原因...