B-Tree 学习

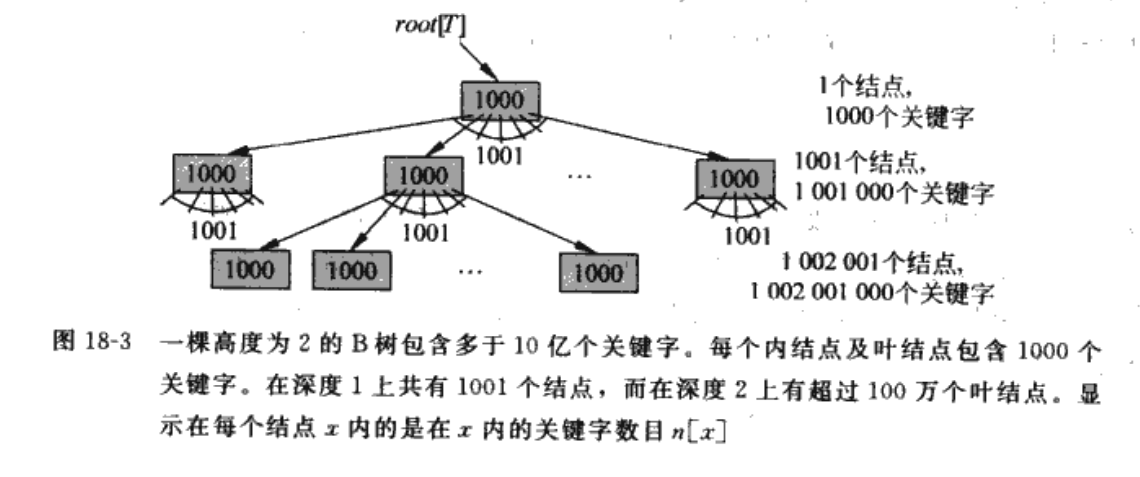
算法导论 第18章 B树
与其他树的结构不同的是  B数是多叉而不是二叉树 而且分叉因子很大
一般使用于数据库 针对需要硬盘IO的情况而使用 可以降低磁盘IO
B树的一个节点是以磁盘的页面为单位，而不是数据内容为单位 一般一个节点等于一个完整的磁盘页

以下B树性质是本人理解  具体定义可查阅算法导论18章节
除了根节点以外 所有节点拥有T-1个 到 2T-1个关键字
关键字升序或者降序排列
节点拥有T个到2T个指针 指向子节点 定义为子节点
若节点仅拥有关键字而无指针 为叶子节点 在树的最下端
T=2时候 树拥有2、3或者4个子节点 成为2-3-4树

以下为我学习的一个简单代码 确定了B树的结构和创建、查找功能 打印节点数值功能。

增删功能比较麻烦，后继增加

// 1213.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>
#include <list>
#include <vector>
#include <assert.h>
using namespace std;

#define t 2;

struct MyB_Tree {
	size_t  keySize_;
	bool    isLeaf_;
	std::vector<size_t>          keys_;
	std::vector<MyB_Tree*>    subTrees_;
	MyB_Tree() {
		keySize_ = 0;
		isLeaf_ = true;
	}
};

struct SearchResult {
	MyB_Tree*   pBTree_;
	size_t      keyNum_;
	SearchResult() {
		pBTree_ = NULL;
		keyNum_ = 0;
	}
	SearchResult(MyB_Tree* pBTree, size_t keyNum) {
		pBTree_ = pBTree;
		keyNum_ = keyNum;
	}
};

MyB_Tree* CreateB_TreeNode() {
	MyB_Tree* pBTree = new MyB_Tree();
	return pBTree;
}

bool BTreeeSearch(MyB_Tree* pBTree, size_t value, SearchResult& result) {
	bool ret = false;
	size_t i = 0;
	while (i <pBTree->keySize_ && value >  pBTree->keys_[i]) {
		i++;
	}
	if (i <pBTree->keySize_ && value == pBTree->keys_[i])
	{
		result.pBTree_ = pBTree;
		result.keyNum_ = i;
		ret = true;
		return ret;
	}
	if (pBTree->isLeaf_) {
		return ret;
	}
	else {
		return BTreeeSearch(pBTree->subTrees_[i], value, result);
	}
}

void PrintTree(MyB_Tree* p) {
	std::cout << "//==========================\nstart print keys : ";
	for (int i = 0; i<p->keySize_; i++) {
		std::cout << p->keys_[i] << " ";
	}

	std::cout << "\n//==========================" << std::endl;
	if (!p->isLeaf_) {
		for (int i = 0; i <= p->keySize_; i++)
		{
			PrintTree(p->subTrees_[i]);
		}
	}
}

int main(int argc, char *argv[])
{
	MyB_Tree* root = CreateB_TreeNode();
	MyB_Tree* subright = CreateB_TreeNode();
	MyB_Tree* subleft = CreateB_TreeNode();

	root->keySize_ = 1;
	root->keys_.push_back(20);

	subleft->keySize_ = 2;
	subleft->keys_.push_back(10);
	subleft->keys_.push_back(19);

	subright->keySize_ = 3;
	subright->keys_.push_back(21);
	subright->keys_.push_back(25);
	subright->keys_.push_back(30);

	root->isLeaf_ = false;
	root->subTrees_.push_back(subleft);
	root->subTrees_.push_back(subright);

	PrintTree(root);

	SearchResult result;
	assert(BTreeeSearch(root, 33, result) == false);
	assert(BTreeeSearch(root, 25, result) == true);
	assert(result.pBTree_ == subright);
	assert(result.keyNum_ == 1);

	std::cout << "finished " << std::endl;
	return 0;
}

运行截图

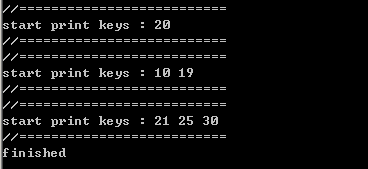
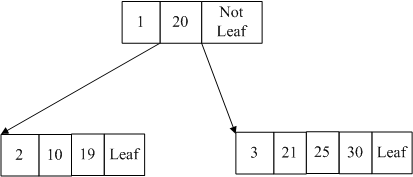
代码建立了一个B树

结构如下